НОУ ИНТУИТ | Математические методы распознавания образов. Лекция 12: Обучение по прецедентам (по Вапнику, Червоненкису)

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Опубликован: 30.04.2008 | Уровень: специалист | Доступ: платный | ВУЗ: Московский государственный университет имени М.В.Ломоносова

|

Вам нравится? Нравится 22 студентам

| Поделиться |

Поддержать программу

Аннотация: Материалы данной лекции включают в себя обучение по прецедентам (по Вапнику, Червоненкису), а также основные теоремы и определения, применимые для классификаторов

12.1. Задача построения классификатора

Пусть

$\Omega$ – пространство образов,
– признаковое пространство,
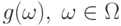$g(\omega),\;\omega\in\Omega$ – индикаторная функция,
– множество признаков.

Тогда 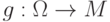$g:\Omega\rightarrow M$ .

Пусть также

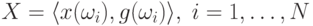$X=\langle x(\omega_i),g(\omega_i)\rangle,\;i=1,\ldots,N$ – множество прецедентов,
$\widehat{g}(x)$ – решающее правило.

Тогда $\widehat{g}:X\rightarrow M$

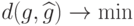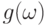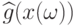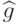Выбор решающего правила исходит из минимизации $d(g,\widehat{g})\rightarrow\min$ , где – метрика, мера близости функций $g(\omega)$ и $\widehat{g}(x(\omega))$ . Построение $\widehat{g}$ называют задачей обучения. 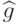$\widehat{g}$ – это ученик, процедура формирования – это учитель, прецеденты – это обучающая последовательность.

12.2. Качество обучения классификатора

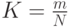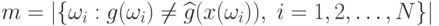Относительная доля несовпадений классификации с учителем для решающего правила есть: $K=\frac{m}{N}$ , где $m=|\{\omega_i:g(\omega_i)\neq\widehat{g}(x(\omega_i)),\;i=1,2,\ldots,N\}|$ . Надежность обучения классификатора – это вероятность получения решающего правила с заданным качеством.

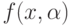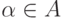Пусть $f(x,\alpha)$ – класс дискриминантных функций, где $\alpha\in A$ – параметр. Число степеней свободы при выборе конкретной функции в классе определяется количеством параметров в векторе $\alpha$ , т.е. размерностью .

Например, для классов линейных и квадратичных функций имеем:

Линейная дискриминантная функция: $f(x,\alpha)=\sum_{i=1}^n\alpha_i x_i+\alpha_0$ . В таком случае имеем n+1 степень свободы.

Квадратичная дискриминантная функция: 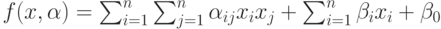$f(x,\alpha)=\sum_{i=1}^n\sum_{j=1}^n\alpha_{ij}x_i x_j+\sum_{i=1}^n\beta_i x_i+\beta_0$ . В таком случае имеем n^2+n+1 степеней свободы.

С увеличением степеней свободы увеличивается способность классификатора по разделению.

12.3. Вероятностная модель

Пусть прецеденты – это результат реализации случайных величин. Рассмотрим величину риска (т.е. ошибки) связанной с классификацией. Определим понятия риск среднего и риска эмпирического.

Пусть на $\Omega$ заданы $\sigma$ -алгебра и мера . Пусть также

– вектор признаков,
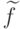$\widetilde{f}$ – класс функций, из которых выбирается решающее правило,
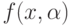$f(x,\alpha)$ – решающее правило (результат классификации), которое принимает значение 0 или 1 при фиксированном векторе параметра,
$\chi$ – характеристическая функция множества,
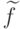– множество параметров, описывающие различные функции в $\widetilde{f}$ .

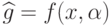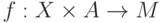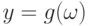Тогда $\widehat{g}=f(x,\alpha)$ , где $f\in\widetilde{f}$ и $f:X\times A\rightarrow M$ , $y=g(\omega)$ .

В данных обозначениях средний риск выглядит следующим образом:

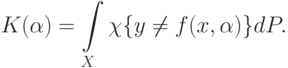
$K(\alpha)=\int\limits_X \chi\{y\neq f(x,\alpha)\}dP.$

Для случая двух классов, при 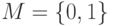$M=\{0,1\}$ , имеем:

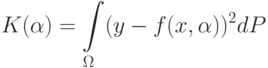
$K(\alpha)=\int\limits_{\Omega}(y-f(x,\alpha))^2 dP$

или

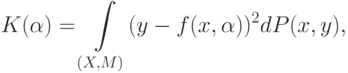
$K(\alpha)=\int\limits_{(X,M)}(y-f(x,\alpha))^2 dP(x,y),$

где

– это вероятностная мера на пространстве

.

12.4. Задача поиска наилучшего классификатора

Рассмотрим минимизацию функционала:

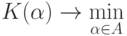
$K(\alpha)\rightarrow\min_{\alpha\in A}$

Задача же поиска наилучшего классификатора состоит в нахождении 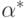$\alpha^*$ такого, что

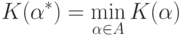
$K(\alpha^*)=\min_{\alpha\in A}K(\alpha)$

Если же минимума не существует, то надо найти 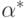$\alpha^*$ такое, что

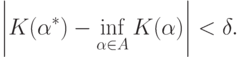
$\left| K(\alpha^*)-\inf_{\alpha\in A}K(\alpha) \right| <\delta.$

Другими словами, необходимо решить задачу минимизации среднего риска.

Поскольку неизвестно, будем решать задачу минимизации эмпирического риска. Пусть – число прецедентов. Тогда эмпирический риск задается выражением:

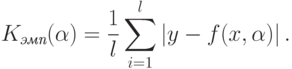
$K_{\textit{эмп}}(\alpha)=\frac{1}{l}\sum_{i=1}^l\left|y-f(x,\alpha)\right|.$

Таким образом, задача минимизации эмпирического риска выглядит так:

$K_{\textit{эмп}}(\alpha)\rightarrow\min_{\alpha\in A},$

где случайные величины мы минимизируем по параметру $\alpha$ – любой возможный параметр.

В идеале надо получить взаимосвязанные оценки эмпирического и среднего риска.

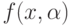Отметим, что чем меньше , тем легче построить $f(x,\alpha)$ такую, что $K_{\textit{эмп}}(\alpha)$ обращается в ноль, либо очень мало. Но при этом истинное значение $K(\alpha)$ может сильно отличаться от $K_{\textit{эмп}}(\alpha)$ . Необходимо выбрать $f(x,\alpha)$ такую, чтобы имела место равномерная сходимость по $\alpha$ выражения:

$P \left\{ \sup_{\alpha} \left| K_{\textit{эмп}}(\alpha)-K(\alpha) \right| >\varepsilon \right\} \xrightarrow[l\rightarrow\infty]{\phantom{0}} 0.$

Фактически это есть сходимость частот к математическому ожиданию.

В дальнейшем будем считать, что в зависимости от конкретного набора прецедентов можем получить любые $\alpha$ . Но необходимо, чтобы полученные эмпирическое решающее хорошо работало (отражало общие свойства) для всех образов. Поэтому в формуле присутствует равномерная сходимость.

Дальше >>

Математические методы распознавания образов

Математические методы распознавания образов