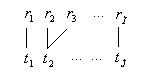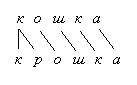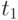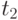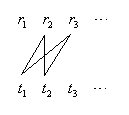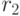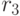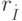| Азербайджан |
Классификация на основе сравнения с эталоном
Пусть задано множество образов (эталонов). Задача состоит в том, чтобы для тестируемого объекта выяснить, какой эталон ближе на основе меры сходства (расстояния между объектами). Данная задача и получила название "сравнение с эталонами".
В качестве эталонов могут рассматриваться следующие объекты:
- Буквы в словах рукописного текста (применительно к распознаванию рукописного текста);
- Силуэты объектов в сцене (применительно к машинному зрению);
- Слова (команды), произносимые человеком (применительно к распознаванию речи).
В этих примерах признаки не выделены, но можно измерить сходство. Например, сравнение слов: кошка ~ мошка ~ кора ~ норка и.т.д. Или силуэт объекта в сцене, чье положение и ориентация заранее не известны (применительно к машинному зрению, робототехнике).
8.1. Мера близости, основанная на поиске оптимального пути на графе
Рассмотрим строчный образ (слово). В данном случае можно выделить два критерия, на основе которых можно строить меру близости:
- совпадение букв,
- монотонность (совпадение порядка букв).
Пусть 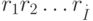 – эталон,
– эталон, 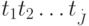 – пробный образ, причем
– пробный образ, причем  . Построим
соответствие между эталоном и пробным образом по следующему правилу:
каждому символу в первом слове должен соответствовать хотя бы один
символ во втором слове и каждому символу во втором слове должен
соответствовать хотя бы один символ в первом слове, (но соответствие
между символами не взаимнооднозначное, в частности, поскольку
. Построим
соответствие между эталоном и пробным образом по следующему правилу:
каждому символу в первом слове должен соответствовать хотя бы один
символ во втором слове и каждому символу во втором слове должен
соответствовать хотя бы один символ в первом слове, (но соответствие
между символами не взаимнооднозначное, в частности, поскольку  ).
).
Введем меру следующим образом:
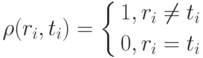
В качестве меры сходства двух слов принимаем соответствие, при котором суммарный вес всех дуг (изображенных на рисунках) минимален:
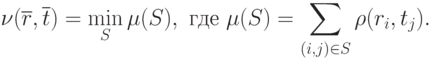
Через 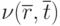 далее будем обозначать меру близости двух слов
далее будем обозначать меру близости двух слов 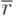 и
и 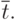
Соответствие  должно быть двудольным графом без изолированных
вершин с непересекающимися ребрами. Рассмотрим задачу сравнения
цепочек упорядоченных символов. В данной задаче могут возникать
следующие ошибки:
должно быть двудольным графом без изолированных
вершин с непересекающимися ребрами. Рассмотрим задачу сравнения
цепочек упорядоченных символов. В данной задаче могут возникать
следующие ошибки:
- неправильно определенный символ ( кошка – корка ),
- ошибка вставки ( кошка – кошрка ),
- ошибка потери ( кошка – кшка ).
Определение. Редакторским расстоянием называется минимальное
общее число изменений, вставок и потерь, требуемое для изменения
образа  в образ
в образ  :
:
![\def\I{\mathop{I}}
D(A,B)=\min_j\left[C(j)+\I\limits^{.}(j)+R(j)\right],](/sites/default/files/tex_cache/d02902bb684646a24f26781a604caae0.png)
 из
из  .
.Пусть
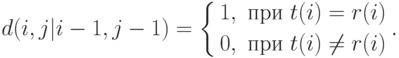
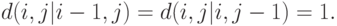
Построим таблицу, в которой столбцы – это символы образа, строки –
символы эталона. Количество точек в матрице есть  .
.
По данной таблице построим граф по следующему правилу. Если
отображается точка 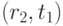 , то далее выбираем
, то далее выбираем 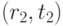 ,
, 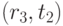 или
или 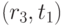 (т.е. возможны три
варианта). Соответствие слов реализуется в виде маршрута в графе. Этот
маршрут обязательно начинается с точки
(т.е. возможны три
варианта). Соответствие слов реализуется в виде маршрута в графе. Этот
маршрут обязательно начинается с точки 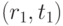 (иначе появится изолированная
точка) и заканчивается в
(иначе появится изолированная
точка) и заканчивается в 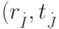 .
.
Таким образом, получили задачу выбора кратчайшего пути на графе от
точки 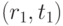 до точки
до точки 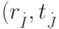 ,
где каждая вершина имеет свою стоимость: 0 или 1.
,
где каждая вершина имеет свою стоимость: 0 или 1.
8.2. Задача сравнения контуров
В качестве примера рассмотрим задачу сравнения контуров. Контура изображаются ломаными линиями, вершины которых будем называть узлами. Пусть заданы две линии – эталон и тестируемый объект. Используем следующую модель для сравнения объектов. Будем считать, что они изготовлены из проволоки и будем сравнивать близость этих ломаных путем оценки величины механической работы, которую нужно выполнить, чтобы преобразовать один объект в другой. Определим элементарную работу, которую надо совершить для перевода отдельных прямолинейных элементов ломаных. Достаточно рассмотреть два основных вида деформаций: растяжение (сжатие) и изгиб в узлах.
Каждой такой деформации припишем элементарную работу:
-
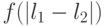 – работа по изменению длины при растяжении и сжатии,
– работа по изменению длины при растяжении и сжатии, -
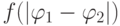 – работа по изменению угла при изгибе.
– работа по изменению угла при изгибе.
Задача состоит в поиске такого преобразования, чтобы затраченная работа была минимальной, т.е. надо найти
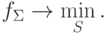
Эта задача сводится к установлению соответствия узлов одной ломаной
узлам другой. При этом не требуется взаимно-однозначное соответствие,
но требуется сохранение монотонности. Задача установления такого
соответствия, которое минимизирует общую работу по деформации ломаных,
также сводится к поиску минимального пути на графе такого же типа, как
и рассмотренный в предыдущем пункте. В графе каждая дуга получает вес 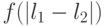 – работу по сжатию или растяжению, а для каждой вершины – вес
– работу по сжатию или растяжению, а для каждой вершины – вес 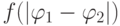 –
работу по изменению угла.
–
работу по изменению угла.