| Азербайджан |
Классификация на основе сравнения с эталоном
8.3. Задача сравнения речевых команд
В обработке речи можно выделить следующие основные направления:
- Распознавание отдельных слов (IWR – Isolated Word Recognition),
- Распознавание слитной речи (CSR – Continuous Speech Recognition).
- CDR – Speaker Dependent Recognition,
- SIR – Speaker Independent Recognition.
Ядром IWR-систем является совокупность эталонов и мера. Отрезок
сигнала (см. рис.) ![[0,T]](/sites/default/files/tex_cache/b74093923941d33ee19becc5f4b48b25.png) разбивается на сегменты, т.е. сигнал квантуется
(с перекрытием). С каждым сегментом связывается вектор коэффициентов
Фурье.
разбивается на сегменты, т.е. сигнал квантуется
(с перекрытием). С каждым сегментом связывается вектор коэффициентов
Фурье.
Обработка звука происходит в два этапа.
Первый этап. Строим цепочку 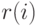 ,
, 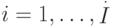 – разговорные сегменты. Далее
строим преобразование Фурье с разбиением на
– разговорные сегменты. Далее
строим преобразование Фурье с разбиением на 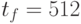 отрезков. Обозначим
через
отрезков. Обозначим
через 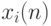 ,
, 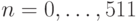 – отчеты для
– отчеты для  -ого сегмента,
-ого сегмента, 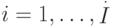 . Тогда
. Тогда
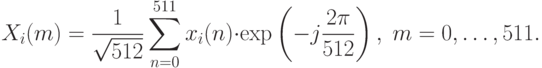
Рассмотрим первые 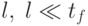 (пусть
(пусть 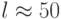 ),
коэффициентов Фурье в качестве вектора признаков:
),
коэффициентов Фурье в качестве вектора признаков:
![\def\I{\mathop{I}}
r(i)=
\left[
\begin{gathered}
X_i(0) \\
X_i(1) \\
\vdots \\
X_i(l-1)
\end{gathered}
\right],
\;l=1,\ldots,\I\limits^{.}](/sites/default/files/tex_cache/6eb3f4ff5737a5e583ada624365c326d.png)
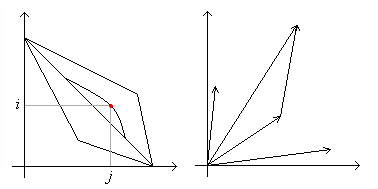
Второй этап. Определяем ограничения в графе соответствия сегментов эталонной и тестируемой команд.
Глобальные ограничения – ограничения поля для оптимального
маршрута, например, 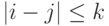 (рис. слева).
(рис. слева).
Локальные ограничения – монотонность на сети маршрутов (рис. справа).
Ограничения конечной точки.
Стоимость  – Евклидово расстояние между
– Евклидово расстояние между 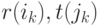 :
:
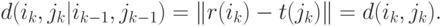
Таким образом, и эта задача также сводится к поиску кратчайшего пути на графе.
8.4. Динамическое программирование
Задача поиска кратчайшего пути на графе может быть решена
методом динамического программирования. Пусть 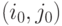 – начальный узел
(отправной город),
– начальный узел
(отправной город), 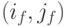 – конечный узел (город – пункт назначения). Тогда
задача состоит в поиске оптимального маршрута через промежуточные узлы
(города):
– конечный узел (город – пункт назначения). Тогда
задача состоит в поиске оптимального маршрута через промежуточные узлы
(города):

Пусть 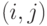 – промежуточный узел. Тогда по принципу оптимальности
Беллмана имеем
– промежуточный узел. Тогда по принципу оптимальности
Беллмана имеем
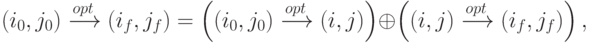
![D_{\min}(i_k,j_k)=\min_{(i_{k-1},j_{k-1})}
\left[
D_{\min}(i_{k-1},j_{k-1})+d(i_k,j_k|i_{k-1},j_{k-1})
\right]](/sites/default/files/tex_cache/318b1c6acb4f17c4c27b9e736217a585.png) .
.