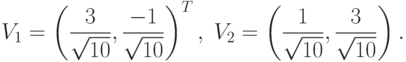| Азербайджан |
Классификация на основе байесовской теории решений
2.6. Классификаторы по минимуму расстояния
Будем рассматривать равновероятные классы с одинаковой матрицей ковариации.
Тогда  и выражение
и выражение
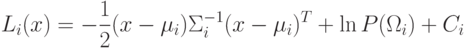
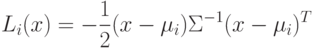
6.1. Классификатор по минимуму расстояния с диагональной
матрицей ковариации. Рассмотрим случай, когда матрица  диагональная с
одинаковыми элементами:
диагональная с
одинаковыми элементами: 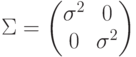 .
Тогда максимизация
.
Тогда максимизация 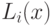 влечет минимизацию
евклидового расстояния, определяемое выражением
влечет минимизацию
евклидового расстояния, определяемое выражением 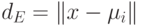 . В данном случае
будет считаться, что объект относится к данному классу, если он близок
в смысле евклидового расстояния.
. В данном случае
будет считаться, что объект относится к данному классу, если он близок
в смысле евклидового расстояния.
6.2. Классификатор по минимуму расстояния с недиагональной матрицей
ковариации. В этом случае максимизация 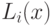 влечет минимизацию расстояния
Махалонобиса, определяемого выражением
влечет минимизацию расстояния
Махалонобиса, определяемого выражением 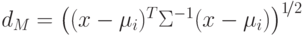 .
.
Т.к. матрица ковариации является симметрической, ее можно представить в виде:
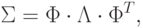
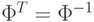 , а
, а  – диагональная
матрица с собственными значениями матрицы
– диагональная
матрица с собственными значениями матрицы  на диагонали. Матрица
на диагонали. Матрица  имеет столбцы, соответствующие собственным
векторам матрицы
имеет столбцы, соответствующие собственным
векторам матрицы  :
: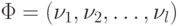
 :
:
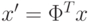 . Тогда координатами
. Тогда координатами 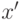 являются
являются 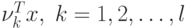 , т.е. проекции
, т.е. проекции  на собственные вектора. Другими словами, мы получили координаты в новой системе,
у которой оси определяются собственными векторами
на собственные вектора. Другими словами, мы получили координаты в новой системе,
у которой оси определяются собственными векторами 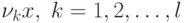 .
Тогда последнее уравнение преобразуется в уравнение эллипсоида в новой системе координат:
.
Тогда последнее уравнение преобразуется в уравнение эллипсоида в новой системе координат: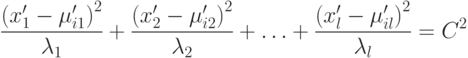
При 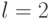 центр эллипса находится в точке
центр эллипса находится в точке 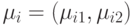 , а главные оси лежат по
собственным векторам и имеют длины
, а главные оси лежат по
собственным векторам и имеют длины  и
и  соответственно.
соответственно.
Пример. Рассмотрим двумерный двухклассовый случай
классификации двух нормально распределенных векторов с ковариационной
матрицей 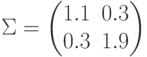 и средними значениями
и средними значениями  и
и 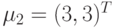 .
.
Найдем 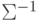 :
:
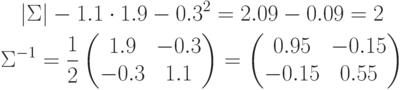
Классифицируем вектор 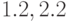 . Для этого посчитаем расстояние
Махалонобиса:
. Для этого посчитаем расстояние
Махалонобиса:
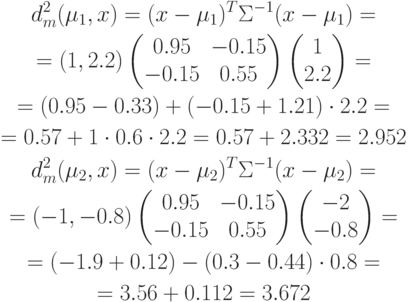
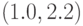 по евклидову расстоянию ближе
к точке
по евклидову расстоянию ближе
к точке 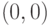 , чем к точке
, чем к точке 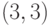 , но по расстоянию
Махалонобиса она ближе к
, но по расстоянию
Махалонобиса она ближе к 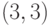 .
.Теперь вычислим главные оси эллипса с центром в точке 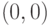 .
Для этого найдем собственные значения:
.
Для этого найдем собственные значения:
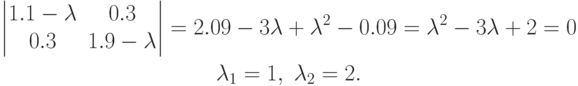
Тогда собственные вектора (и направление главных осей эллипса) будут иметь вид: