НОУ ИНТУИТ | Графы и алгоритмы. Лекция 12: Паросочетания

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Опубликован: 27.09.2006 | Уровень: специалист | Доступ: платный | ВУЗ: Нижегородский государственный университет им. Н.И.Лобачевского

|

Вам нравится? Нравится 42 студентам

| Поделиться |

Поддержать программу

Аннотация: Паросочетания и реберные покрытия. Метод увеличивающих путей. Паросочетания в двудольных графах. Паросочетания в произвольных графах (алгоритм Эдмондса).

Ключевые слова: Паросочетание, Реберным покрытием, вершина, определение, множества, аналогия, равенство, связь, число независимости, доказательство, значение, изолированная вершина, покрытие графа, компонента связности, граф, сильное, слабое, свободной,, путь, ребро, Чередующийся путь, увеличивающий, алгоритм, двудольный граф, четная, нечетная, расстояние, двудольный, дерево достижимости, дерево, поиск в ширину, множество вершин, очередь, Построение дерева достижимости, выход, ветвь, поиск, подграф, цветок, цикла, стягивание, операции

Паросочетания и реберные покрытия

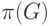Паросочетанием в графе называется множество ребер, попарно не имеющих общих вершин. Задача о паросочетании состоит в том, чтобы в данном графе найти паросочетание с наибольшим числом ребер. Это число для графа будем обозначать через $\pi(G)$ . Реберным покрытием графа называется такое множество ребер, что всякая вершина графа инцидентна хотя бы одному из этих ребер. Наименьшее число ребер в реберном покрытии графа обозначим через $\rho (G)$ . Заметим, что реберное покрытие существует только для графов без изолированных вершин.

Определение паросочетания похоже на определение независимого множества вершин, паросочетание иногда так и называют - независимое множество ребер. Эта аналогия еще усиливается тесной связью между реберными покрытиями и паросочетаниями, подобно тому, как связаны между собой вершинные покрытия и независимые множества. 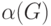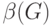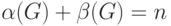Даже равенство, количественно выражающее эту связь, имеет точно такой же вид (напомним, что числа независимости $\alpha(G)$ и вершинного покрытия $\beta(G)$ связаны равенством $\alpha (G)+\beta (G)=n$ ). Приводимое ниже доказательство этого факта имеет алгоритмическое значение, так как показывает, каким образом каждая из двух задач может быть сведена к другой.

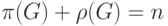Теорема 1. Для любого графа с вершинами, не имеющего изолированных вершин, справедливо равенство $\pi(G)+\rho (G)=n$ .

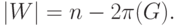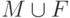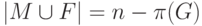Доказательство. Пусть - наибольшее паросочетание в графе . Обозначим через множество всех вершин графа, не покрытых ребрами этого паросочетания. Тогда $|W|=n-2\pi (G).$ Очевидно, что - независимое множество (иначе не было бы наибольшим). Выберем для каждой вершины из какое-нибудь инцидентное ей ребро. Пусть - множество всех выбранных ребер. 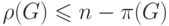Тогда $M\cup F$ - реберное покрытие и $|M\cup F|=n-\pi (G)$ , следовательно, $\rho (G)\le n-\pi (G)$ .

Обратно, пусть - наименьшее реберное покрытие графа . Рассмотрим подграф графа , образованный ребрами этого покрытия. В графе один из концов каждого ребра является вершиной степени 1 (ребро, каждая вершина которого инцидентна, по крайней мере, еще одному ребру, можно было бы удалить из , и оставшиеся ребра по-прежнему покрывали бы все вершины). Отсюда следует, что каждая компонента связности графа является звездой (звезда - это дерево, у которого не более одной вершины степени больше 1). Так как в любом лесе сумма количеств ребер и компонент связности равна числу вершин, то число компонент связности в графе равно $n-\rho(G)$ . Выбрав по одному ребру из каждой компоненты, получим паросочетание. 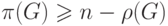Отсюда следует, что $\pi (G)\ge n-\rho (G)$ .

Несмотря на такое сходство между "вершинными" и "реберными" вариантами независимых множеств и покрытий, имеется кардинальное различие в сложности соответствующих экстремальных задач. "Вершинные" задачи, как уже отмечалось, являются NP-полными. Для реберных же известны полиномиальные алгоритмы. Они основаны на методе чередующихся путей, к рассмотрению которого мы теперь переходим. Отметим только еще, что ситуация похожа на ту, что наблюдается для задач об эйлеровом и гамильтоновом циклах - реберный вариант эффективно решается, а вершинный является NP-полным.

Дальше >>

Графы и алгоритмы

Графы и алгоритмы

Паросочетания

Паросочетания и реберные покрытия

Вопросы и ответы

Студенты

Авторизоваться

Графы и алгоритмы

Графы и алгоритмы

Паросочетания

Паросочетания и реберные покрытия

Вопросы и ответы

Студенты