|
Скажите, пожалуйста, можно ли еще получить документ о прохождении курса ("Графы и алгоритмы", декабрь 2020) после предоставления всех дополнительных необходимых документов? |
Инспектор
Вы можете этот курс.
Опубликован: 27.09.2006 | Уровень: специалист | Доступ: платный | ВУЗ: Нижегородский государственный университет им. Н.И.Лобачевского
Лекция 12:
Паросочетания
Алгоритм 1. Построение дерева достижимости
- объявить все вершины новыми
- объявить вершину
четной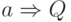 
- создать дерево
из одной вершины
-
while
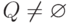do
-
if вершина
нечетная -
then if вершина не свободная
-
then
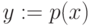
- объявить вершину
четной - добавить к дереву вершину
и ребро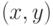
-
else for
do
-
if вершина новая
-
then
- объявить вершину нечетной
- добавить к вершину и ребро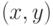
Если очередная рассматриваемая вершина оказывается
свободной (это выясняется при проверке в строке 8), нет необходимости
доводить построение дерева до конца. В этом случае путь между
вершинами и в дереве является увеличивающим
путем и его можно
использовать для построения большего паросочетания. После этого снова
выбирается свободная вершина (если такая еще есть) и строится дерево
достижимости. В приведенном тексте алгоритма соответствующий выход
отсутствует, но его легко предусмотреть, добавив ветвь else
к оператору if в строке 8.
Если дерево построено и в нем нет других свободных вершин, кроме корня, то нужно выбрать другую свободную вершину и построить дерево достижимости для нее (конечно, если в графе больше двух свободных вершин). При этом, как показывает следующая лемма, вершины первого дерева можно удалить из графа.
Лемма 2. Если дерево достижимости содержит хотя бы одну вершину увеличивающего пути, то оно содержит увеличивающий путь.
Доказательство. Пусть дерево достижимости
с корнем
имеет общие вершины с увеличивающим путем 
, соединяющим
свободные вершины 
и 
. Покажем, что
в
есть увеличивающий путь (это не обязательно путь ). Достаточно
доказать, что хотя бы одна из вершин , принадлежит
дереву . Если одна из них совпадает с вершиной ,
то из
теоремы 1 следует, что и другая принадлежит дереву, так что в этом случае
в дереве имеется увеличивающий путь между вершинами
и .
Допустим, обе вершины и отличны
от .
Пусть 
- простой путь, начинающийся в вершине , заканчивающийся
в вершине , принадлежащей пути , и не содержащий
других
вершин пути . Очевидно, что последнее ребро пути
слабое. Вершина делит путь на два отрезка
- 
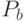и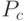 
, - содержащие соответственно вершины
и .
В одном из этих отрезков, скажем, в 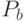, ребро, инцидентное
вершине , - сильное. Тогда объединение путей и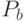
образует чередующийся путь, соединяющий вершины
и .
По теореме 1, вершина принадлежит дереву .
Из этой леммы следует, что если полностью построенное дерево достижимости не содержит других свободных вершин, кроме корня, то ни одна вершина этого дерева не принадлежит никакому увеличивающему пути. Поэтому, приступая к построению следующего дерева достижимости, вершины первого дерева можно удалить из графа (временно, конечно). Этот процесс - построение деревьев достижимости и удаление их вершин из графа - продолжается до тех пор, пока либо будет найден увеличивающий путь, либо останется граф с не более чем одной свободной вершиной. В первом случае паросочетание увеличивается, граф восстанавливается, и вновь начинается поиск увеличивающего пути. Во втором случае имеющееся паросочетание является наибольшим.
Так как при поиске в ширину каждое ребро исследуется не более чем дважды,
то общее время поиска увеличивающего пути для данного паросочетания
есть 
. Число ребер в паросочетании не может
превышать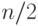 
, поэтому
общая сложность алгоритма будет 
.
Татьяна Наумович
