|
Скажите, пожалуйста, можно ли еще получить документ о прохождении курса ("Графы и алгоритмы", декабрь 2020) после предоставления всех дополнительных необходимых документов? |
Паросочетания
Выявление цветков не представляет трудности - нужно только добавить
ветвь else к оператору if в строке 14 алгоритма 1. Первое, что
мы сделаем, обнаружив цветок, - превратим все сильные ребра
пути  в слабые, а слабые - в сильные. После этого преобразования множество
сильных ребер является паросочетанием той же мощности, но вместо
вершины
в слабые, а слабые - в сильные. После этого преобразования множество
сильных ребер является паросочетанием той же мощности, но вместо
вершины  свободной вершиной станет вершина
свободной вершиной станет вершина  . Таким образом, на
цикле
. Таким образом, на
цикле  будет одна свободная вершина и этот цикл
является чередующимся путем, который начинается и заканчивается в этой
вершине. Покажем, что такой цикл можно стянуть в одну вершину, не теряя
информации о существовании увеличивающих путей.
будет одна свободная вершина и этот цикл
является чередующимся путем, который начинается и заканчивается в этой
вершине. Покажем, что такой цикл можно стянуть в одну вершину, не теряя
информации о существовании увеличивающих путей.
Операция стягивания подграфа  в графе
в графе  состоит
в следующем. Все вершины этого подграфа удаляются из графа, а вместо них
добавляется новая вершина. Эта новая вершина соединяется ребрами с теми
и только теми из оставшихся вершин графа, которые были смежны хотя бы
с одной вершиной подграфа
состоит
в следующем. Все вершины этого подграфа удаляются из графа, а вместо них
добавляется новая вершина. Эта новая вершина соединяется ребрами с теми
и только теми из оставшихся вершин графа, которые были смежны хотя бы
с одной вершиной подграфа  . Граф, получаемый в результате такой
операции, будем обозначать через
. Граф, получаемый в результате такой
операции, будем обозначать через 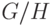 .
.
Теорема 3. Пусть  - паросочетание в графе
- паросочетание в графе  ,
,  - цикл длины
- цикл длины 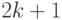 в этом графе, причем на
цикле имеется
в этом графе, причем на
цикле имеется  сильных ребер и одна свободная вершина.
Пусть
сильных ребер и одна свободная вершина.
Пусть 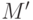 - паросочетание в графе
- паросочетание в графе  ,
составленное
из всех ребер паросочетания
,
составленное
из всех ребер паросочетания  , не принадлежащих
циклу
, не принадлежащих
циклу  . Паросочетание
. Паросочетание  является наибольшим
в графе
является наибольшим
в графе  тогда и только тогда, когда
тогда и только тогда, когда 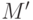 -
наибольшее паросочетание в графе
-
наибольшее паросочетание в графе 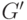 .
.
Доказательство. Докажем, что из существования увеличивающего пути относительно
паросочетания  в графе
в графе  следует, что существует
увеличивающий путь относительно паросочетания
следует, что существует
увеличивающий путь относительно паросочетания 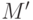 в графе
в графе 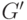 и обратно.
и обратно.
Пусть  - свободная вершина цикла
- свободная вершина цикла  . Новую
вершину,
образованную в графе
. Новую
вершину,
образованную в графе 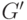 при стягивании цикла
при стягивании цикла  ,
обозначим через
,
обозначим через  . Отметим, что она является свободной вершиной
относительно паросочетания
. Отметим, что она является свободной вершиной
относительно паросочетания 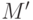 .
.
Пусть  - увеличивающий путь в графе
- увеличивающий путь в графе  .
Если он не
содержит вершин цикла
.
Если он не
содержит вершин цикла  , то он будет увеличивающим путем и в графе
, то он будет увеличивающим путем и в графе 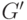 . В противном случае рассмотрим отрезок
. В противном случае рассмотрим отрезок 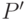 пути
пути  ,
начинающийся в свободной вершине, отличной от
,
начинающийся в свободной вершине, отличной от  , заканчивающийся
в вершине
, заканчивающийся
в вершине  , лежащей на цикле
, лежащей на цикле  , и не содержащий
других
вершин цикла
, и не содержащий
других
вершин цикла  . Если в пути
. Если в пути 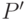 заменить вершину
заменить вершину  вершиной
вершиной  , то, очевидно, получится увеличивающий путь
в графе
, то, очевидно, получится увеличивающий путь
в графе 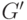 .
.
Обратно, пусть 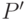 - увеличивающий путь в
графе
- увеличивающий путь в
графе 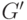 .
Если
.
Если 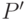 не проходит через вершину
не проходит через вершину  , то он будет
увеличивающим путем
и в графе
, то он будет
увеличивающим путем
и в графе  . В противном случае рассмотрим путь
. В противном случае рассмотрим путь 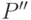 ,
получающийся удалением вершины
,
получающийся удалением вершины  из пути
из пути 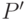 .
Можно считать,
что вершина
.
Можно считать,
что вершина  была последней вершиной пути
была последней вершиной пути 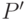 , а
путь
, а
путь 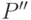 заканчивается в предпоследней вершине
заканчивается в предпоследней вершине  . Так как
вершина
. Так как
вершина  смежна с вершиной
смежна с вершиной  в графе
в графе 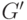 , то в
графе
, то в
графе  на цикле
на цикле  имеется вершина
имеется вершина  , смежная
с
, смежная
с  . Добавим
к пути
. Добавим
к пути 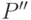 тот из отрезков цикла
тот из отрезков цикла  , соединяющих
вершину
, соединяющих
вершину  с вершиной
с вершиной  , который начинается сильным ребром.
В результате получится увеличивающий путь в графе
, который начинается сильным ребром.
В результате получится увеличивающий путь в графе  .
.
Из доказательства видно, что увеличивающий путь в графе  при
известном увеличивающем пути в графе
при
известном увеличивающем пути в графе 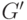 находится за линейное
время. Для получения оценок времени работы алгоритма в целом требуется еще
проработка ряда деталей, например подробностей выполнения операции
стягивания и т.д. Однако ясно, что это время ограничено полиномом.
находится за линейное
время. Для получения оценок времени работы алгоритма в целом требуется еще
проработка ряда деталей, например подробностей выполнения операции
стягивания и т.д. Однако ясно, что это время ограничено полиномом.
