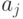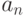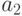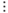|
как начать заново проходить курс, если уже пройдено несколько лекций со сданными тестами? |
Алгебраические системы
3.1 Алгебраические системы
Мы предполагаем, что читатель владеет понятиями группа, кольцо, поле. Поэтому очень кратко изложим элементы теории с нужными нам для дальнейшего акцентами.
3.1.1 Алгебраическая операция
В основе всех понятий, изучаемых в различных разделах алгебры, лежит понятие алгебраической операции.
Пусть  - множество (элементами
- множество (элементами  могут быть числа или функции или объекты геометрической природы и т.д.).
могут быть числа или функции или объекты геометрической природы и т.д.).
Определение 3.1 Говорят, что на  задана бинарная алгебраическая операция, если любой упорядоченной паре
задана бинарная алгебраическая операция, если любой упорядоченной паре 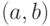 элементов
элементов  ставится в соответствие однозначно определённый элемент
ставится в соответствие однозначно определённый элемент 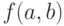 этого же множества
этого же множества  .
.
Определение 3.2 Группоидом называется всякое непустое множество, в котором задана алгебраическая операция.
Иногда вместо 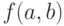 пишут
пишут  , а ещё чаще бинарную операцию на
, а ещё чаще бинарную операцию на  обозначают каким-нибудь специальным символом:
обозначают каким-нибудь специальным символом:  ,
,  ,
,  ,
, 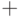 , так будем поступать и мы, называя
, так будем поступать и мы, называя 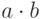 (или просто
(или просто  ) произведением элементов
) произведением элементов  и
и  . Таким образом, равенство
. Таким образом, равенство
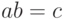 |
( 3.1) |
будет в дальнейшем иметь следующий смысл: упорядоченной паре 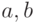 из
из  ставится в соответствие элемент
ставится в соответствие элемент  . Иногда (там, где это будет удобнее) вместо "произведение" будем заменять на "сумму", см. таблицу 3.1.
. Иногда (там, где это будет удобнее) вместо "произведение" будем заменять на "сумму", см. таблицу 3.1.
Замечание 1. Можно рассматривать бинарную операцию в "широком смысле": некоторым упорядоченным парам элементов из  ставится в соответствие один или несколько элементов из
ставится в соответствие один или несколько элементов из  . Такой, более общий подход "имеет право на существование", он приводит к интересным результатам, однако мы, исходя из наших целей, будем придерживаться понятия алгебраической операции, приведённого выше.
. Такой, более общий подход "имеет право на существование", он приводит к интересным результатам, однако мы, исходя из наших целей, будем придерживаться понятия алгебраической операции, приведённого выше.
Замечание 2. Наряду с бинарными алгебраическими операциями имеет смысл рассматривать и более общие  -арные операции (унарные при
-арные операции (унарные при 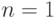 , тернарные при
, тернарные при 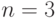 , и т.д.), а также и их комбинации. Нас же будут интересовать, за редкими исключениями, именно бинарные операции.
, и т.д.), а также и их комбинации. Нас же будут интересовать, за редкими исключениями, именно бинарные операции.
На множестве  можно задать много различных операций. Если хотят выделить одну из них, то пишут
можно задать много различных операций. Если хотят выделить одну из них, то пишут  .
.
Пример 3.1
- На множестве целых чисел определены операции сложения и умножения. Таким образом, заданы группоиды
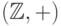 и
и 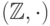 .
. - На
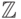 можно задать и другие операции:
можно задать и другие операции: 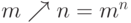 ,
, 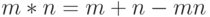 , получим группоиды
, получим группоиды 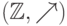 и
и 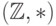 , и т.д.
, и т.д. - На множестве
 невырожденных матриц порядка
невырожденных матриц порядка  (
( ): а) матричное умножение - алгебраическая операция, б) матричное сложение - нет.
): а) матричное умножение - алгебраическая операция, б) матричное сложение - нет. - Пусть
 . Сложение не является бинарной алгебраической операцией (объясните, почему).
. Сложение не является бинарной алгебраической операцией (объясните, почему). - Рассмотрим множество векторов на плоскости. Скалярное произведение векторов не является алгебраической операцией (почему?).
- Рассмотрим множество векторов на плоскости и определим сложение векторов по "правилу треугольника". Это - алгебраическая операция.
- Векторное произведение векторов - алгебраическая операция.
Для задания группоида нужно задать множество  и то правило, по которому можно найти значение операции
и то правило, по которому можно найти значение операции  для любых двух элементов из
для любых двух элементов из  . В том случае, когда множество
. В том случае, когда множество  конечно, всю эту информацию можно записать таблицей, в которой входной строкой и входным столбцом является список элементов множества
конечно, всю эту информацию можно записать таблицей, в которой входной строкой и входным столбцом является список элементов множества  , а на пересечении строки с входом
, а на пересечении строки с входом  и столбца с входом
и столбца с входом  располагается значение операции
располагается значение операции  .
.
Такая таблица называется таблицей Кэли для группоида 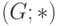 в честь английского математика Артура Кэли (1821-1895). Если
в честь английского математика Артура Кэли (1821-1895). Если 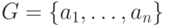 , то таблица Кэли для группоида
, то таблица Кэли для группоида  имеет следующий вид:
имеет следующий вид:
Исходя из такого задания группоида, легко подсчитать, сколько различных операций можно определить на множестве  порядка
порядка  . В каждую из
. В каждую из 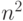 клеток таблицы Кэли можно записать любой из
клеток таблицы Кэли можно записать любой из  элементов множества
элементов множества  . Отсюда видно, что таблицу Кэли можно составить в
. Отсюда видно, что таблицу Кэли можно составить в 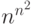 вариантах, то есть на множестве
вариантах, то есть на множестве  из
из  элементов существуют
элементов существуют 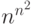 различных группоидов.
различных группоидов.
| Мультипликативная терминология | Аддитивная терминология |
|---|---|
Умножение 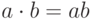
|
Сложение 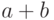
|
 , ,  - множители - множители |
 , ,  - слагаемые - слагаемые |
Нейтральный элемент - единица ( ) ) |
Нейтральный элемент - ноль ( ) ) |
Обратный элемент 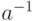
|
Противоположный элемент 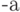
|
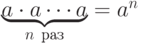 - степень - степень |
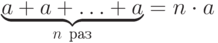 - кратное - кратное |
3.1.2 Нейтральные и обратные элементы
Определение 3.3 Элемент 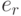 (или
(или 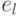 ) группоида
) группоида 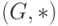 называется правым (соответственно, левым) нейтральным, если
называется правым (соответственно, левым) нейтральным, если  для любого элемента
для любого элемента 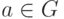 (соответственно,
(соответственно, 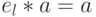 ). Элемент
). Элемент  группоида
группоида 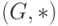 называется нейтральным, если он является одновременно левым и правым нейтральным.
называется нейтральным, если он является одновременно левым и правым нейтральным.
Ясно, что если в группоиде существует нейтральный элемент, то он единственный.
В зависимости от терминологии (см. таблицу 3.1), нейтральный элемент могут называть единицей или нулем.
Определение 3.4 Пусть  - группоид,
- группоид,  - его правый (или левый) нейтральный элемент, и
- его правый (или левый) нейтральный элемент, и 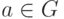 , то правым (соответственно, левым) обратным элементом для элемента
, то правым (соответственно, левым) обратным элементом для элемента  относительно правого (или левого) нейтрального элемента
относительно правого (или левого) нейтрального элемента  называется такой
называется такой 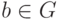 , что
, что 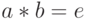 (соответствено,
(соответствено, 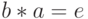 ).
).
В общем случае в группоиде с нейтральным элементом элемент может не иметь обратных, может иметь один или несколько обратных. Более определённо вопрос о числе обратных элементов решается в группоидах с ассоциативной операцией, см. ниже.
Конструировать разные бинарные операции на множестве можно неограниченно, но задача изучения произвольных алгебраических структур слишком обща. Поэтому рассматривают структуры при некоторых естественных ограничениях.
Чаще всего нас будет интересовать выполнимость ассоциативного и коммутативного законов для операции.