|
как начать заново проходить курс, если уже пройдено несколько лекций со сданными тестами? |
Основы теории чисел
1.1 Основы теории чисел
При необходимости более глубокого знакомства с материалом можно воспользоваться любым из университетских учебников алгебры и теории чисел. Кроме того, имеются пособия по криптографии, содержащие необходимый минимум теоретических сведений в указанных областях. В частности, отметим пособие [1], особенно полезными мы считаем главы 2 и 3 этой книги. Мы приводим краткие сведения из теории и примеры решения некоторых задач по теории чисел.
1.1.1 Делимость
Будем считать известными свойства операций над целыми числами (сложения, вычитания, умножения), понятие модуля целого числа и свойства модуля.
Рассмотрим свойства отношения делимости во множестве целых чисел, это множество обозначается 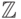 .
.
Определение 1.1 Целое число  делится на целое число
делится на целое число  , если существует такое целое число
, если существует такое целое число  , что
, что 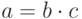 . Число
. Число  называется делимым,
называется делимым,  - делителем,
- делителем,  - частным.
- частным.
Если число  делится на
делится на  , то пишут
, то пишут 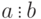 (
( кратно
кратно  ).
).
Отношение делимости 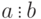 в
в 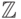 обладает следующими свойствами:
обладает следующими свойствами:
- Для любого
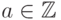 имеем
имеем 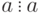 .
. -
Отношение делимости транзитивно, т. е. из
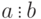 и
и 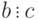 следует
следует  .
. - Если
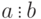 , то
, то 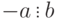 ,
, 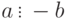 и
и 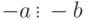 , т. е. отношение делимости сохраняется при изменении знаков делимого и делителя.
, т. е. отношение делимости сохраняется при изменении знаков делимого и делителя.
- Если
 и
и 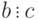 , то
, то 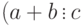 .
. -
Если
Отметим, что утверждения, обратные 4 и 5, ложны: из делимости суммы не вытекает делимость слагаемых, а из делимости произведения не вытекает делимость сомножителей. и
и 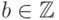 , то
, то 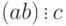 .
.Например,
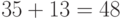 делится на 12, но ни 35, ни 13 не делятся на 12;
делится на 12, но ни 35, ни 13 не делятся на 12; 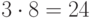 делится на 12, но ни 3, ни 8 на 12 не делятся.
делится на 12, но ни 3, ни 8 на 12 не делятся. - Если
 , а
, а  не делится на
не делится на  , то
, то  не делится на
не делится на  .
. - Нуль делится на любое число
 .
. - Любое число
 делится на 1.
делится на 1. - Если
 , то не существует такого
, то не существует такого  , что
, что 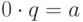 .
. - Если
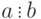 , то
, то  .
.
1.1.2 Деление с остатком
Определение 1.2 Разделить целое число  на целое число
на целое число  с остатком - это значит найти два таких целых числа
с остатком - это значит найти два таких целых числа  и
и  , чтобы выполнялись условия:
, чтобы выполнялись условия:

-
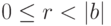 .
.
Число  называется неполным частным, а число
называется неполным частным, а число  - остатком от деления
- остатком от деления  на
на  .
.
Заметим, что остаток - всегда есть число неотрицательное, а вот неполное частное может быть каким угодно целым числом. Поэтому на вопрос: "Сколько будет минус пять поделить на три с остатком?", правильный ответ: "Неполное частное минус два, остаток - один".
Теорема 1.1 Каковы бы ни были целое число a и целое число  , всегда возможно, и притом единственным способом, разделить
, всегда возможно, и притом единственным способом, разделить  на
на  с остатком.
с остатком.
1.1.3 Наибольший общий делитель
Определение 1.3 Целое число 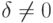 называется общим делителем целых чисел
называется общим делителем целых чисел 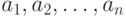 , если каждое из этих чисел делится на
, если каждое из этих чисел делится на  .
.
Определение 1.4 Целое число  называется наибольшим общим делителем чисел
называется наибольшим общим делителем чисел 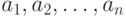 , если:
, если:
 является общим делителем этих чисел;
является общим делителем этих чисел; делится на любой общий делитель чисел
делится на любой общий делитель чисел 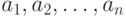 .
.
Теорема 1.2 Наибольший общий делитель чисел 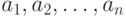 определён однозначно с точностью до знака (т.е. если
определён однозначно с точностью до знака (т.е. если 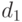 и
и  наибольшие общие делители чисел
наибольшие общие делители чисел 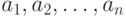 , то либо
, то либо  , либо
, либо 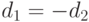 ).
).
Условимся всегда рассматривать положительное значение наибольшего общего делителя чисел 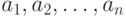 . Обозначение:
. Обозначение: 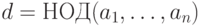 .
.
Пример 1.1 
Действительно, множество положительных делителей числа 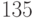 есть
есть 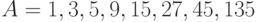 , а для числа
, а для числа 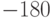 такое множество имеет вид
такое множество имеет вид 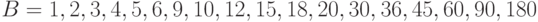 . Пересечение этих множеств
. Пересечение этих множеств 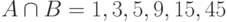 . Число
. Число  является общим делителем чисел
является общим делителем чисел 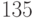 и
и 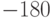 и делится на все остальные общие делители этих чисел. Значит,
и делится на все остальные общие делители этих чисел. Значит,  . Заметим, что
. Заметим, что  - наибольший по величине положительный общий делитель чисел
- наибольший по величине положительный общий делитель чисел 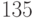 и
и 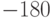 .
.
Для любых целых чисел 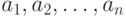 их наибольший общий делитель является наибольшим по величине положительным общим делителем.
их наибольший общий делитель является наибольшим по величине положительным общим делителем.
Однако данное здесь определение является более удобным, так как распространяется на достаточно большой класс объектов, в частности, на многочлены. Определение же, включающее слова "наибольший по величине", не применимо к многочленам.

