НОУ ИНТУИТ | Криптографические методы защиты информации. Лекция 1: Основы теории чисел

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

|

Вам нравится? Нравится 57 студентам

| Поделиться |

Поддержать программу

1.4 Сравнения первой степени и неопределенные уравнения

Одно уравнение с несколькими неизвестными имеет, как правило, бесконечное множество решений. Поэтому такие уравнения называют неопределенными. В теории чисел рассматривают задачу отыскания целочисленных решений неопределенных уравнений (их еще называют диофантовыми по имени древнегреческого математика Диофанта). Связь сравнений и диофантовых уравнений дается следующей теоремой.

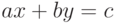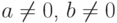Теорема 1.22 Если $({x}_{0}, {y}_{0})$ - целочисленное решение неопределенного уравнения , где , , - целые числа, $a \neq 0$, $b \neq 0$ , то - решение сравнения $ax_0=c ~(mod \ b)$ .

Обратно, если - решение сравнения $ax=c ~(mod \ b)$ , то существует такое целое число , что - решение неопределенного уравнения .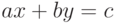

Эта теорема позволяет свести решение неопределенных уравнений вида $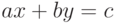 ax+by=c к решению сравнений первой степени, и обратно. В частности, из приведенных выше утверждений о сравнениях первой степени легко получается

Теорема 1.23 Если 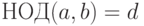, то неопределенное уравнение 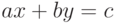имеет целочисленное решение в том и только в том случае, когда делится на .

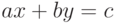В частности, если НОД(a,b)=1 , то урвнение ax+by=c при любом целом c имеет целочисленное решение.

Процесс нахождения целочисленных решений уравнений вида 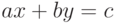ax+by=c состоит из даух этапов: нахождение хотя бы одного такого решения и нахождение общего вида таких решений. Рассмотрим сначала второй этап.

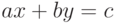Теорема 1.24 Если известно частное целочисленное решение $({x}_{0}, {y}_{0})$ неопределенного уравнения и 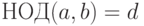, то общее решение этого уравнения имеет вид 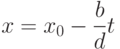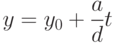$x= {x}_{0}-\dfrac{b}{d}t$ , $y= {y}_{0}+\dfrac{a}{d}t$ , где пробегает множество целых чисел.

Для нахождения частных решений применяют те же способы, что и для решения сравнений (например, можно использовать теорему Эйлера). Покажем, как искать решения неопределенных уравнений (а тем самым и сравнений) с помощью цепных дробей.

Из предыдущего следует, что общее решение уравнения имеет вид:

$x= {(-1)}^{n-1} c {Q}_{n-1}-bt, y= {(-1)}^{n} c {P}_{n-1}+at,$

где ${P}_{n-1}$ и ${Q}_{n-1}$ - числитель и знаменатель предпоследней подходящей дроби разложения $\frac{a}{b}$ в цепную дробь, а - любое целое число.

Пример 1.33 Решим в целых числах уравнение .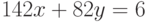

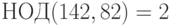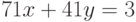Решение. Так как НОД(142,82)=2 и $6\, \vdots \,2$ , то уравнение имеет решение. Данное уравнение равносильно уравнению 71x+41y=3 .

Разложим $\dfrac{71}{41}$ в цепную дробь : $\dfrac{71}{41}=[1; 1,2,1,2,1,2]$ .

Составим все подходящие дроби:

$\frac{{P}_{0}}{{Q}_{0}}= \frac{1}{1},~~ \frac{{P}_{1}}{{Q}_{1}}=\frac{2}{1},~~\frac{{P}_{2}}{{Q}_{2}}= \frac{5}{3},~~ \frac{{P}_{3}}{{Q}_{3}}=\frac{7}{4},~~\frac{{P}_{4}}{{Q}_{4}}=\frac{19}{11},~~ \frac{{P}_{5}}{{Q}_{5}}=\frac{26}{15},~~\frac{{P}_{6}}{{Q}_{6}}=\frac{71}{41}.$

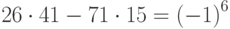На основании свойства подходящих дробей ${P}_{k-1}{Q}_{k}- {P}_{k}{Q}_{k-1}= {(-1)}^{k}$ Получим: $26\cdot41-71\cdot15= {(-1)}^{6}$ , или $71\cdot(-15)+41\cdot26=1$ .

Умножив обе части равенства на 3, находим: 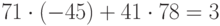$71\cdot(-45)+41\cdot78=3$ , т.е. 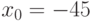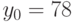${x}_{0}=-45$ , ${y}_{0}=78$ - частное решение данного уравнения.

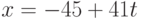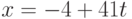Все решения могут быть найдены по формулам: x=-45+41t , y=78-71t , или x=-4+41t , y=7-71t , где принимает любые целые значения.

1.5 Китайская теорема об остатках

Рассмотрим систему сравнений первой степени:

$x\equiv {a}_{1} (mod \ {m}_{1}), x\equiv {a}_{2} (mod \ {m}_{2}), {\dots}, x\equiv {a}_{r} (mod \ {m}_{r}),$

( 1.9)

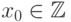где числа ${m}_{1},{m}_{2},...,{m}_{r}$ попарно взаимно простые, и найдём значение ${x}_{0} \in \mathbb{Z}$ , удовлетворяющее всем сравнениям.

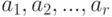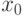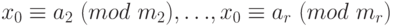Теорема 1.25 (китайская теорема об остатках) Пусть ${m}_{1},{m}_{2},...,{m}_{r}$ - попарно взаимно простые, и числа ${a}_{1},{a}_{2},...,{a}_{r}$ - произвольные целые. Тогда существует единственное такое целое число ${x}_{0}$ , что $0 \leq x_{0} < {m}_{1} \cdot {m}_{2} \cdot \dots \cdot {m}_{r}$ и ${x}_{0}\equiv{a}_{1}~(mod \ {m}_{1})$ , ${x}_{0}\equiv {a}_{2}~(mod \ {m}_{2}), {\dots}, {x}_{0}\equiv {a}_{r}~(mod \ {m}_{r})$ .

${x}_{0}\equiv \sum _{i=1}^{r}{{a}_{1}}{M}_{i}{N}_{i}~(mod \ m_1) \cdot {m}_{2} \cdot ... \cdot {m}_{r},$

( 1.10)

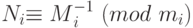где ${M}_{i}={m}_{1} \cdot {\dots}{ \cdot m}_{i-1} \cdot {m}_{i+1} \cdot {\dots}{ \cdot m}_{r}$ и ${N}_{i}{ \equiv M}_{i}^{-1}~(mod \ m_i)$ .

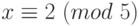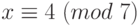Пример 1.34 Решим систему сравнений $x\equiv 2 ~(mod \ 5)$ , $x\equiv 3 ~(mod \ 6)$ , $x\equiv 4 ~(mod \ 7)$ .

Вычисляем: 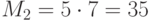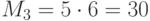${M}_{1}=6 \cdot 7=42$ , ${M}_{2}=5 \cdot 7=35$ , ${M}_{3}=5 \cdot 6=30$ . Находим обратные числа:

${N}_{1} \equiv {42}^{-1} \equiv {2}^{-1} \equiv 3mod5;$

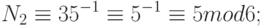
${N}_{2} \equiv {35}^{-1} \equiv {5}^{-1} \equiv 5mod6;$

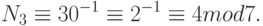
${N}_{3} \equiv {30}^{-1} \equiv {2}^{-1} \equiv 4mod7.$

Подставляем значения в формулу (1.10):

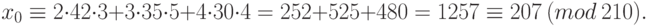
${x}_{0}\equiv 2 \cdot 42 \cdot 3+3 \cdot 35 \cdot 5+4 \cdot 30 \cdot 4=252+525+480=1257\equiv 207 ~(mod \ 210).$

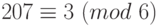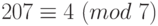Проверка: $207-2=205=5 \cdot 41$ , то есть $207\equiv 2 ~(mod \ 5)$ ; $207-3=204=6 \cdot 34$ , то есть $207\equiv 3 ~(mod \ 6)$ ; $207-4=203=7 \cdot 29$ , то есть $207\equiv 4 ~(mod \ 7)$ .

1.5.1 Следствие Китайской теоремы об остатках

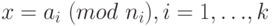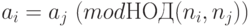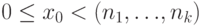Теорема 1.26 Система сравнений $x={a}_{i} ~(mod \ n_i),i=1,{\dots},k$ , имеет решение тогда и только тогда, когда ${a}_{i}={a}_{j}~(mod НОД(n_i,n_j))$ , причем такое с условием $0\leq x_0<\LCM({n}_{1},{\dots},{n}_{k})$ - единственное.

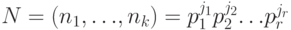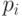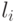Для решения системы найдём $N=\LCM\left({n}_{1},{\dots},{n}_{k}\right)={p}_{1}^{{j}_{1}}{p}_{2}^{{j}_{2}}{\dots}{p}_{r}^{{j}_{r}}$ , где ${p}_{i}$ - попарно различные простые числа. Для каждого делителя ${p}_{i}^{{j}_{i}}$ найдём номер ${l}_{i}$ такой, что 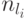${n}_{{l}_{i}}$ делится на него, и число 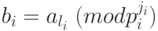${b}_{i}={a}_{{l}_{i}}~(mod p_{i}^{{j}_{i}})$ . 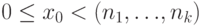Полученная система $x={b}_{i}~(mod p_{i}^{{j}_{i}})$ будет иметь взаимно простые модули, и единственное её решение x_0 с условием $0\leq x_0<\LCM({n}_{1},{\dots},{n}_{k})$ даёт Китайская теорема об остатках.

Пример 1.35 Решим систему уравнений: x=12mod14 , x=4mod18 , x=4mod12 .

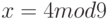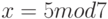Решение. Нетрудно убедиться, что наша система удовлетворяет условию теоремы. Решим её. Найдём $\LCM\left(14,18,12\right)=4 \cdot 9 \cdot 7=252.$ На 4, 7 и 9 делятся, соответственно, 12, 14 и 18. Следовательно, исходная система эквивалентна системе: x=0mod4 , x=4mod9 и x=5mod7 . Решение x=40mod252 последней системы находим по китайской теореме об остатках.