|
как начать заново проходить курс, если уже пройдено несколько лекций со сданными тестами? |
Хэш-функции и электронная подпись
9.1 Хэш-функции
Определение 9.1 Хэш-функции - это функции, предназначенные для "сжатия" произвольного сообщения, записанного, как правило, в двоичном алфавите, в некоторую битовую последовательность фиксированной длины, называемую сверткой.
Хэш-функции применяются для тестирования логических устройств, для быстрого поиска и проверки целостности записей в базах данных.
В криптографии хэш-функции применяются для решения следующих задач:
- построения систем контроля целостности данных при их передаче или хранении,
- аутентификация источника данных.
При решении первой задачи для каждого набора данных вычисляется значение хеш-функции (называемое кодом аутентификации сообщения или имитовставкой), которое передается или хранится вместе с самими данными. При получении данных пользователь вычисляет значение свертки и сравнивает его с имеющимся контрольным значением. Несовпадение говорит о том, что данные были изменены. При решении второй задачи, аутентификации источника данных, мы имеем дело с не доверяющими друг другу сторонами. В связи с этим подход, при котором обе стороны обладают одним и тем же секретным ключом, уже не применим. В такой ситуации применяют схемы цифровой подписи, позволяющие осуществить аутентификацию источника данных. Как правило, при этом сообщение, прежде чем быть подписано личной подписью, основанной на секретном ключе пользователя, "сжимается" с помощью хеш-функции, выполняющей функцию кода обнаружения ошибок.
Определение 9.2 Обозначим через  множество, элементы которого будем называть сообщениями,
множество, элементы которого будем называть сообщениями,  - натуральное число. Хеш-функцией называется всякая легко вычислимая функция
- натуральное число. Хеш-функцией называется всякая легко вычислимая функция 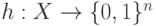 .
.
Кроме того, хэш-функцию можно понимать, как отображение из множества сообщений в некоторое ограниченное подмножество целых неотрицательных чисел.
Обычно число возможных сообщений значительно превосходит число возможных значений сверток, в силу чего для каждого значения свертки имеется большое множество прообразов, то есть сообщений с заданным значением хеш-функции. Заметим, что при случайном и равновероятном выборе сообщений условие равномерности распределения значений хеш-функции эквивалентно наличию одинакового числа прообразов для каждого значения свертки.
Как правило, хеш-функции строят на основе так называемых одношаговых сжимающихся функций 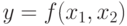 двух переменных, где
двух переменных, где  и
и  - двоичные векторы длины
- двоичные векторы длины  и
и  соответственно, и
соответственно, и  - длина свертки. Для получения значения
- длина свертки. Для получения значения 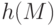 сообщение
сообщение  сначала разбивается на блоки длины
сначала разбивается на блоки длины  (при этом если длина сообщения не кратна
(при этом если длина сообщения не кратна  , то последний блок неким специальным образом дополняется до полного), а затем к полученным блокам
, то последний блок неким специальным образом дополняется до полного), а затем к полученным блокам 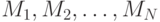 применяют следующую последовательную процедуру вычисления свертки:
применяют следующую последовательную процедуру вычисления свертки:
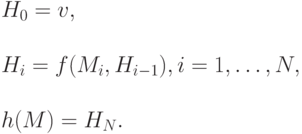
Здесь  - некоторый фиксированный начальный вектор. Если функция
- некоторый фиксированный начальный вектор. Если функция  зависит от ключа, то этот вектор можно положить равным нулевому вектору. Если же функция
зависит от ключа, то этот вектор можно положить равным нулевому вектору. Если же функция  не зависит от ключа, то для исключения возможности перебора коротких сообщений (при попытках обращения хеш-функции) этот вектор можно составить из фрагментов указывающих на дату, время, номер сообщения и т.п.
не зависит от ключа, то для исключения возможности перебора коротких сообщений (при попытках обращения хеш-функции) этот вектор можно составить из фрагментов указывающих на дату, время, номер сообщения и т.п.
При таком подходе свойства хеш-функции  полностью определяются свойствами одношаговой сжимающей функции
полностью определяются свойствами одношаговой сжимающей функции  .
.
9.2 Электронная подпись
9.2.1 Общие положения
Появление криптографии с открытым ключом позволило решать задачи, которые ранее считались неразрешимыми. К таким задачам относится использование цифрового аналога собственноручной подписи абонента - электронной цифровой подписи (ЭЦП).
Цифровая подпись (ЭЦП) для сообщения является числом, зависящим от самого сообщения и от секретного ключа, известного только подписывающему. Важное требование: подпись должна допускать проверку без знания секретного ключа. При возникновении спорной ситуации, связанной с отказом от факта подписи либо с возможной подделкой подписи, третья сторона должна иметь возможность разрешить спор.
Задачи, которые решает подпись:
- Осуществить аутентификацию источника сообщения,
- Установить целостность сообщения,
- Обеспечить невозможность отказа от факта подписи конкретного сообщения.
Для реализации схемы ЭЦП необходимы два алгоритма: алгоритм генерации подписи и алгоритм проверки. Надежность схемы ЭЦП определяется сложностью следующих задач:
- Подделки подписи, то есть нахождения правильного значения подписи для заданного документа,
- Создания подписанного сообщения, то есть нахождения хотя бы одного сообщения с правильным значением подписи,
- Подмены подписи, то есть нахождения двух различных сообщений с одинаковым значением подписи.
Заметим, что между ЭЦП и собственноручной подписью имеются различия, хотя они и служат для решения одинаковых задач. Так, ЭЦП зависит от подписываемого текста, различна для разных тестов. Кроме того, ЭЦП требует дополнительных механизмов, реализующих алгоритмы ее вычисления и проверки. Наконец, принципиальной сложностью, возникающей при использовании ЭЦП, является необходимость создания инфраструктуры открытых ключей. Эта инфраструктура состоит из центров сертификации открытых ключей и обеспечивает возможность своевременного подтверждения достоверности открытой информации, необходимой для проверки ЭЦП, что необходимо для предотвращения подделки подписи.
Некоторые наиболее употребительные схемы ЭЦП
В настоящее время имеется большое количество различных схем ЭЦП, обеспечивающих тот или иной уровень стойкости. Существующие схемы можно классифицировать таким образом:
- Схемы на основе систем шифрования с открытыми ключами,
- Схемы со специально разработанными алгоритмами вычисления и проверки подписи,
- Схемы на основе симметричных систем шифрования. Рассмотрим некоторые схемы.
9.2.2 Схема Эль-Гамаля
См. [1]
Безопасность схемы основана на трудности вычисления дискретных логарифмов в конечном поле. Для генерации пары ключей выбирается простое число  и два случайных числа,
и два случайных числа,  и
и  , оба меньше
, оба меньше  . Затем вычисляется
. Затем вычисляется 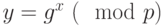 . Открытым ключом является набор чисел
. Открытым ключом является набор чисел 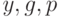 . При этом
. При этом  и
и  можно сделать общими для группы пользователей. Секретным ключом является
можно сделать общими для группы пользователей. Секретным ключом является  . Чтобы подписать сообщение
. Чтобы подписать сообщение  , сначала выбирается случайное число
, сначала выбирается случайное число  , взаимно простое с
, взаимно простое с  . Затем вычисляются подпись
. Затем вычисляются подпись 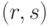 по формулам:
по формулам:
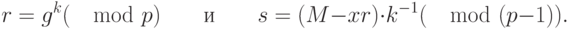
Для проверки подписи нужно убедиться, что
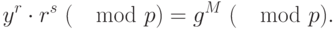
Первое замечание о выборе  . Оно должно храниться в секрете и уничтожаться сразу после вычисления подписи, так как знание
. Оно должно храниться в секрете и уничтожаться сразу после вычисления подписи, так как знание  и значения подписи позволяет легко вычислить секретный ключ
и значения подписи позволяет легко вычислить секретный ключ  . И тогда подпись будет полностью скомпрометирована. Кроме того,
. И тогда подпись будет полностью скомпрометирована. Кроме того,  должно быть действительно случайным и не должно повторяться для различных подписей, полученных на одном секретном ключе. Если злоумышление сможет получить два сообщения, подписанные с помощью одного и того же значения
должно быть действительно случайным и не должно повторяться для различных подписей, полученных на одном секретном ключе. Если злоумышление сможет получить два сообщения, подписанные с помощью одного и того же значения  , то он сможет раскрыть
, то он сможет раскрыть  , даже не зная значение
, даже не зная значение  .
.
Схема Эль-Гамаля послужила образцом для построения большого семейства во многом сходных по своим свойствам схем подписи.
Пример 9.1 Выберем 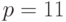 и
и  , а секретный ключ
, а секретный ключ 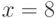 .
.
Вычислим:
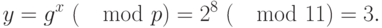
Открытым ключом являются  ,
,  и
и 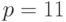 . Чтобы подписать
. Чтобы подписать 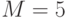 , сначала выберем случайное число
, сначала выберем случайное число  , убеждаемся, что
, убеждаемся, что  . Вычисляем:
. Вычисляем:

Теперь находим
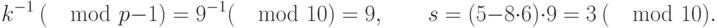
Итак, подпись представляет собой пару: 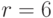 и
и 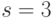 .
.
Для проверки подписи убедимся, что:
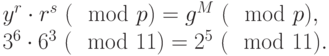
Второе замечание. При вычислении подписи целесообразно использовать хэш-образ сообщения, а не само сообщение  . Это защитит схему подписи от возможности подбора сообщений с известным значением подписи. Это распространенная практика. В приведенном примере можно считать, что
. Это защитит схему подписи от возможности подбора сообщений с известным значением подписи. Это распространенная практика. В приведенном примере можно считать, что 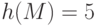 . Наиболее распространена технология ЭЦП, основанная на совместном применении алгоритмов хеширования и шифрования с открытым ключом (в частности, RSA или Эль-Гамаля).
. Наиболее распространена технология ЭЦП, основанная на совместном применении алгоритмов хеширования и шифрования с открытым ключом (в частности, RSA или Эль-Гамаля).
Алгоритм формирования подписи выглядит следующим образом:
-
Пусть
 - подписываемое сообщение. Отправитель вычисляет хеш-значение подписываемого сообщения
- подписываемое сообщение. Отправитель вычисляет хеш-значение подписываемого сообщения 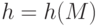 . Значение
. Значение  должно удовлетворять неравенству
должно удовлетворять неравенству 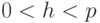 .
. - Отправитель выбирает случайное число
 ,
, 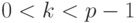 , взаимно простое с
, взаимно простое с  , и вычисляет числа:
, и вычисляет числа:
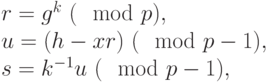
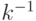 - число, обратное
- число, обратное  по модулю
по модулю  ,
, 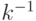 существует, так как
существует, так как  и
и  - взаимно просты.
- взаимно просты. - Подпись
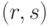 добавляется к сообщению, и тройка
добавляется к сообщению, и тройка 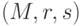 передается получателю.
передается получателю.
Проверка подписи: получатель заново вычисляет хеш-значение присланного сообщения 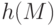 и проверяет подпись, используя равенство:
и проверяет подпись, используя равенство:
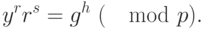
Если подпись верна, то это равенство выполняется.
Отметим, что число  выбирается заново для каждого нового сообщения и должно держаться в секрете.
выбирается заново для каждого нового сообщения и должно держаться в секрете.
Используемые на практике алгоритмы хеширования достаточно сложны, поэтому будем использовать учебные алгоритмы формирования хеш-значения 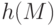 . Схему учебных алгоритмов хэширования предложила Васильева И.Н. [1].
. Схему учебных алгоритмов хэширования предложила Васильева И.Н. [1].
Первый учебный алгоритм хеширования
Входом для данного алгоритма является строка, состоящая из букв русского языка.
-
Выбирается число
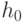 - вектор инициализации. Число
- вектор инициализации. Число 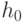 равно длине сообщения в символах.
равно длине сообщения в символах. -
Для каждого символа сообщения вычисляется значение
 , где
, где 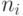 - номер
- номер  -й буквы сообщения в алфавите. Для удобства вычислений ниже приведен нумерованный алфавит.
-й буквы сообщения в алфавите. Для удобства вычислений ниже приведен нумерованный алфавит. - Значение
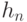 , вычисленное для последнего символа, является хеш-значением сообщения:
, вычисленное для последнего символа, является хеш-значением сообщения: 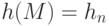 .
.
Следует отметить, что вычисленное по этому алгоритму хеш-значение зависит от всех символов сообщения  .
.
Известны значения общих параметров системы Эль-Гамаля: 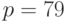 ,
, 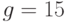 , личный ключ абонента
, личный ключ абонента  и случайное число
и случайное число  , выбранное для формирования подписи сообщения. Для заданного текстового сообщения
, выбранное для формирования подписи сообщения. Для заданного текстового сообщения  сгенерировать цифровую электронную подпись по алгоритму Эль-Гамаля.
сгенерировать цифровую электронную подпись по алгоритму Эль-Гамаля.
Пример 9.2 Выполнить вычисление и проверку подписи сообщения  по алгоритму Эль-Гамаля. Использовать параметры подписи:
по алгоритму Эль-Гамаля. Использовать параметры подписи:

- Сформируем хэш-сумму сообщения. Начальное значение
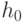 равно количеству символов сообщения:
равно количеству символов сообщения:  . Далее,
. Далее,

- Вычисляем число
 по формуле
по формуле 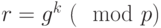 . Для рассматриваемого примера получили:
. Для рассматриваемого примера получили:

- Вычисляем число
 по формуле
по формуле 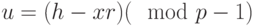 , для рассматриваемого примера
, для рассматриваемого примера
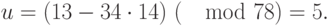
- Вычисляем значение
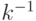 по модулю
по модулю  с помощью расширенного алгоритма Евклида. Для рассматриваемого примера значение
с помощью расширенного алгоритма Евклида. Для рассматриваемого примера значение  .
.
Примечание: если полученное значение
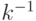 - отрицательное, следует взять его по модулю
- отрицательное, следует взять его по модулю  .
. - Вычисляем число
 по формуле
по формуле 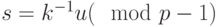 . В примере
. В примере

- Цифровая подпись сообщения для рассматриваемого примера:
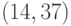 .
.
Для проверки правильности вычисления полученной цифровой подписи следует произвести ее проверку с помощью открытого ключа абонента и убедиться, что подпись подлинная.
- Сформируем открытый ключ
 абонента по формуле
абонента по формуле 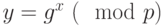 :
:
Для рассматриваемого примера
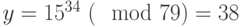 .
. -
Аналогичным образом вычисляем значения
В примере получаем: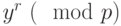 и
и  , а затем их произведение по модулю
, а затем их произведение по модулю  .
.
- Вычисляем значение
 , значение
, значение  было получено ранее.
было получено ранее.
В примере
 .
. - Проверяем выполнение равенства
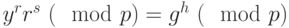 , если равенство выполняется - подпись подлинная, то есть она была вычислена правильно.
, если равенство выполняется - подпись подлинная, то есть она была вычислена правильно.
В примере получили
 , равенство выполняется, значит, подпись сгенерирована правильно.
, равенство выполняется, значит, подпись сгенерирована правильно.
Второй учебный алгоритм хеширования
В этом алгоритме  - простое число, которое затем будем модулем для алгоритма цифровой подписи Эль-Гамаля. Теперь сообщение
- простое число, которое затем будем модулем для алгоритма цифровой подписи Эль-Гамаля. Теперь сообщение  - число, записанное в десятичной системе счисления.
- число, записанное в десятичной системе счисления.
-
Начальное значение
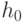 принимается равным числу десятичных разрядов в
принимается равным числу десятичных разрядов в  .
. - Для каждого десятичного знака
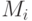 числа
числа  вычисляется значение
вычисляется значение
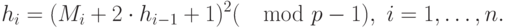
- Значение
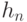 , вычисленное для последнего символа, увеличенное на 1, является хеш-значением сообщения:
, вычисленное для последнего символа, увеличенное на 1, является хеш-значением сообщения:  .
.
Вычисленное по этому алгоритму хеш-значение зависит от всех символов сообщения  .
.
Пример 9.3 Известны значения общих параметров системы Эль-Гамаля: 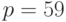 ,
, 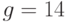 и открытый ключ абонента
и открытый ключ абонента 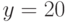 . От абонента получено сообщение
. От абонента получено сообщение 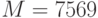 , снабженное цифровой подписью Эль-Гамаля
, снабженное цифровой подписью Эль-Гамаля 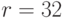 ,
, 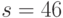 . Проверить подлинность цифровой подписи. Хеш-значение сообщение вычисляется с помощью второго учебного алгоритма.
. Проверить подлинность цифровой подписи. Хеш-значение сообщение вычисляется с помощью второго учебного алгоритма.
-
Вычисляем значения
В рассматриваемом примере получаем: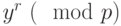 и
и  , а затем их произведение по модулю
, а затем их произведение по модулю  :
: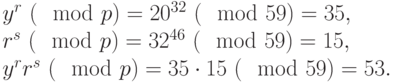
- Для полученного сообщения вычисляем хеш-значение
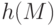 по второму учебному алгоритму.
по второму учебному алгоритму.
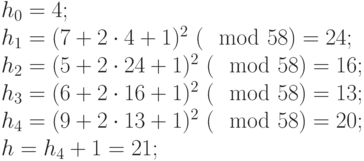
- Вычисляем значение
 .
.
В примере
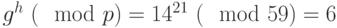 .
. - Проверяем выполнение равенства
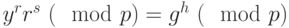 , если равенство выполняется - подпись подлинная, в противном случае - фальшивая.
, если равенство выполняется - подпись подлинная, в противном случае - фальшивая.
В нашем примере
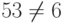 . Равенство не выполняется, значит, подпись фальшивая.
. Равенство не выполняется, значит, подпись фальшивая.

