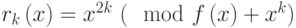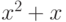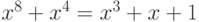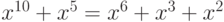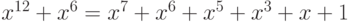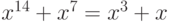НОУ ИНТУИТ | Криптографические методы защиты информации. Лекция 3: Алгебраические системы

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 02.03.2017 | Уровень: для всех | Доступ: свободно

|

Вам нравится? Нравится 55 студентам

| Поделиться |

Поддержать программу

3.3 Поля конечного непростого порядка

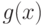Для полиномов справедлив аналог теоремы о делении с остатком. Для любых полиномов f(x) и g(x) существуют полиномы 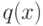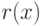q(x) , r(x) , такие, что

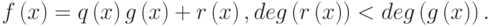
$f\left(x\right)=q\left(x\right)g\left(x\right)+r\left(x\right),{deg}\left(r\left(x\right)\right)<{deg}\left(g\left(x\right)\right).$

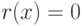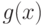Если r(x) = 0 , то g(x) называется делителем многочлена f(x) .

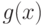Определение 3.23 Наибольшим общим делителем многочленов и называется их общий делитель, который делится на любой другой их общий делитель.

Для полиномов наибольший общий делитель определён с точностью до умножения на константу. Будем всегда выбирать полином с единичным старшим членом. Полином, не имеющий нетривиальных делителей, называется неприводимым.

Определение 3.24 Более точно, полином степени над полем называется неприводимым, если не существует двух таких полиномов 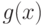, 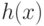степеней меньших , что .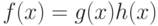

В качестве примера рассмотрим алгоритм формирования контрольной суммы CRC (Cyclic Redundancy Code). Он используется для того, чтобы при передаче сообщения через подверженные помехам каналы выявлять ошибки передачи данных. Контрольная сумма передаётся вместе с данными, а затем принимающая сторона также вычисляет контрольную сумму и сравнивает её с принятой.

Для формирования контрольной суммы биты данных представляются как коэффициенты полинома над полем 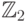$\mathbb{Z}_2$ . Затем вычисляется остаток от деления этого полинома на некоторый фиксированный полином, называемый порождающим. Остаток от деления - снова полином, коэффициенты которого вновь рассматриваются как биты некоторого числа, являющегося контрольной суммой.

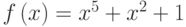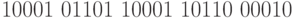Пример 3.10 Используя порождающий полином $f\left(x\right)={x}^{5}+{x}^{2}+1$ , построить контрольную сумму сообщения: $10001\ 01101\ 10001\ 10110\ 00010$ .

Решение. Представим сообщение в виде:

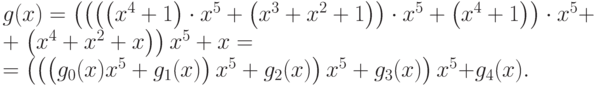
$g(x)=\left(\left(\left(\left({x}^{4}+1 \right) \cdot {x}^{5}+ \left({x}^{3}+{x}^{2}+1\right)\right) \cdot {x}^{5}+\left({x}^{4}+1 \right)\right) \cdot {x}^{5}+\right.\\ +\left.\left({x}^{4}+{x}^{2}+x\right)\right){x}^{5}+x= \\ =\left(\left(\left(g_{0}(x){x}^{5}+{g}_{1}(x)\right){x}^{5}+{g}_{2}(x) \right){x}^{5}+{g}_{3}(x)\right){x}^{5}+{g}_{4}(x).$

Обозначим 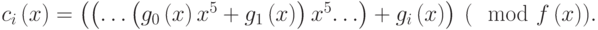${c}_{i}\left(x\right)=\left(\left({\dots}\left({g}_{0}\left(x\right){x}^{5}+{g}_{1}\left(x\right)\right){x}^{5}{\dots}\right)+{g}_{i}\left(x\right)\right)~(\mod f\left(x\right)).$

Очевидно, 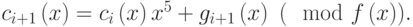${c}_{i+1}\left(x\right)={c}_{i}\left(x\right){x}^{5}+{g}_{i+1}\left(x\right)~(\mod f\left(x\right)).$

По модулю f(x) имеем:

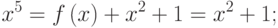
${x}^{5}=f\left(x\right)+{x}^{2}+1={x}^{2}+1;$

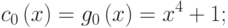
${c}_{0}\left(x\right)={g}_{0}\left(x\right)={x}^{4}+1;$

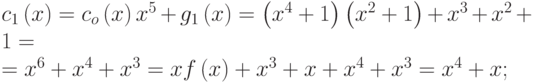
${c}_{1}\left(x\right)={c}_{o}\left(x\right){x}^{5}+{g}_{1}\left(x\right)= \left({x}^{4}+1\right)\left({x}^{2}+1\right)+{x}^{3}+{x}^{2}+1=\\ ={x}^{6}+{x}^{4}+{x}^{3}=xf\left(x\right)+{x}^{3}+x+{x}^{4}+{x}^{3}={x}^{4}+x;$

${c}_{2}\left(x\right)={c}_{1}\left(x\right){x}^{5}+{g}_{2}\left(x\right)=\left({x}^{4}+x\right)\left({x}^{2}+1\right)+{x}^{4}+1=\\ ={x}^{6}+{x}^{3}+x+1={xf}\left(x\right)+1=1;$

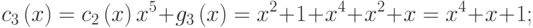
${c}_{3}\left(x\right)={c}_{2}\left(x\right){x}^{5}+{g}_{3}\left(x\right)={x}^{2}+1+{x}^{4}+{x}^{2}+x={x}^{4}+x+1;$

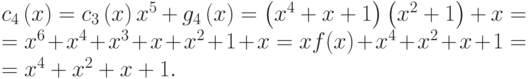
${c}_{4}\left(x\right)={c}_{3}\left(x\right){x}^{5}+{g}_{4}\left(x\right)=\left({x}^{4}+x+1\right)\left({x}^{2}+1\right)+x=\\ ={x}^{6}+{x}^{4}+{x}^{3}+x+{x}^{2}+1+x=x f(x)+{x}^{4}+{x}^{2}+x+1=\\ ={x}^{4}+{x}^{2}+x+1.$

Поэтому контрольная сумма равна (10111).

Пример 3.11 По каналу сначала была передана контрольная сумма сообщения 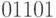, а затем начало передаваться сообщение. Злоумышленник смог испортить сообщение, и его контрольная сумма стала . Какие биты должен злоумышленник присоединить к хвосту сообщения, чтобы контрольная сумма совпала с переданной пользователю?

Решение. Имеем: 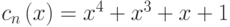${c}_{n}\left(x\right)={x}^{4}+{x}^{3}+x+1$ , при этом требуется, чтобы 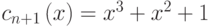${c}_{n+1}\left(x\right)={x}^{3}+{x}^{2}+1$ . В то же время:

${c}_{n+1}\left(x\right)={c}_{n}\left(x\right) \cdot {x}^{5}+{g}_{n+1}\left(x\right).$

Злоумышленник всего-навсего должен нужным образом подобрать 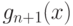${g}_{n+1}(x)$ :

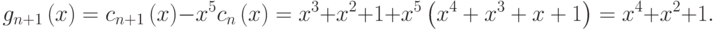
${g}_{n+1}\left(x\right)={c}_{n+1}\left(x\right)-{x}^{5}{c}_{n}\left(x\right)={x}^{3}+{x}^{2}+1+{x}^{5}\left({x}^{4}+{x}^{3}+x+1\right)={x}^{4}+{x}^{2}+1.$

Итак, злоумышленник должен отправить 5 бит: 10101, и контрольная сумма испорченного сообщения совпадёт с контрольной суммой, которую ожидает пользователь.

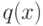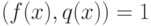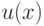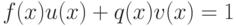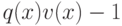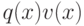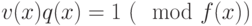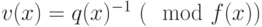Если полином f(x) неприводим, то для любого полинома q(x) степени меньше имеем $\GCD(f(x), q(x)) = 1$ . Выполнив расширенный алгоритм Евклида, мы можем найти такие многочлены u(x) , v(x) , что f(x) u(x) + q(x) v(x) = 1 . Очевидно, тогда q(x)v(x) - 1 лежит в идеале f(x) F[x] всех многочленов, кратных f(x) , а - в смежном классе, содержащем единицу. Другими словами, $v(x)q(x) = 1 ~(\mod f(x))$ , или $v(x) = q(x)^{- 1} ~(\mod f(x))$ .

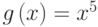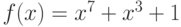Пример 3.12 Найти в кольце $\mathbb{Z}_2[x]$ полином, обратный к полиному $g\left(x\right)={x}^{5}$ по модулю $f(x)=x^{7}+{x}^{3}+1$ .

Решение. Выполним расширенный алгоритм Евклида. Положим 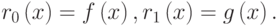${r}_{0}\left(x\right)=f\left(x\right),{r}_{1}\left(x\right)=g\left(x\right).$

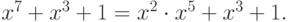${x}^{7}+{x}^{3}+1={x}^{2} \cdot {x}^{5}+{x}^{3}+1.$ Отсюда ${r}_{2}\left(x\right)={x}^{3}+1={r}_{0}\left(x\right)+{x}^{2}{r}_{1}\left(x\right).$
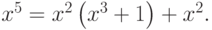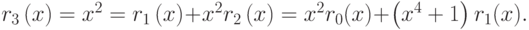
${x}^{5}={x}^{2}\left({x}^{3}+1\right)+{x}^{2}.$ Отсюда ${r}_{3}\left(x\right)={x}^{2}={r}_{1}\left(x\right)+{x}^{2}{r}_{2}\left(x\right)={x}^{2}{r}_{0}(x)+\left({x}^{4}+1\right){r}_{1}(x).$
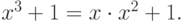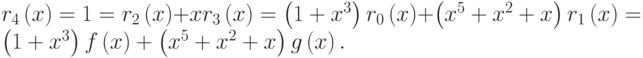
${x}^{3}+1=x \cdot {x}^{2}+1.$ Отсюда ${r}_{4}\left(x\right)=1={r}_{2}\left(x\right)+x{r}_{3}\left(x\right)=\left(1+{x}^{3}\right){r}_{0}\left(x\right)+\left({x}^{5}+{x}^{2}+x\right){r}_{1}\left(x\right)=\left(1+{x}^{3}\right)f\left(x\right)+\left({x}^{5}+{x}^{2}+x\right)g\left(x\right).$

Следовательно, 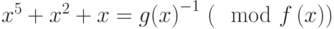${x}^{5}+{x}^{2}+x=g{\left(x\right)}^{-1}~(\mod f\left(x\right))$ .

Более подходящим для программной реализации будет следующее описание расширенного алгоритма Евклида:

Вход: полиномы 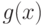f(x) , g(x) , степень f(x) не меньше степени g(x) .

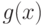Выход: полиномы 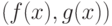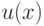$\GCD(f(x),g(x))$ , u(x) и v(x) такие, что $\GCD(f(x),g(x)) = u(x) f(x) + v(x) g(x)$ .

Полагаем , , , , .
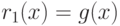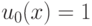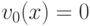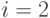Выполняем деление с остатком: $r_{i-2}(x) = q(x) r_{i-1}(x) + r_i(x)$ .
Если 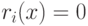, то положить 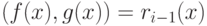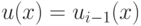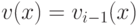$\GCD(f(x), g(x)) = r_{i-1}(x)$ , $u(x) = u_{i-1}(x)$ , $v(x)=v_{i-1}(x)$ и выйти.
Положить 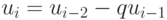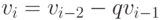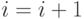$u_i = u_{i-2} -qu_{i-1}$ , $v_i = v_{i-2}-qv_{i-1}$ , и перейти к шагу 2.

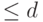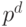Когда полином f(x) над полем степени неприводим, множество полиномов над степени $\leq d$ относительно сложения и умножения по модулю f(x) образуют поле. Известно, что над полем простого порядка существуют неприводимые многочлены любой степени. Поэтому описанным способом можно построить поля любого порядка p^d . Построение неприводимых полиномов является важной задачей.

Поскольку все поля одинакового порядка изоморфны, для поля данного порядка вводится единое обозначение: GF(q) .

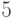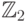Пример 3.13 Построить неприводимый полином степени над $\mathbb{Z}_2$ .

Решение. Пока нам неизвестен более быстрый метод, будем использовать метод пробных делений. Если полином степени 5 приводим, то один из его сомножителей является неприводимым и имеет степень меньше 3. Полиномы степени меньше 3: , 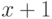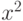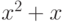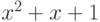x + 1 , x^2 , x^2+x , x^2+1 , x^2+x+1 . Из них неприводимыми являются , x + 1 , x^2 + x + 1 .

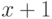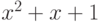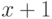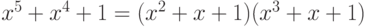Выберем случайно полином. Пусть им оказался x^5+x^4+1 . Он не делится на и на x + 1 , так как 0 и 1 не являются его корнями. Однако x^5+x^4+1 = (x^2+x+1)(x^3+x+1) .

Пусть случайно выбран полином 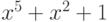x^5+x^2+1 . Снова, 0 и 1 не являются его корнями, и 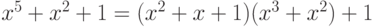x^5+x^2+1=(x^2+x+1)(x^3+x^2)+1 . Следовательно, этот полином неприводим.

3.3.1 Алгоритм Берлекемпа

Разумеется, существуют более простые способы тестирования полиномов над конечным полем на приводимость, например, алгоритм Берлекемпа [1].

Вход: полином f(x) степени над конечным полем , не имеющий кратных корней (что проверяется вычислением его наибольшего общего делителя с производной f'(x) .

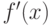Выход: ответ на вопрос - приводим ли многочлен.

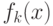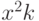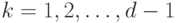Вычислить - остаток от деления на , $k=1,2,\ldots,d-1$ .
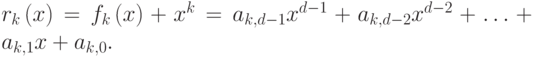
Вычислить ${r}_{k}\left(x\right)={f}_{k}\left(x\right)+{x}^{k}={a}_{k,d-1}{x}^{d-1}+{a}_{k,d-2}{x}^{d-2}+{\dots}+{a}_{k,1}x+{a}_{k,0}.$
Вычислить - ранг матрицы
$\left[\begin{matrix}{a}_{k,d-1}&{\cdots}&{a}_{k,0}\\ \vdots &\ddots & \vdots \\{a}_{1,d-1}&{\cdots}&{a}_{1,0} \end{matrix}\right].$
Полином приводим тогда и только тогда, когда .

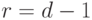Пример 3.14 Протестировать на приводимость полином 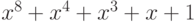${x}^{8}+{x}^{4}+{x}^{3}+x+1$ .

Решение. Вычислим, согласно алгоритму, остатки от деления

	${r}_{k}\left(x\right)={x}^{2k}~(\mod f\left(x\right)+{x}^{k})$
1	${x}^{2}+x$
2	${x}^{4}+{x}^{2}$
3	${x}^{6}+{x}^{3}$
4	${x}^{8}+{x}^{4}={x}^{3}+x+1$
5	${x}^{10}+{x}^{5}={x}^{6}+{x}^{3}+{x}^{2}$
6	${x}^{12}+{x}^{6}={x}^{7}+{x}^{6}+x^{5}+{x}^{3}+x+1$
7	${x}^{14}+{x}^{7}={x}^{3}+x$

Построим и приведём к трапецеидальному виду матрицу коэффициентов этих полиномов:

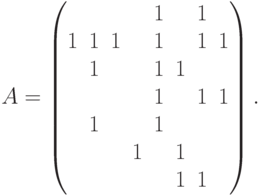
$A=\left(\begin{matrix} & & & & 1 & & 1 & \\ 1& 1& 1& & 1 & & 1 & 1 \\ & 1& & & 1 & 1& & \\ & & & & 1& &1 &1\\ & 1& & & 1 & & & \\ & & & 1& & 1& & \\ & & & & & 1& 1 & \\ \end{matrix}\right).$

Переместим вторую строку на первое место, третью строку - на второе, шестую - на третье, далее пойдут по порядку первая, четвертая, сумма пятой и третьей строк, седьмая строка. Имеем:

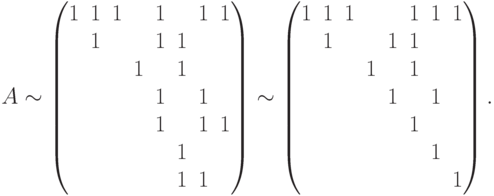
$A\sim \left(\begin{matrix} 1& 1& 1& & 1& & 1 & 1\\ & 1& & & 1 & 1& & \\ & & &1 & & 1& & \\ & & & & 1& &1 & \\ & & & & 1 & & 1 &1\\ & & & & & 1& & \\ & & & & & 1& 1 & \\ \end{matrix}\right)\sim \left( \begin{matrix} 1& 1& 1& & & 1& 1 & 1\\ & 1& & & 1 & 1& & \\ & & &1 & & 1& & \\ & & & & 1& &1 & \\ & & & & &1 & & \\ & & & & & &1 & \\ & & & & & & &1\\ \end{matrix}\right).$

Итак, ранг матрицы равен 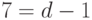7 = d - 1 , следовательно, полином неприводим.

Список литературы

Berlekamp, E. R. Factoring Polynomials Over Finite Fields // Bell System Technical Journal 46(1967). - p. 1853-1859.

Дальше >>

Системное администрирование 1500

Криптографические методы защиты информации