НОУ ИНТУИТ | Введение в математику. Практикум. Лекция 4: Векторные величины, преобразования и пространства

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 22.01.2008 | Уровень: для всех | Доступ: платный

|

Вам нравится? Нравится 47 студентам

| Поделиться |

Поддержать программу

Аннотация: Развитие исследовательских и творческих навыков по использованию векторов, векторных величин и преобразований, линейных пространств

Ключевые слова: вектор, скалярное произведение, коллинеарность, метрика, норма

Исследовать на разрешимость векторное уравнение (уравнение с неизвестным вектором ): (x,a)=1, где x=(x₁;x₂) – неизвестный вектор, а=(1;2) – известный вектор, коллинеарный вектору x, (x,a) – их скалярное произведение. Какое скалярное уравнение (какие скалярные уравнения) можно связать с этим векторным уравнением? Найти решение. Указание: использовать условие коллинеарности двух векторов и скалярное произведение двух векторов, выраженных в координатной форме.
Пусть дан некоторый технологический процесс, включающий в себя n продуктов, причем, если продукт i потребляется, то с ним связывается некоторое отрицательное число (темп потребления продукта), а если продукт производится, то с ним связывается положительное число (темп производства продукта). Пусть в производстве n продуктов используется набор таких технологических процессов: А₁, А₂, ..., А_m, количество продукта (производимого или потребляемого) j -го вида в i -ом процессе (i=1, 2,..., m; j=1, 2,...,n) обозначим a_ij. Описать структуру и темп некоторого конкретного производства и потребления с помощью матрицы вида A(mxn). Поставить одну задачу на нахождение решения системы уравнений. Указание: можно сформулировать, например, задачу поиска такого объема и структуры производства (неизвестных x_i ) для которых при заданном темпе произ водства достигается баланс.
Многие геометрические преобразования можно задавать соответствующими матрицами (преобразований). Рассмотрим стандартное линейное преобразование плоскости (плоской фигуры) определяемую матрицей, причем мы будем рассматривать не прямоугольную систему координат, а "косоугольную". Например, матрица

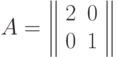
$A=\left \| \begin{array}{cc}2&0\\ 0&1\end{array}\right\|$

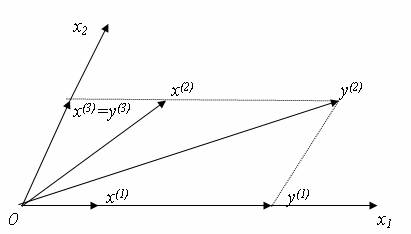
определяет на плоскости (x₁,x₂) линейное преобразование рассматриваемого вида, а именно, растяжение плоскости вдоль оси Ох₁ в 2 раза (см. рис. 1). Здесь х⁽¹⁾, х⁽²⁾ – векторы до деформации, а у⁽¹⁾, у⁽²⁾ – их образы, полученные в результате линейного преобразования по приведенным формулам.

Рис. 1. Преобразование растяжения и сжатия на плоскости

Записать матрицу сжатия по оси х₁ в 2 раза и растяжения по оси х₂ в 3 раза. Указание: выпишите связи между новыми (после преобразования) и "старыми" (до преобразования) координатами (осями).
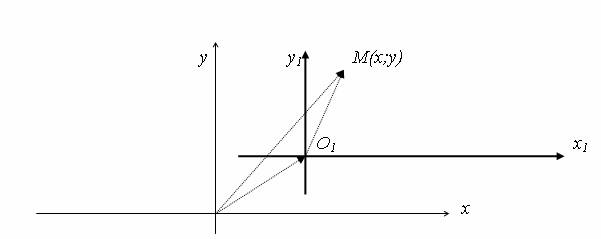
Так же можно задать и другое базовое геометрическое преобразование – параллельный перенос на плоскости. Пусть задана "старая" система координат хОу, О(0;0) и "новая" – ХО₁У, О₁(х₀;у₀), где оси координат параллельны между собой: x₁||x, y₁||y (рис. 2).

Рис. 2. Параллельный перенос на плоскости

Запишите это преобразование в матричной форме. Указание: выпишите связи между новыми (после преобразования) и "старыми" (до преобразования) координатами (осями) или

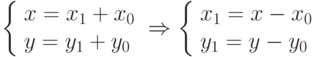
$\left\{ \begin{array}{l}x=x_1+x_0\\ y=y_1+y_0\end{array}\right \Rightarrow \left\{ \begin{array}{l}x_1=x-x_0\\ y_1=y-y_0\end{array}\right$
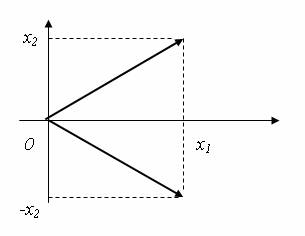
В прямоугольной системе координат запишите в матричном виде зеркальное отражение точек плоскости х₁Ox₂. Указание: зеркальное отображение относительно оси х₁ может быть изображено, например, как на рисунке ниже.

Рис. 3. Зеркальное отображение относительно Ох
Осуществите в прямоугольной системе координат преобразование, задаваемое матрицей

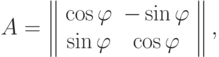
$A= \left\| \begin{array}{cc}\cos\varphi & -\sin \varphi \\ \sin\varphi & \cos\varphi \end{array}\right\|,$

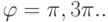где $\phi$ - произвольный угол. Что происходит в случаях $\varphi =2\pi , 4\pi , ..$ .? Чему равна матрица А в этих случаях? Что происходит в случаях $\varphi =\pi , 3\pi ..$ .? Чему равна матрица А в этих случаях? Каким образом связано это преобразование с гармонией и структурированностью окружающего нас мира? Указание: случай $\varphi =\pi , 2\pi ,4\pi , ..$ .? соответствует тождественному преобразованию (матрица А=Е ); при $\varphi =\pi , 3\pi , 5\pi , ..$ . преобразование изменяет направления векторов на противоположное (такое преобразование называется центральной симметрией).
Свободное время для творческого развития личности, можно рассматривать (несколько упрощенно) как процесс в 5 -мерном пространстве следующих измерений:
1. x₁ – "технологические условия производства",
2. x₂ – "число рабочих",
3. x₃ – "время работы",
4. x₄ – "заработная плата",
5. x₅ – "социально-экономические условия труда".
Определите аналогично 10 -мерное пространство. Указание: добавьте к "старым координатам" еще 5 новых.
Прямая – пространство размерности 1 (измерение – длина). "Обитатели" этого пространства всех "остальных" видят как точки, т.е. "никого равного себе не хотят видеть", все – эгоисты. Плоскость – пространство размерности 2 (ширина, длина). "Обитатели" этого пространства всех остальных "видят" лишь в виде отрезков и точек т.е. "всех видят ниже себя", все – надменны. Проведите аналогии в трехмерном и четырехмерном пространствах. Указание: четырехмерный объект можно представить эскизно своими трехмерными проекциями, аналогично тому, как трехмерный объект можно представить своими тремя проекциями на координатные плоскости.
Пространство (обозначаемое как С[a;b] ) всех непрерывных на [a;b] функций, т.е. C([a;b]) ={ $f(x): x\in [a;b], f(x)$ – непрерывна}. Операции в этом пространстве можно определить как операции над функциями. Проверьте аксиомы линейного пространства. Указание: любым двум функциям f(x), $g(x)\in C[a;b]$ можно сопоставить их сумму: s(x)=f(x)+g(x), $s(x)\in C[a;b]$ , а так как сумма двух непрерывных функций по свойству непрерывных функций – функция непрерывная, то эта операция не выводит никогда за пределы данного пространства; умножение на число функции – аналогично не выводит за пределы пространства.
В пространстве С[a;b] выясните, что может являться нулем, единицей. Введите метрику и норму корректным способом и проверьте аксиомы метрического и нормированного пространства. Вычислите расстояние между функциями x=t, y=sin(t), a=0, b=1. Найдите нормы этих двух функций. Указание: метрику можно определить, например, как 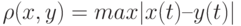$\rho (x,y)=max|x(t)–y(t)|$ , а норму – как ||x||=max|x(t)|, где максимум берется по всему отрезку [a;b].