НОУ ИНТУИТ | Введение в математику. Практикум. Лекция 4: Совокупности и отношения

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 22.01.2008 | Уровень: для всех | Доступ: платный

|

Вам нравится? Нравится 47 студентам

| Поделиться |

Поддержать программу

Аннотация: Решение типовых задач на множества, кортежи, функции, отношения, обучение реферированию и Интернет–поиску по этой теме

Ключевые слова: множество, элемент множества, функция, график, четность, периодичность, отношение

Задачи

Привести примеры множеств числовой и нечисловой природы. Образовать из них различные кортежи, в том числе, имеющие семантическое и прагматическое значение (смысл). Указание: например, использовать пары (<объект>, <числовая характеристика объекта>).
Получите и запишите словесно закон формирования элементов множеств:

Х={2, 4,..., 100}, Y={1,3,..., 99}, Z={1,1/2, 1/4, 1/8, ..., 1/128}.

Указание: использовать свойства прогрессии.
Записать аналитически законы образования элементов множеств, найденных для предыдущей задачи в словесном виде. Указание: использовать формулы общего члена прогрессии.
Запишите аналитически функцию и нарисуйте график кусочно-заданной функции, принимающей на отрезке [–1;2] значения равные квадрату аргумента, а на промежутке (2;5] – значения, равные синусу от значения аргумента. Указание: на отрезке [–1;2] имеем y=x².
Нарисуйте графики трех функции: y=x², y=x³+6, y=-x²-3. Найдите функции, обратные к ним. Указание: для первой функции $x=\pm \sqrt{y}$ состоит из двух ветвей.
Выяснить, монотонна ли функция 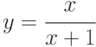$y=\cfrac{x}{x+1}$ ? Обосновать ответ. Построить ее график. Указание: определить знак производной.
Выяснить четность или нечетность функции $y=\cfrac{x}{x^2+1}$ . Обосновать ответ. Построить график функции. Указание: условие четности функции y(–x) = y(x).
Выяснить периодичность функции 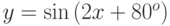$y=\sin{(2x+80^o)}$ . Обосновать ответ. Найти период. Построить график. Указание: период Т функции удовлетворят соотношению y(–x) = y(x+Т) для каждого аргумента.
Построить график функции u=x²+y²+z²–9. Указание: построить проекции на координатные плоскости.
Построить график y=2(x²+6x–8)+sin(3x–90^o). Указание: Использовать "опорные" графики функций y=x², y=sin(x).