Уравнения и неравенства

Задачи

1. Найти графически нуль уравнения: x=sin(x). Предложите один способ приближенного решения этого уравнения. Есть ли нуль уравнения на множестве натуральных чисел? Есть ли нуль уравнения на расширенном множестве натуральных чисел, который получается добавлением нуля к натуральным числам? Указание: постройте графики y=x, y=sin(x).
2. Найти аналитически нуль уравнения: x⁶+27=x⁴-3x²+9 на множестве вещественных чисел. Есть ли нуль уравнения на множестве натуральных чисел? Указание: x⁶+27=(x²)³+3³, x⁴-3x²+9 - разложить на множители, заменив x²=y.
3. Нарисуйте окружность (x—4)²+(y+3)²=16. Найдите его центр и радиус. Запишите уравнение окружности в полярной системе координат. Запишите уравнение концентрической окружности с радиусом равным 2. Указание: заменить x, y по формулам , .

4. Нарисуйте эллипс

   

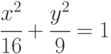
   Найдите его фокальные радиусы, полуоси, эксцентриситет. Запишите уравнение в полярной системе координат. Указание: заменить x, y по формулам , .

5. Нарисуйте гиперболу

   

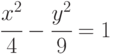
   Найдите его фокусы, полуоси. Запишите уравнение гиперболы в полярной системе координат. Указание: заменить x, y по формулам , .
6. Нарисуйте следующие графики двух парабол на одном рисунке: y=4x², x=8y². Запишите уравнения парабол, симметричных каждой относительно осей координат и нарисуйте их. Указание: оси симметрии парабол – перпендикулярны.
7. Нарисовать сферу (x—1)²+(y—3)²+(z+2)²=9. Укажите ее центр и радиус. Записать уравнение линии, получаемой при пересечении этой сферы и плоскости xOy. Указание: записать уравнение сферы в сферической системе координат.

8. Пересекаются ли две сферы:

   

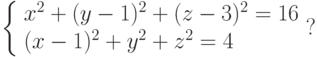
   Найти их точки пересечения, если они пересекаются. Указание: решить систему.

9. Найдите точки пересечения линий:

   

   Нарисуйте это пересечение. Указание: сложить уравнения.
10. Даны вектора 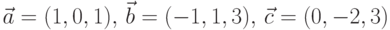. Построить вектор 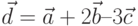, записать его в координатной форме. Найти попарно различные скалярные произведения векторов 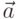, , 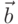, 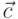проекцию вектора 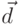на вектор 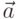, угол между векторами 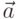, , 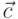уравнение прямой проходящей через начало координат параллельно вектору 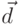, условие параллельности вектора 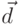вектору , где с – некоторый числовой параметр (найти его). Указание: осуществить прииск по координатными сложением и вычитанием; условие коллинеарности двух векторов – пропорциональность их соответствующих координат.

Темы научных исследований и рефератов (Интернет-листов)

1. Уравнения, их происхождение, изучение и использование в истории древних веков.
2. Неравенства, их происхождение, изучение и использование в истории древних веков.
3. Эволюция уравнений и методов их решения.
4. Эволюция неравенств и методов их решений.
5. Изучение и использование решений уравнений и неравенств в современном мире.
6. Кривые второго порядка и их виды, приложения. Примеры наиболее известных кривых.
7. Поверхности второго порядка и их виды, приложения. Примеры наиболее известных поверхностей.
8. Виды и ориентация прямых на плоскости и в пространстве.
9. Виды и ориентация прямой и плоскости в пространстве и относительно друг друга.
10. Уравнения, неравенства, их приложения в социально-гуманитарных областях.