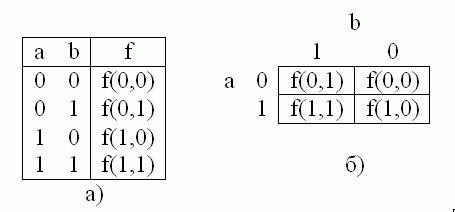Минимизация логических схем
Составление логических выражений по таблице истинности
Каноническая сумма минтермов
Минтерм - это полное произведение всех входных переменных, соответствующее одной строке таблицы истинности, в которой значение выходной переменной (значение функции) равно логической 1. Переменная входит в минтерм с инверсией, если ее значение в данной строке таблицы равно 0, и без инверсии, если ее значение в данной строке таблицы равно 1.
Каноническая сумма минтермов - это логическая сумма всех минтермов, которая представляет собой максимальное логическое выражение, соответствующее таблице истинности.Она составляется в следующей последовательности:
- В заданной таблице истинности подсчитывается
 - количество строк таблицы, в которой значение функции равно 1.
- количество строк таблицы, в которой значение функции равно 1. - Затем записывается логическая сумма
 полных произведений.
полных произведений. - Далее в каждом произведении расставляются инверсии над переменными в соответствии с их значением в строке таблицы.
Для примера, представленного на рис. 1.6, каноническая сумма минтермов будет выглядеть так:
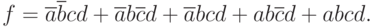 |
( 2.1) |
Из сравнения (1.1) и (2.1) видно, что одной и той же таблице истинности (рис. 1.6,б) соответствуют два разных логических выражения, причем (1.1) записывается более компактно, но возможности минимизации для него еще есть. Следовательно, есть возможность минимизировать и логическую схему, представленную на рис. 1.6, a.
Минимизация логических выражений может осуществляться с помощью различных методов на основе правил булевой алгебры, в частности, диаграммы Вейча, диаграммы Венна и табличным методом, но наиболее простым и наглядным является графический способ минимизации с помощью карт Карно, опубликованный в 1953 г. Морисом Карно.
Минимизация с помощью карт Карно
Карта Карно - графическое представление таблицы истинности. Каждой клетке карты Карно соответствует строка таблицы истинности. По осям карты расставляются сочетания переменных, а внутри карты - значения функции.
Назначение карты Карно - найти логические суммы прямого и инверсного значения переменных. Для любой переменной, например,  , такая сумма равна
, такая сумма равна 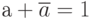 при любом значении
при любом значении  : при
: при 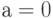 это будет
это будет 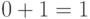 , при
, при 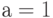 это
это 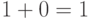 . Поэтому при вынесении за скобки в выражении:
. Поэтому при вынесении за скобки в выражении:
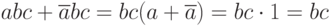
- сумму 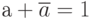 можно отбросить, при этом результат выражения не изменится. В этом и заключается минимизация логических выражений с помощью карт Карно. Для достижения поставленной цели минимизации нужно соблюдать правила разметки осей карты:
можно отбросить, при этом результат выражения не изменится. В этом и заключается минимизация логических выражений с помощью карт Карно. Для достижения поставленной цели минимизации нужно соблюдать правила разметки осей карты:
- Вертикальная ось размечается независимо от горизонтальной.
- Начинать разметку можно с любого сочетания переменных.
- Все сочетания переменных должны быть перечислены.
- Для соседних клеток карты сочетание переменных должно отличаться не более чем одним знаком, причем соседними являются крайние клетки строки (столбца).
Для функции двух переменных карта Карно - это квадрат 2x2 клетки. В этих клетках размещаются 4 значения функции из последнего столбца таблицы истинности (рис. 2.2).
Для функции трех переменных карта Карно - это прямоугольник 2x4 или 4x2 клетки. В этих клетках размещаются 8 значений функции из последнего столбца таблицы истинности (рис. 2.3). При разметке большей из осей нужно четко придерживаться последнего, четвертого правила разметки и следить за тем, чтобы соседними не оказались сочетания  и
и  , либо
, либо 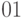 и
и  , в которых одновременно меняются обе переменные.
, в которых одновременно меняются обе переменные.
Для функции четырех переменных карта Карно - это квадрат 4x4 клетки. В этих клетках размещаются 16 значений функции из последнего столбца таблицы истинности (рис. 2.4). При разметке обеих осей нужно также четко придерживаться последнего, четвертого правила разметки и следить за тем, чтобы по одной оси соседними не оказались сочетания  и
и  , либо
, либо 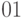 и
и  , в которых одновременно меняются обе переменные.
, в которых одновременно меняются обе переменные.
Для функции пяти переменных карта Карно представляет собой уже объемную фигуру - куб 4x4x4 клетки, поэтому для минимизации логических выражений она не применяется.
увеличить изображение
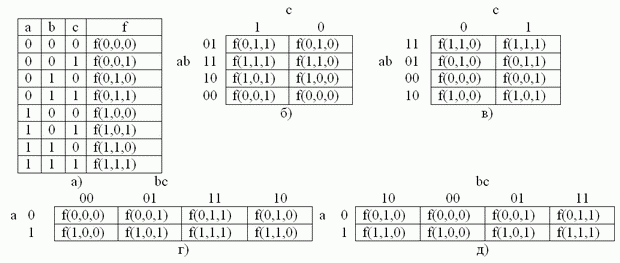
Рис. 2.3. Таблица истинности (а) и примеры заполнения карты Карно (б, в, г, д) для логической функции 3 переменных.
увеличить изображение
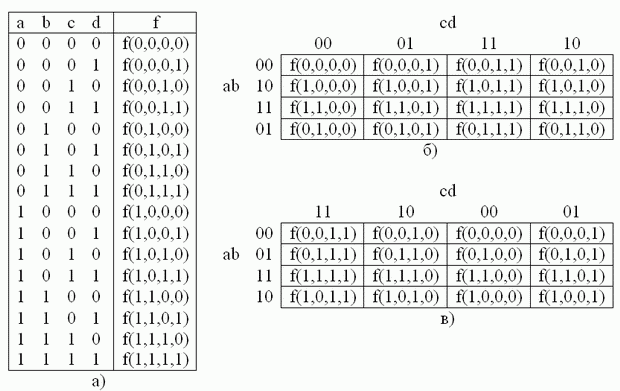
Рис. 2.4. Таблица истинности (а) и примеры заполнения карты Карно (б, в) для логической функции 4 переменных.
В конкретных случаях вместо значений функций в общем виде в клетки карты проставляются конкретные значения (логические 0 и 1) из соответствующих строк таблицы истинности. Затем рассматриваются только те клетки, которые заполнены единицами. Все эти единицы должны быть обведены контурами по следующим правилам составления контуров:
- Контуры должны быть прямоугольными и содержать количество единиц, равное
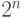 , где
, где  - целое число. Таким образом, в контуре может быть либо одна, либо две, либо четыре, либо восемь единиц.
- целое число. Таким образом, в контуре может быть либо одна, либо две, либо четыре, либо восемь единиц. - Количество единиц в контуре должно быть максимальным, при этом контуры могут пересекаться между собой. Нужно учитывать, что крайние строки являются соседними и крайние столбцы также являются соседними, поэтому контуры могут быть "разорванными".
- Количество контуров должно быть минимальным, но все единицы должны быть охвачены контурами. Нельзя забывать об отдельно стоящих единицах. Каждая такая единица - это контур, которому соответствует полное логическое произведение всех переменных.
После обведения контуров нужно записать минимальное выражение как логическую сумму логических произведений. Каждому произведению соответствует один контур карты Карно. В произведение входят только те переменные, которые остаются в данном контуре неизменными.При этом переменная входит в произведение с инверсией, если ее значение в данном контуре равно 0, и без инверсии, если ее значение равно 1.
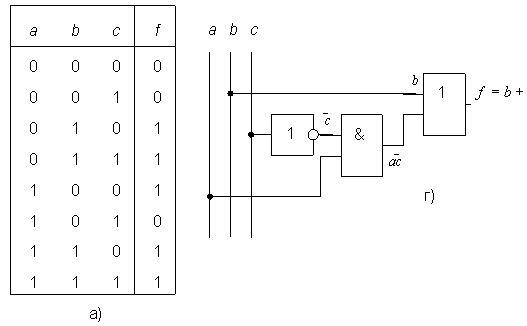
Пример 1. Написать минимальное выражение для таблицы истинности, представленной на рис. 2.5,а и нарисовать по нему логическую схему.
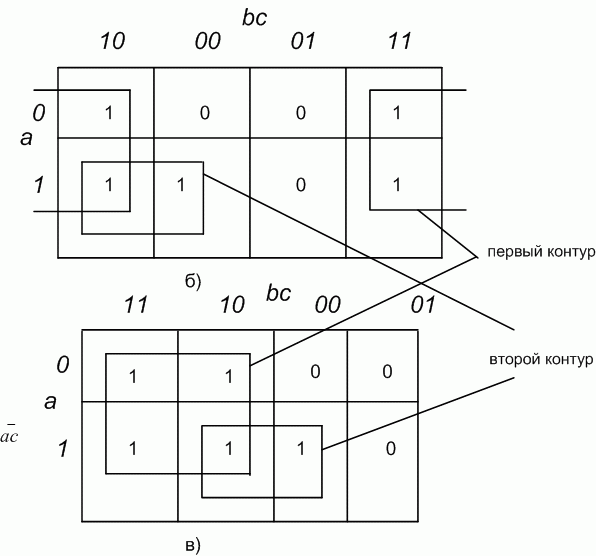
При одном варианте разметки осей (рис. 2.5,б) первый контур, состоящий из четырех единиц, получается разорванным. Если же принять разметку, показанную на рис. 2.5,в, то контур будет иметь нормальные очертания, а выражение, ему соответствующее, останется без изменений. Учитывая, что при данном горизонтальном начертании карты Карно крайние столбцы являются соседними, ее можно представить себе как цилиндр, развернутый на плоскости. На рис. 2.5,б представлена развертка такого цилиндра, "разрезанная" между комбинациями 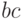 , равными
, равными  и
и  . А на рис. 2.5,в представлена развертка этого же цилиндра, "разрезанная" между произведениями
. А на рис. 2.5,в представлена развертка этого же цилиндра, "разрезанная" между произведениями 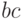 , равными
, равными  и
и 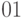 .
.
Первый контур охватывает четыре единицы, ему соответствует сумма минтермов:  ,
в которой не изменяется только переменная
,
в которой не изменяется только переменная  . Второй контур охватывает две единицы. Ему соответствует сумма минтермов
. Второй контур охватывает две единицы. Ему соответствует сумма минтермов  , в которой переменная
, в которой переменная  принимает оба возможных значения, а произведение
принимает оба возможных значения, а произведение 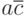 остается неизменным. Таким образом, получаем минимальное выражение:
остается неизменным. Таким образом, получаем минимальное выражение:
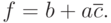 |
( 2.2) |
Ему соответствует логическая схема на рис. 2.5,г.
Для сравнения запишем максимальное выражение:
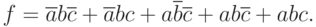 |
( 2.3) |
Разница между (2.2) и (2.3) очевидна и в комментариях не нуждается, за исключением того, что схема, реализованная по (2.3), будет на порядок сложнее и, соответственно, менее надежна, чем схема, показанная на рис. 2.5,г.
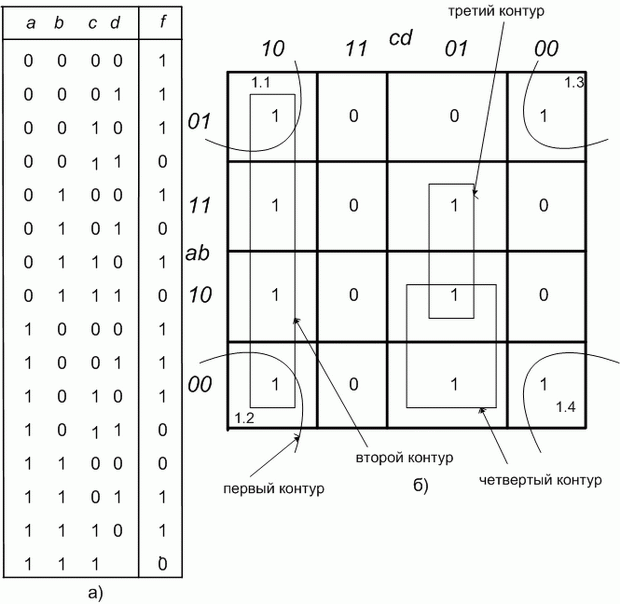
Пример 2. Написать минимальное выражение для таблицы истинности, представленной на рис. 2.6,а, и нарисовать по нему логическую схему.
При первоначально выбранной разметке осей (рис. 2.6,б) первый контур, состоящий из четырех единиц с номерами 1.1, 1.2, 1.3 и 1.4, расположенных по углам карты, получается разорванным. Если же принять разметку, показанную на рис. 2.7, то контур будет иметь очертания квадрата, а выражение, ему соответствующее, останется без изменений. Учитывая, что крайние столбцы являются соседними и крайние строки являются соседними, карту Карно для функции четырех переменных можно представить себе как торроид, развернутый на плоскости. Проще представить себе обратный процесс получения торроида из плоской фигуры - квадрата. Для этого надо сначала соединить мысленно крайние строки - получим цилиндр. После этого основания цилиндров надо мысленно соединить. Получится торроид. На рис. 2.6,б представлена развертка такого торроида, "разрезанная" между комбинациями 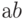 , равными
, равными 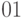 и
и  и между сочетаниями
и между сочетаниями 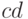 , равными
, равными  и
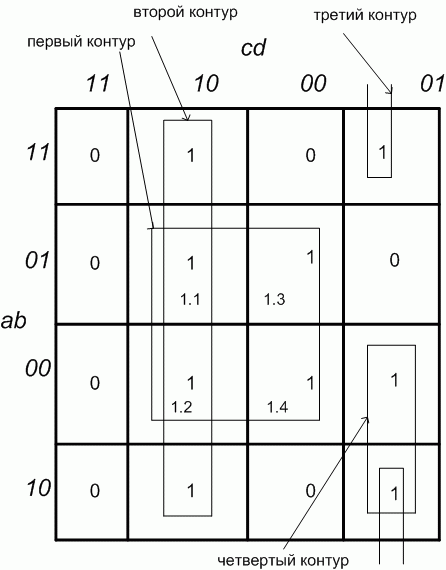
и  . А на рис. 2.7 представлена развертка этого же торроида, "разрезанная" между комбинациями
. А на рис. 2.7 представлена развертка этого же торроида, "разрезанная" между комбинациями 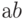 , равными
, равными  и
и  и между произведениями
и между произведениями 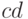 , равными
, равными  и
и 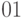 . После анализа контуров получим минимальное выражение
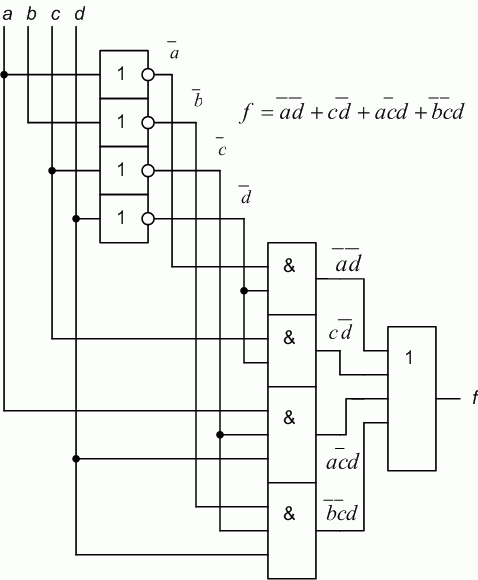
. После анализа контуров получим минимальное выражение 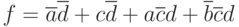 . Соответствующая ему схема приведена на рис. 2.8.
. Соответствующая ему схема приведена на рис. 2.8.