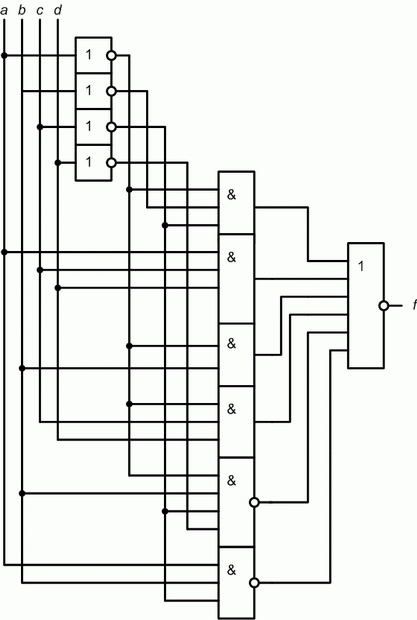
Минимизация логических схем
Ключевые термины
ДНФ - дизъюнктивно-нормальная форма - представление логического выражения в виде произведения сумм.
Каноническая сумма минтермов - это логическая сумма всех минтермов, которая представляет собой максимальное логическое выражение, соответствующее таблице истинности.
Каноническое произведение макстермов - это логическое произведение всех макстермов, которая представляет собой максимальное логическое выражение, соответствующее таблице истинности.
Карта Карно - графическое представление таблицы истинности.
КНФ - конъюнктивно-нормальная форма - представление логического выражения в виде суммы произведений.
Макстерм - это сумма всех входных переменных, соответствующее одной строке таблицы истинности, в которой значение выходной переменной (значение функции) равно 0. Переменная входит в макстерм с инверсией, если её значение в строке истинности равно 1.
Минтерм - это полное произведение всех входных переменных, соответствующее одной строке таблицы истинности, в которой значение выходной переменной (значение функции) равно логической 1. Переменная входит в минтерм с инверсией, если её значение в строке истинности равно 0.
Краткие итоги
Работа логической схемы наиболее наглядно может быть описана с помощью таблицы истинности. Возможно и решение обратной задачи - по известной таблице истинности синтезировать логическое выражение и логическую схему. Для синтеза схем применяется метод минимизации с помощью карт Карно. Наиболее рациональная логическая схема может быть синтезирована по минимизированному логическому выражению.
Набор для практики
Вопросы для самопроверки
- Каково правило логического сложения? умножения?
- Какой сигнал является решающим для логического сложения? умножения?
- Что такое минтерм?
- Что такое таблица истинности?
- Сколько строк в таблице истинности для 7-входовой логической схемы?
- Что означает аббревиатура ДНФ? КНФ?
- Объясните соответствие карты Карно и таблицы истинности.
- Для какого максимального количества переменных практически применимы карты Карно?
- Почему при размётке осей карты Карно сочетания
 и
и  не могут быть соседними?
не могут быть соседними? - На чём основан принцип минимизации логических выражений?
- Какое количество единиц может содержать один контур в карте Карно для функции двух переменных? Трёх? Четырёх? Пяти?
- Допустимо ли пересечение контуров на карте Карно?
Упражнения к лекциям 1 и 2
Примеры решения подобных задач подробно рассматриваются в [2].
Упражнение 1.
Вариант 1 упражнения 1. Написать каноническую сумму минтермов и нарисовать минимальную логическую схему для логического выражения
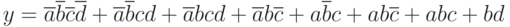
Вариант 2 упражнения 1. Написать каноническую сумму минтермов и нарисовать минимальную логическую схему для логического выражения
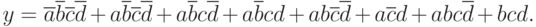
Вариант 3 упражнения 1. Написать каноническую сумму минтермов и нарисовать минимальную логическую схему для логического выражения
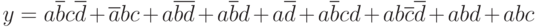
Вариант 4 упражнения 1. Написать каноническую сумму минтермов и нарисовать минимальную логическую схему для логического выражения
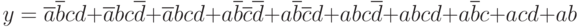
Вариант 5 упражнения 1. Написать каноническую сумму минтермов и нарисовать минимальную логическую схему для логического выражения
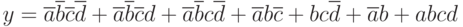
Вариант 6 упражнения 1. Написать каноническую сумму минтермов и нарисовать минимальную логическую схему для логического выражения

Вариант 7 упражнения 1. Написать каноническую сумму минтермов и нарисовать минимальную логическую схему для логического выражения
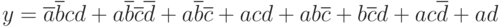
Вариант 8 упражнения 1. Написать каноническую сумму минтермов и нарисовать минимальную логическую схему для логического выражения
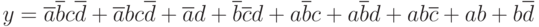
Вариант 9 упражнения 1. Написать каноническую сумму минтермов и нарисовать минимальную логическую схему для логического выражения

Вариант 10 упражнения 1. Написать каноническую сумму минтермов и нарисовать минимальную логическую схему для логического выражения
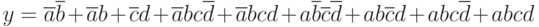
Упражнение 2.
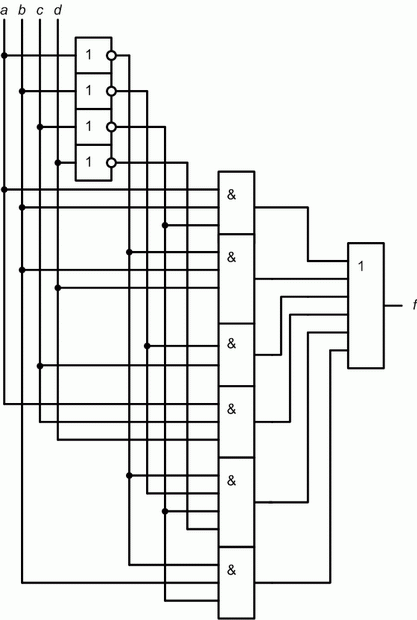
Вариант 1 упражнения 2. Минимизировать логическую схему
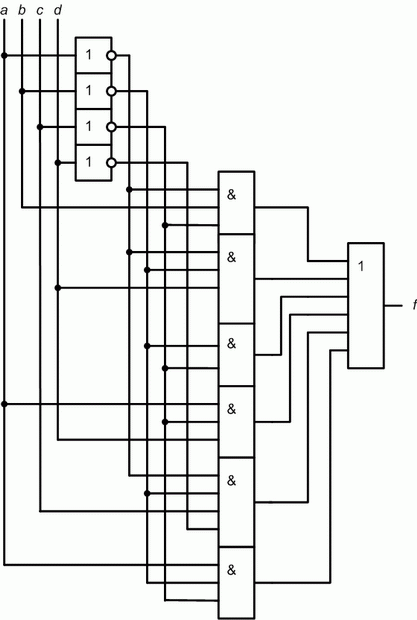
Вариант 2 упражнения 2. Минимизировать логическую схему
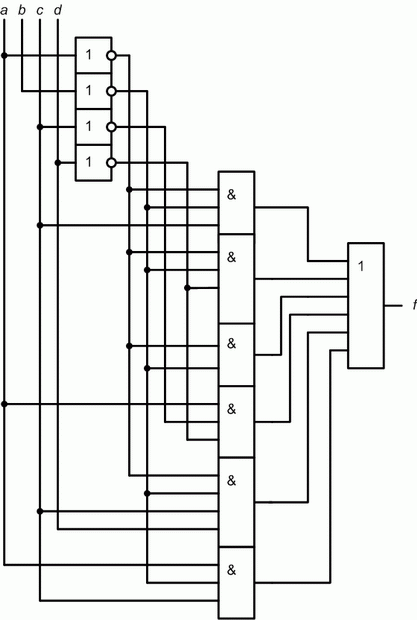
Вариант 3 упражнения 2. Минимизировать логическую схему
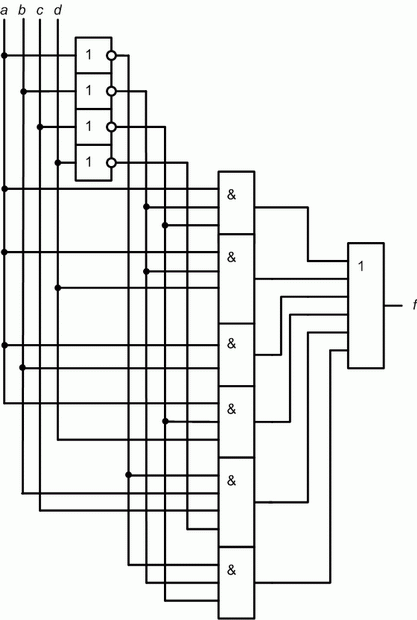
Вариант 4 упражнения 2. Минимизировать логическую схему
Вариант 5 упражнения 2. Минимизировать логическую схему
Вариант 6 упражнения 2. Минимизировать логическую схему
Вариант 7 упражнения 2. Минимизировать логическую схему
Вариант 8 упражнения 2. Минимизировать логическую схему
Вариант 9 упражнения 2. Минимизировать логическую схему
Вариант 10 упражнения 2. Минимизировать логическую схему