Счетные схемы ЭВМ. Счетчики и сумматоры
Счетными схемами, лежащими в основе построения арифметических устройств ЭВМ, являются счетчики и сумматоры. Любые, даже самые сложные, вычислительные схемы представляют собой комбинацию счетчиков различных разновидностей и сумматоров, реализующих вычисления, как правило, в дополнительном коде (подробно кодирование информации в двоичном коде и соответствующая арифметика представлены в "Заключение" ).
Двоичные счетчики
Счетчиком называют функциональный узел, предназначенный для счета сигналов [1, c. 252].
По мере поступления входных сигналов счетчик последовательно перебирает свои состояния в определенном для данной схемы порядке. В частности, двоичные счетчики, рассматриваемые в настоящем пособии, перебирают последовательность двоичных кодов. В том случае, если последовательность выдается с возрастанием кода, счетчик называется суммирующим, если код уменьшается с приходом каждого счетного сигнала, то счетчик называется вычитающим. Если в счетчике предусмотрено переключение из суммирующего режима в вычитающий и обратно, он называется реверсивным. Количество схем счетчиков огромно [1, 2, 3]. Их изучение является отдельной, обширной темой, и задачей данного курса не является.
Простейший синхронный суммирующий счетчик можно построить на счетных, или Т -триггерах (от англ . toggle - кувыркаться). Счетным Т -триггером называют так называемый JK -триггер, который работает в счетном режиме, когда на J- и K -входы постоянно подана логическая 1. JK -триггер представляет собой соединение двух однотактных D -триггеров-защелок (рис. 9.1.а), на С -входы которых поступают противоположные уровни сигналов.
При подаче 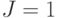 и
и 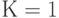 на выходе нижнего элемента И будет постоянный логический 0, поскольку
на выходе нижнего элемента И будет постоянный логический 0, поскольку 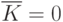 . А состояние верхнего элемента И будет определяться состоянием выхода
. А состояние верхнего элемента И будет определяться состоянием выхода  всей схемы. Если в предыдущий момент времени
всей схемы. Если в предыдущий момент времени 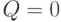 , а
, а 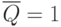 то на выходе элемента И-ИЛИ будет логическая
то на выходе элемента И-ИЛИ будет логическая  . При
. При 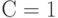 она записывается в первый D -триггер, а при отрицательном фронте на
она записывается в первый D -триггер, а при отрицательном фронте на 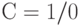 - во второй D -триггер и выдается на выход
- во второй D -триггер и выдается на выход  всей схемы: формируется передний фронт импульса
всей схемы: формируется передний фронт импульса 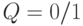 . При
. При 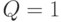 на инверсном выходе схемы
на инверсном выходе схемы 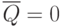 . Этот сигнал переведет при
. Этот сигнал переведет при 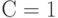 первый D
-триггер в нулевое состояние, а при
первый D
-триггер в нулевое состояние, а при 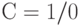 - второй D -триггер и выход
- второй D -триггер и выход  всей схемы переводится в нулевое состояние схемы (формируется задний фронт импульса
всей схемы переводится в нулевое состояние схемы (формируется задний фронт импульса 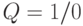 ) так, как показано на рис. 9.1,б.
) так, как показано на рис. 9.1,б.
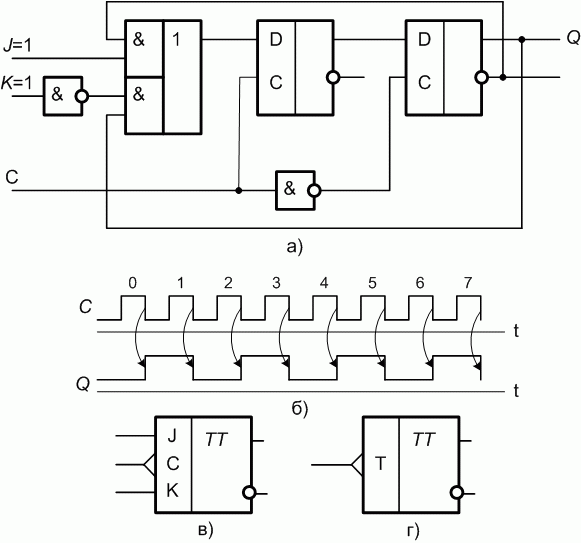
Рис. 9.1. JK-триггер: а - функциональная схема; б - временная диаграмма работы; в - УГО JK-триггера; г - УГО счетного Т-триггера
Таким образом, в счетном режиме частота входных сигналов уменьшается в два раза. Факт переключения триггера в противоположное состояние при прохождении заднего фронта сигнала  отображается на УГО динамическим входом в виде треугольника (рис. 9.1,в и г). Все ранее рассмотренные управляющие сигналы были статическими.
отображается на УГО динамическим входом в виде треугольника (рис. 9.1,в и г). Все ранее рассмотренные управляющие сигналы были статическими.
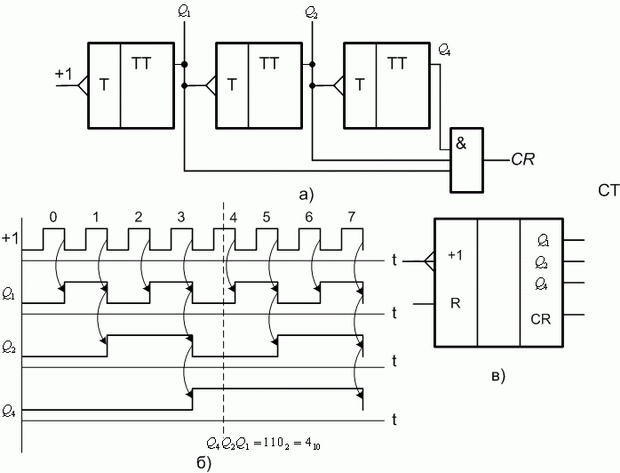
При последовательном соединении нескольких счетных Т-триггеров получаем схему простейшего синхронного счетчика (рис. 9.2,а). При этом выход самого последнего триггера будет являться самым старшим разрядом двоичного кода на выходе счетчика, выход самого первого триггера - младшим разрядом в соответствии с временной диаграммой, представленной на рис. 66,б. Данной схеме соответствует УГО на рис. 9.2.б. Как правило, у счетчиков предусматриваются вход  для принудительного сброса в нулевое состояние (когда все триггеры схемы сброшены в
для принудительного сброса в нулевое состояние (когда все триггеры схемы сброшены в  ) и выход переноса
) и выход переноса  , устанавливаемый в 1 в том случае, когда прошла вся последовательность импульсов (рис. 9.2,в). Для схемы 3-разрядного счетчика, представленной на рис. 9.2, это коды от 000_{2} до 111_{2}.
, устанавливаемый в 1 в том случае, когда прошла вся последовательность импульсов (рис. 9.2,в). Для схемы 3-разрядного счетчика, представленной на рис. 9.2, это коды от 000_{2} до 111_{2}.
увеличить изображение
Рис. 9.2. Суммирующий двоичный счетчик: а - функциональная схема; б - временная диаграмма работы; в - УГО
Выход переноса может быть использован для последовательного соединения нескольких счетчиков с целью повышения разрядности подсчитываемого числа. Такие схемы называются схемами с последовательным переносом. Существуют также и более сложные схемы с параллельным переносом [1, c. 257-262].
Сумматоры
Сумматором называют функциональный узел, выполняющий сложение одно- или многоразрядных двоичных чисел в соответствии с правилами двоичного сложения.
Подробно вопросы двоичной арифметики освещены в "Заключение" . Правила двоичного сложения можно представить в виде таблицы истинности будущей логической схемы (табл. 9.1) двоичного сумматора и построить эту схему по принципам, изложенным в лекции 3.
Входной перенос из младшего по (отношению к текущему) разряда 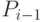 |
Текущий разряд первого слагаемого  |
Текущий разряд второго слагаемого  |
Текущий разряд суммы 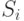 |
Выходной перенос из текущего разряда суммы 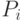 |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Для текущего разряда суммы 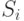 логическое выражение имеет вид:
логическое выражение имеет вид:

причем согласно карте Карно, представленной на рис. 9.3,а, данное выражение не минимизируется. Для выходного переноса 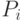 минимизация возможна, поэтому логическое выражение согласно рис. 9.3,б, получается следующим:
минимизация возможна, поэтому логическое выражение согласно рис. 9.3,б, получается следующим:
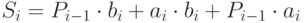
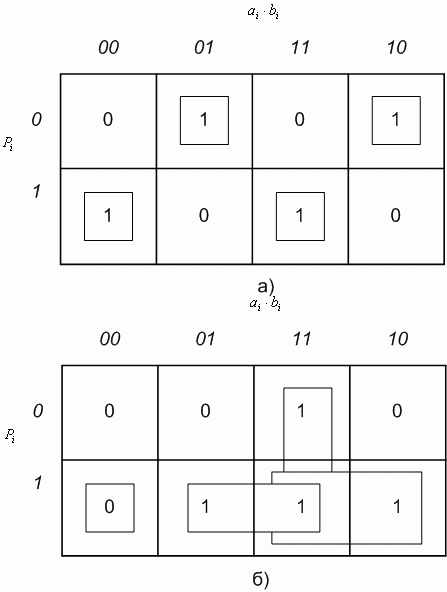
Рис. 9.3. Карты Карно для одноразрядного сумматора: а - для текущего разряда суммы; б - для текущего разряда выходного переноса
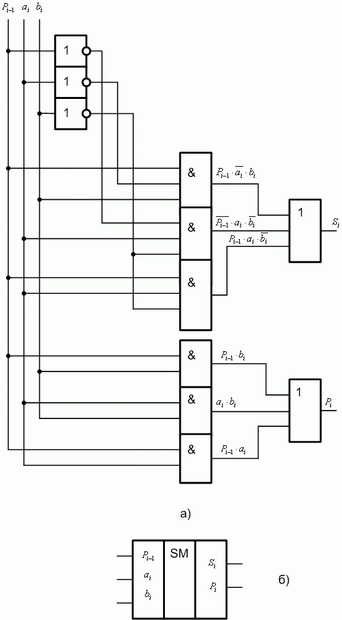
Схема одноразрядного сумматора и его УГО представлены на рис. 9.4.