Логические основы ЭВМ
Любая цифровая вычислительная машина состоит из логических схем - таких схем, которые могут находиться только в одном из двух возможных состояний - либо "логический ноль", либо "логическая единица". За логический 0 и логическую 1 можно принять любое выражение, в том числе и словесное, которое можно характеризовать как "истина" и "ложь". В вычислительной технике логические 0 и 1 - это состояние электрических схем с определенными параметрами. Так, для логических элементов и схем, выполненных по технологии транзисторно-транзисторной логики (ТТЛ-схемы), логический 0 - это напряжение в диапазоне 0 … + 0,4 В, а логическая 1 - это напряжение в диапазоне + 2,4 … + 5 В [1]. Работа логических схем описывается посредством специального математического аппарата, который называется логической (булевой) алгеброй или алгеброй логики. Булева алгебра была разработана Джорджем Булем (1815 - 1864 гг.), она является основой всех методов упрощения булевых выражений.
Логические переменные и логические функции - это такие переменные и функции, которые могут принимать только два значения - либо логический 0, либо логическая 1.
Основные логические функции и элементы
Логический элемент - графическое представление элементарной логической функции.
Логическое умножение (конъюнкция) - функция И
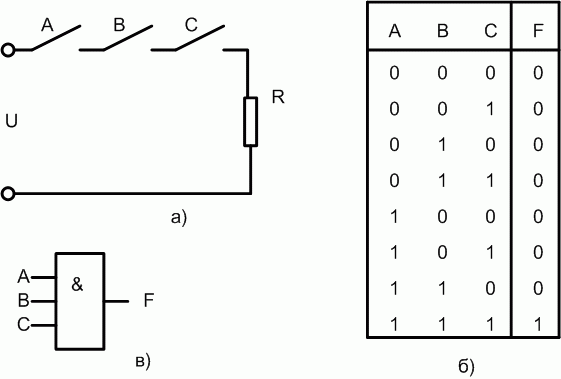
Рассмотрим ключевую схему представленную на рис. 1.1,а. Примем за логический 0 [2]:
- на входе схемы разомкнутое состояние соответствующего ключа, например,
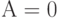 ;
; - на выходе схемы (
 ) - такое ее состояние, когда через сопротивление R ток не протекает.
) - такое ее состояние, когда через сопротивление R ток не протекает.
Таблица истинности - это таблица, содержащая все возможные комбинации входных логических переменных и соответствующие им значения логической функции.
Таблица истинности для логической схемы, представленной на рис. 1.1,б, состоит из 8 строк, поскольку данная схема имеет три входа -  ,
, 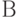 и
и  . Каждая из этих логических переменных может находиться либо в состоянии логического 0, либо логической 1. Соответственно количество сочетаний этих переменных равно
. Каждая из этих логических переменных может находиться либо в состоянии логического 0, либо логической 1. Соответственно количество сочетаний этих переменных равно 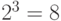 . Очевидно, что через сопротивление R ток протекает только тогда, когда замкнуты все три ключа - и
. Очевидно, что через сопротивление R ток протекает только тогда, когда замкнуты все три ключа - и  , и
, и 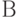 , и
, и  . Отсюда еще одно название логического умножения - логический элемент И. В логических схемах этот элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.1,в.
. Отсюда еще одно название логического умножения - логический элемент И. В логических схемах этот элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.1,в.
Правило логического умножения :если на вход логического элемента И подается хотя бы один логический 0, то на его выходе будет логический 0.
Уровень логического 0 является решающим для логического умножения .
В логических выражениях применяется несколько вариантов обозначения логического умножения. Так, для приведенного на рис. 1.1,в трёх-входового элемента И, логическое выражение можно представить в виде:
- либо
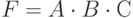 , но при этом из контекста должно быть ясно, что данное умножение именно логическое;
, но при этом из контекста должно быть ясно, что данное умножение именно логическое; - либо
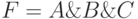 ;
; - либо
 - с использованием знака конъюнкции;
- с использованием знака конъюнкции; - либо
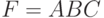 , но при этом из контекста должно быть ясно, что между переменными
, но при этом из контекста должно быть ясно, что между переменными  ,
,  и
и  производится логическое умножение.
производится логическое умножение.
Логическое сложение (дизъюнкция) - функция ИЛИ
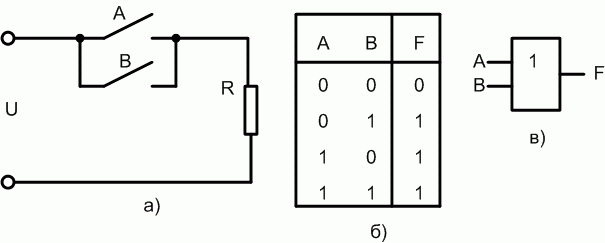
Рассмотрим ключевую схему, представленную на рис. 1.2,а. Таблица истинности для данной логической схемы (рис. 1.2,б) состоит из 4 строк, поскольку данная схема имеет два входа -  и
и 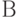 . Количество сочетаний этих переменных равно
. Количество сочетаний этих переменных равно 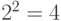 . Очевидно, что через сопротивление R ток протекает тогда, когда замкнуты или
. Очевидно, что через сопротивление R ток протекает тогда, когда замкнуты или  , или
, или 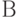 . Отсюда еще одно название логического сложения - логическое ИЛИ. В логических схемах соответствующий логический элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.2,в.
. Отсюда еще одно название логического сложения - логическое ИЛИ. В логических схемах соответствующий логический элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.2,в.
Правило логического сложения: если на вход логического элемента ИЛИ подается хотя бы одна логическая  , то на его выходе будет логическая 1.
, то на его выходе будет логическая 1.
Для логического сложения решающим является уровень логической 1.
В логических выражениях применяется два варианта обозначения логического сложения. Так, для приведенного двух-входового элемента ИЛИ, логическое выражение можно представить в виде:
- либо
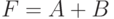 , но при этом из контекста должно быть ясно, что данное сложение именно логическое;
, но при этом из контекста должно быть ясно, что данное сложение именно логическое; - либо
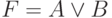 - с использованием знака дизъюнкции.
- с использованием знака дизъюнкции.
Логическое отрицание (инверсия) - функция НЕ
Рассмотрим ключевую схему, представленную на рис. 1.3,а. Таблица истинности для данной схемы (рис. 1.3,б) самая простая и состоит всего из 2 строк, поскольку она (единственная из всех логических элементов) имеет только один вход -  . Количество вариантов для единственной логической переменной равно
. Количество вариантов для единственной логической переменной равно 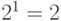 . Очевидно, что через сопротивление R ток протекает (
. Очевидно, что через сопротивление R ток протекает ( 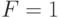 ) тогда, когда
) тогда, когда  не замкнут, т.е.
не замкнут, т.е. 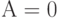 . Еще одно название этой логической функции - отрицание, а соответствующий логический элемент называется инвертором. В логических схемах этот элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.3,в. Поскольку он имеет
только один вход, в его обозначении допустимым является и знак логического сложения, и знак логического умножения.
. Еще одно название этой логической функции - отрицание, а соответствующий логический элемент называется инвертором. В логических схемах этот элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.3,в. Поскольку он имеет
только один вход, в его обозначении допустимым является и знак логического сложения, и знак логического умножения.
Правило инверсии: проходя через инвертор, сигнал меняет свое значение на противоположное.
В логических выражениях применяется единственный вариант обозначения инверсии:

К основным логическим элементам относятся еще два элемента, которые являются комбинацией элементов И, ИЛИ и НЕ: элемент И-НЕ и ИЛИ-НЕ.
Логическая функция и элемент И-НЕ
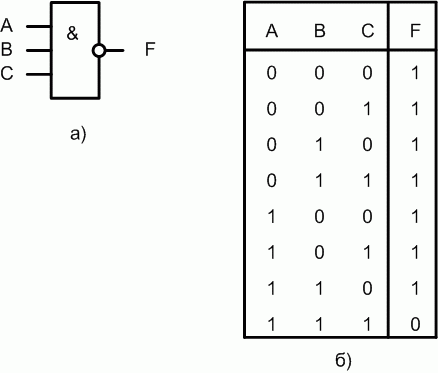
Данная функция производит логическое умножение значений входных сигналов, а затем инвертирует результат этого умножения. В логических схемах этот элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.4,а. Таблица истинности приведена на рис. 1.4,б.
Если на вход логического элемента И-НЕ подается хотя бы один логический 0, то на его выходе будет логическая 1.
В логических выражениях применяются обозначения:
- либо
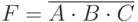 , но при этом из контекста должно быть ясно, что данное умножение именно логическое;
, но при этом из контекста должно быть ясно, что данное умножение именно логическое; - либо
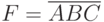 ;
; - либо
 ;
; - либо
 .
.
Логическая функция и элемент ИЛИ-НЕ
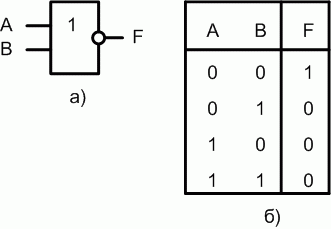
В логических схемах этот элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.5,а. Таблица истинности приведена на рис. 1.5,б.
Если на вход логического элемента ИЛИ-НЕ подается хотя бы одна логическая 1, то на его выходе будет логический 0.В логических выражениях применяются обозначения:
- либо
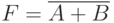 , но при этом из контекста должно быть ясно, что данное сложение именно логическое;
, но при этом из контекста должно быть ясно, что данное сложение именно логическое; - либо
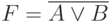 .
.