|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Управление организационно-экономической устойчивостью промышленных корпоративных систем на основе динамического анализа состояния в условиях неопределенности
Внутренние факторы делятся на контролируемые и частично контролируемые. Первые не ведут к возникновению неопределенностей, вторые делятся на технологические и организационные.
Технологические факторы:
- Ухудшение качества продукции (снижает объем продаж, ведет к потерям в объемах продаж
 );
); - Снижение производительности производства, связанного с проектом (ведет к снижению объема продаж, захвату доли рынка конкурентами, выражается в недополучении части выручки в размере
 );
); - Ошибки в проектносметной документации (требуют дополнительных затрат на их устранение
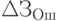 ).
).
Организационные факторы:
- Срывы планов работ из-за:
недостатка рабочей силы (
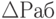 );
нехватки материалов (
);
нехватки материалов (  );
поздней поставки материалов (
);
поздней поставки материалов ( 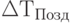 );
изменения возможностей заказчика проекта, подрядчиков (
);
изменения возможностей заказчика проекта, подрядчиков (  );
ошибок проектирования (
);
ошибок проектирования (  );
>ошибок планирования (
);
>ошибок планирования (  );
недостатка координации работ (\Delta О_{Корд});
изменения руководства (
);
недостатка координации работ (\Delta О_{Корд});
изменения руководства (  ).
из-за банкротства подрядчиков (зависят от надежности подрядчиков
).
из-за банкротства подрядчиков (зависят от надежности подрядчиков  и тщательности выбора подрядчиков при заключении котрактов. Ведут к потерям, которые можно оценить по величине дополнительных средств
и тщательности выбора подрядчиков при заключении котрактов. Ведут к потерям, которые можно оценить по величине дополнительных средств  , которые необходимо привлечь для компенсации отставания в графике реализации проекта, выплатить в виде штрафов, неустоек);
из-за задержек в финансировании (зависит от надежности
, которые необходимо привлечь для компенсации отставания в графике реализации проекта, выплатить в виде штрафов, неустоек);
из-за задержек в финансировании (зависит от надежности 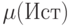 источника в случае внешнего финансирования, тщательности проработки инвестиционного плана
источника в случае внешнего финансирования, тщательности проработки инвестиционного плана  - в случае реинвестирования части прибыли. Выражается в сумме дополнительных затрат для компенсации возможных потерь:
- в случае реинвестирования части прибыли. Выражается в сумме дополнительных затрат для компенсации возможных потерь: 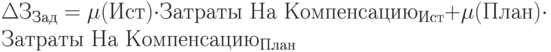 );
); - Перерасход средств из-за:
- срывов планов работ
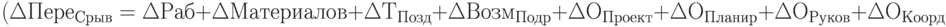
- неправильной стратегии снабжения (
 );
); - неквалифицированного персонала (
 );
); - переплат по материалам, услугам и т. д. (
 );
); - неправильных смет (
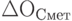 );
); - других неучтенных факторов.
- срывов планов работ
Страхуемые факторы:
- Прямой ущерб имуществу:
- транспортные инциденты (
 );
); - оборудование (
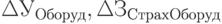 );
); - материалы (
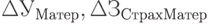 ).
).
- транспортные инциденты (
- Косвенные потери:
- демонтаж и передислокация поврежденного имущества (
 );
); - перестановка оборудования (
 );
); - потери арендной прибыли (
 );
); - нарушение запланированного ритма деятельности (
 ).
).
- демонтаж и передислокация поврежденного имущества (
- Страхуемые в соответствии с нормативными документами посторонним лицам
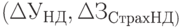 .
. - Страхование сотрудников:
- телесные повреждения (
 );
); - затраты на замену сотрудников (
 );
); - потери прибыли (
 ).
).
- телесные повреждения (
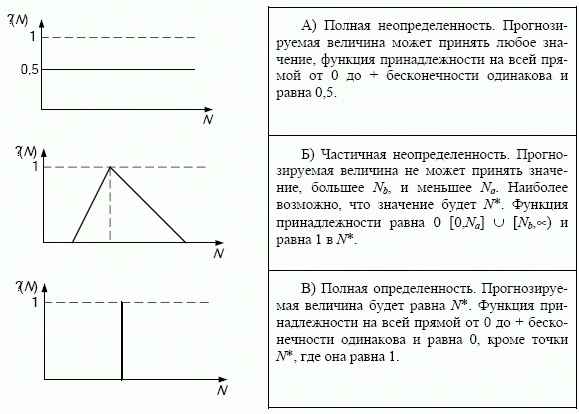
Ясно, что наличие такого количества неопределенных факторов при прогнозировании (см. также [18, 17]) делает невозможным определить точный график изменения прогнозируемой величины, т. к. на нее обычно влияет очень много различных факторов, информация о которых не всегда полностью известна. В результате вектора состояния подсистем ВПС в будущем могут быть известны только в виде нечеткого множества (рис. 8.18). Иначе говоря, точность прогноза зависит от того, известна ли вся информация о тех системах, которые влияют на прогнозируемую.
Все перечисленные выше факторы не могут быть заранее известны с достаточной степенью точности [18, 17].
Суждения о том, насколько возможно проявление того или иного фактора, могут лишь сузить область полной неопределенности (при котором все состояния имеют одинаковую степень возможности, или в терминах нечетких множеств, одинаковые значения функции принадлежности) до нечеткого множества [21].
Иллюстрация зависимости точности прогноза от степени информированности эксперта представлена на рис. 8.18.
На практике наиболее часто встречается случай Б, т. к. на прогнозируемую величину влияет много различных параметров и полную информацию о всех параметрах получить и обработать физически невозможно.
Действительно, при определении, например, возможных объемов сбыта производимой предприятием продукции можно лишь оценить объем в прогнозируемый период времени следующей величиной:
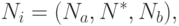
где 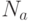 - нижняя граница оценки объема сбыта;
- нижняя граница оценки объема сбыта; 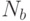 - верхняя граница оценки объема сбыта;
- верхняя граница оценки объема сбыта; 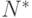 - наиболее возможный объем сбыта.
- наиболее возможный объем сбыта.
Аналогично, при прогнозировании других параметров, входящих в целевую функцию, можно получить следующие оценки: цена - 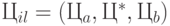 , расход материала -
, расход материала - 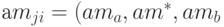 ) выплаты в государственные органы -
) выплаты в государственные органы -  , и т. д.
, и т. д.
Следовательно, прогнозы изменения векторов состояния подсистем могут быть записаны в следующем виде:
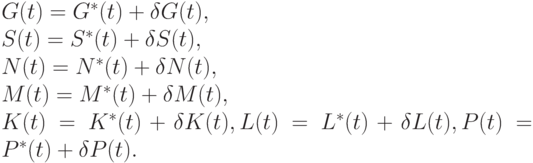
А так как результат деятельности предприятия зависит от векторов состояния всех подсистем ВПС, то он тоже будет неопределенным:

Все перечисленные выше факторы, вносящие неопределенность в работу предприятия, должны быть учтены при прогнозировании. Для этого необходимо разработать методики учета неопределенности и выбрать наилучшую из них для построения экономико-математической модели функционирования предприятия.
Следовательно, существует проблема, выражающаяся в нечеткости входных информационных потоков на предприятиях. Это ведет к погрешностям при прогнозировании, что оказывает влияние на точность моделирования положения предприятия и сказывается на эффективности функционирования системы управления. Все это ведет к снижению устойчивости предприятия.
Выбор методики учета неопределенности. Для преодоления проблемы наличия неопределенности необходимо выбрать методику ее учета при анализе информационных потоков. На основании выбранной методики можно будет разработать метод прогнозирования, учитывающий неопределенность. На базе метода разрабатывается модель, составляющая основу системы управления предприятием.
Для обработки неопределенностей можно предложить два подхода:
- устранение нечеткости информации;
- построение модели, оперирующей нечеткими исходными данными.
Рассмотрим обе методики.
Первый подход назовем методом устранения нечеткости. Для устранения нечеткости входной информации предлагается уменьшить погрешности преобразования информации перед вводом в модель. Внешние и внутренние характеристики информационного потока при этом не должны измениться больше, чем на величину, сопоставимую с погрешностью модели предприятия:
 |
( 8.22) |
где  - погрешность преобразования информации до ввода в модель;
- погрешность преобразования информации до ввода в модель;  - погрешность (точность) модели. Погрешности вычисляются по следующим формулам:
- погрешность (точность) модели. Погрешности вычисляются по следующим формулам:
 |
( 8.23) |
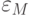 - обычно задается в модели при вычислениях. где
- обычно задается в модели при вычислениях. где  - интегральная характеристика [7] информационного потока,
- интегральная характеристика [7] информационного потока,
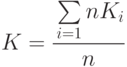
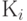 - коэффициент, отражающий
- коэффициент, отражающий  -ю характеристику потока, индекс "до" относится к состоянию информации до ее преобразования; индекс "после" - соответственно характеристика после преобразования.
-ю характеристику потока, индекс "до" относится к состоянию информации до ее преобразования; индекс "после" - соответственно характеристика после преобразования.
Этот принцип можно назвать "расширение узких мест".
Для уменьшения погрешностей при обработке информации необходимо исследовать причины возникновения этой погрешности. Из представленной классификации видно, что свойства информации однозначно определяются тем, как информация собиралась, транспортировалась и обрабатывалась.
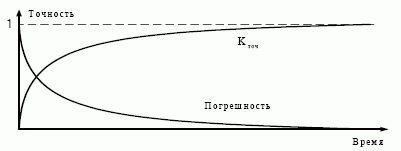
Точность информации зависит от времени, затраченного на ее сбор. Видно, что чем дольше собирают исходные данные, тем более точно отражают они действительность, т. е. погрешность информации уменьшается. Вместе с тем чем меньше информации остается собрать, тем труднее идет процесс сбора, и сильно увеличиваются издержки (рис. 8.19).
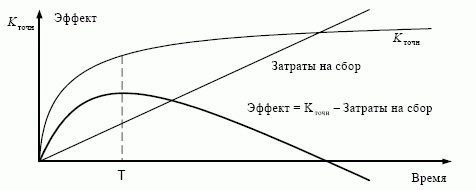
В момент времени 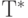 становится невыгодно дальнейшее увеличение точности, т. к. издержки растут быстрее, чем выгода от уменьшения неопределенности. Следовательно, возникает противоречие - с одной стороны, для эффективного управления необходимо увеличение точности, с другой стороны - это приводит к увеличению затрат и уменьшению оперативности системы управления. Следовательно, данный подход к увеличению эффективности управления предприятием является неприемлемым (рис. 8.20).
становится невыгодно дальнейшее увеличение точности, т. к. издержки растут быстрее, чем выгода от уменьшения неопределенности. Следовательно, возникает противоречие - с одной стороны, для эффективного управления необходимо увеличение точности, с другой стороны - это приводит к увеличению затрат и уменьшению оперативности системы управления. Следовательно, данный подход к увеличению эффективности управления предприятием является неприемлемым (рис. 8.20).
Рассмотрим второй подход к учету неопределенности информационных потоков. Назовем его обработкой нечеткостей в том виде, в каком они поступили на вход модели. Для этого необходимо создать модель, которая может работать с информацией, поступившей на вход, в ее естественном виде (т. е. с учетом ее нечеткости). При этом автоматически
исчезают погрешности  которые возникали в предыдущем методе. Равенство нулю
погрешностей связано с отсутствием самих процессов преобразований.
которые возникали в предыдущем методе. Равенство нулю
погрешностей связано с отсутствием самих процессов преобразований.
Как мы выяснили выше, нецелесообразно увеличивать Кточн больше некоего определенного значения  (ср. [18, 19]). Это означает, что информация, поступающая на вход модели, останется в некоторой степени неопределенной.
(ср. [18, 19]). Это означает, что информация, поступающая на вход модели, останется в некоторой степени неопределенной.
Следовательно, первый предложенный подход не ведет к желаемому результату, т. к. нельзя полностью устранить нечеткость информации - для этого требуются бесконечное время и огромные ресурсы. Ни того, ни другого у обычного предприятия с эффективной системой управления нет. Следовательно, необходима разработка системы прогнозирования и управления политикой развития предприятия, основанной на обработке нечетких исходных данных.
Разработка нечеткочисленного метода прогнозирования. Нечеткую исходную информацию можно обрабатывать при помощи общенаучных экспертных методов [18, 17]. Анализируя свойства и области применимости указанных методов, примем за основу метод Дельфи как вносящий наименьшие искажения в обрабатываемую информацию и обладающий максимальной инвариантностью к мнению экспертов.
Метод допускает общее снижение общей погрешности путем уменьшения "погрешности" каждого эксперта. Для этого на выходе метода мы должны получить информацию в виде, максимально приближенном к исходным нечетким данным. Наиболее подходят для указанного представления нечеткие числа. Следовательно, необходимо разработать метод прогнозирования, который будет основой для построения системы управления промышленным предприятием в условиях неопределенности.
В рассматриваемом методе присутствуют два типа преобразования информации, следовательно, два последовательных информационных потока.
Первый этап - от объекта к эксперту - обработка тенденций и выработка результата экспертами.
Второй этап - "подгонка под ответ", т. е. выбор из четкого множества чисел одного, которое дает наибольшую корреляцию с полученным на первом этапе результатом. Искажения, вносимые методом на втором этапе, сводят к минимуму все старания экспертов.
Погрешности преобразования информации  (8.23), которые возникают в классическом методе Дельфи, обусловливают недостаточную эффективность систем управления, основанных на данном методе. В результате решение, принятое лицом, принимающим решения (ЛПР), может оказаться неверным и отрицательно повлиять на устойчивость предприятия.
(8.23), которые возникают в классическом методе Дельфи, обусловливают недостаточную эффективность систем управления, основанных на данном методе. В результате решение, принятое лицом, принимающим решения (ЛПР), может оказаться неверным и отрицательно повлиять на устойчивость предприятия.
Вывод: стадию преобразования информации необходимо исключить из метода в том виде, в каком она присутствует, и заменить более совершенной, ориентированной на работу с нечеткими исходными данными.
Для разработки указанного метода прогнозирования важно представлять себе природу нечеткости информации, которую этот метод должен обрабатывать. В случае прогнозирования развития какойлибо системы имеет место задача о выборе наиболее предпочтительного (с точки зрения эксперта, основывающегося на своем опыте) числа из совокупности. Например, указать срок, когда, по мнению эксперта, появится необходимость в разработке новой линии продукции, оценить длительность внедрения новой технологии, предсказать оптимальную цену принципиально новой разработки.
Все эти вопросы сводятся к выбору из совокупности (множества) данных одного значения. Однако знания эксперта позволяют ему указать лишь область, наиболее реально соответствующую поставленному вопросу, т. е. выделить нечеткое множество, являющееся ответом на вопрос. Для получения "окончательного ответа" в классическом понимании участник опроса вынужден вносить погрешности в свой ответ (вызванные преобразованием нечеткого множества в число).
Чтобы не заставлять экспертов вносить в свои ответы искажения, можно использовать следующий метод прогнозирования, ориентированный на работу с исходными данными, представленными в нечетком виде:
Вход: список вопросов к экспертам,  - число экспертов,
- число экспертов, 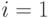 .
.
Шаг 0. Каждому эксперту задают вопрос и просят дать письменный ответ в виде, максимально приближенном к естественному (нечеткого числа треугольной формы).
Выход 0: 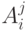 , где
, где  - нечеткое число, выражающее оценку
- нечеткое число, выражающее оценку  -го эксперта на
-го эксперта на  -м этапе метода.
-м этапе метода.
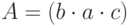 , графическое изображение треугольного нечеткого числа дано на рис. 8.24:
, графическое изображение треугольного нечеткого числа дано на рис. 8.24:
где  - элемент нечеткого множества, имеющее максимальное значение функции принадлежности (в данном случае - нормализованное нечеткое число,
- элемент нечеткого множества, имеющее максимальное значение функции принадлежности (в данном случае - нормализованное нечеткое число,  );
);
 и
и  - ближняя и дальняя граница оценки, соответственно меньше и больше которых функция принадлежности принимает нулевые значения.
- ближняя и дальняя граница оценки, соответственно меньше и больше которых функция принадлежности принимает нулевые значения.
Шаг 1. Производят обработку результатов.
Подсчитываются средние по всем экспертам оценки на  -м этапе:
-м этапе:

и отклонения от среднего значения по каждому эксперту:
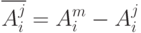
нечеткая сумма вычисляется по формуле:
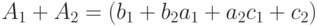
а произведение нечеткого числа на обычное - по формуле
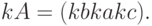
Шаг 2. Участников информируют о результатах предыдущего этапа ( 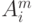 ).
).
Шаг 3. Каждому эксперту опять задают вопрос и просят дать письменный ответ с поправкой на результаты предыдущего этапа.
Выход 3: 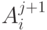 , где
, где  - оценка
- оценка  -го эксперта на
-го эксперта на  -м этапе метода.
-м этапе метода.
Шаг 4. Производят обработку результатов двух последних туров:
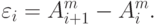
Если процесс сошелся, т. е.
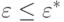
то результат считается достигнутым ( 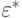 - заранее заданная нечеткая величина, например: "немного больше нуля", "почти ноль", характеризующая необходимую точность метода). Если сходимость отсутствует, шаг 2 повторяется.
- заранее заданная нечеткая величина, например: "немного больше нуля", "почти ноль", характеризующая необходимую точность метода). Если сходимость отсутствует, шаг 2 повторяется.
На выходе получен прогноз в виде нечеткого числа, что хорошо согласуется с неопределенной входной информации. Для дальнейшей обработки прогноза, т. е. принятия решения на его основе, необходимо построить модель функционирования предприятия и разработать систему управления, основанную на нечетких данных.
Структура системы управления должна основываться на структуре внешних воздействий на предприятие. Следовательно, для построения системы управления необходимо проанализировать структуру внешних информационных связей, выделить принципы их взаимодействия, разработать модель функционирования ВПС. На основании модели можно построить структуру системы управления для решения задачи управления, состоящей в сохранении устойчивости предприятия (устойчивой реакции на внешние возмущения), которая влечет за собой устойчивые прибыли и постоянный рост.

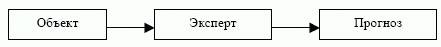

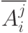 и
и