|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Управление организационно-экономической устойчивостью промышленных корпоративных систем на основе динамического анализа состояния в условиях неопределенности
8.4. Моделирование процессов управления организационно-экономической устойчивостью корпоративных промышленных структур
Построение математической модели функционирования производственной системы. Проанализируем основные принципы взаимодействия систем внутри ВПС, которые позволят принять ряд допущений, полезных при анализе устойчивости ВПС.
В процессе функционирования на предприятие влияют (в большей или меньшей мере) все подсистемы ВПС. Предприятие, в свою очередь, теоретически также может влиять на все остальные подсистемы. Однако в нашей работе воздействия такого рода ( 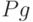 ) (влияние на систему
) (влияние на систему  системы
системы  - в данном случае предприятия на государственные органы) учитывать не будем. В общем виде первый принцип можно сформулировать следующим образом:
- в данном случае предприятия на государственные органы) учитывать не будем. В общем виде первый принцип можно сформулировать следующим образом:
Допущение 1. Системы, имеющие более высокий статус, воздействуют на системы с меньшим рангом, но не наоборот. Системы с одинаковым статусом могут воздействовать друг на друга.
Из этого принципа следует вывод: система распадается на две замкнутые подсистемы:  -
-  -
-  -
- 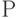 (ПСС) и
(ПСС) и  -
-  -
-  ("внешнюю" по отношению к ПСС). "Внешняя" подсистема имеет более высокий статус, следовательно, воздействие на нее со стороны производственно-сбытовой (или "рыночной") подсистемы отсутствует. Это отображается равенством нулю в табл. 8.7 следующих коэффициентов:
("внешнюю" по отношению к ПСС). "Внешняя" подсистема имеет более высокий статус, следовательно, воздействие на нее со стороны производственно-сбытовой (или "рыночной") подсистемы отсутствует. Это отображается равенством нулю в табл. 8.7 следующих коэффициентов: 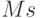 ,
, 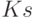 ,
,  ,
, 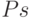 ,
, 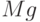 ,
, 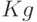 ,
, 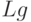 ,
, 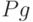 ,
, 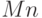 ,
, 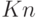 ,
, 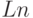 ,
, 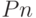 .
.
Рассмотрим теперь функционирование рыночной подсистемы. Второй принцип следует из классического свойства рынка [13]: "спрос рождает предложение". Это дает нам следующее направление воздействий в ПСС: потребитель - производитель - поставщик. Принцип можно сформулировать так:
Допущение 2. Взаимодействуют друг с другом непосредственно только соседние элементы из цепочки "потребитель - производитель - поставщик".
Это значит, что непосредственным воздействием поставщика (  ) на конечного потребителя (
) на конечного потребителя (  ), и наоборот, можно пренебречь. Коэффициенты
), и наоборот, можно пренебречь. Коэффициенты 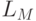 и
и 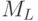 равны.
равны.
Третий принцип получаем, группируя все подсистемы ВПС в два однородных блока: технологический и общественнополитический. В первый входят предприятие ( 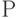 ), конкуренты (
), конкуренты (  ) и поставщики (
) и поставщики (  ), а также воздействующий на них научнотехнический прогресс (
), а также воздействующий на них научнотехнический прогресс (  ). Во второй блок включаем общество (
). Во второй блок включаем общество (  ), государство (
), государство (  ) и потребителей (
) и потребителей (  ). Принцип состоит в следующем утверждении:
). Принцип состоит в следующем утверждении:
Допущение 3. Система непосредственно реагирует на воздействие только однородных систем:
Из этого принципа вытекает независимость предприятий, поставщиков и конкурентов от законов развития общества, а потребителей - непосредственно от научнотехнического прогресса (это отражается отсутствием коэффициентов 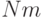 ,
, 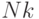 ,
,  и
и 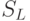 ). В результате получаем табл. 8.7:
). В результате получаем табл. 8.7:
| Воздействия | S | G | N | M | K | L | P |
|---|---|---|---|---|---|---|---|
 |
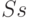 |
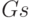 |
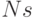 |
0 | 0 | 0 | 0 |
 |
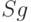 |
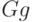 |
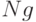 |
0 | 0 | 0 | 0 |
 |
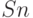 |
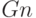 |
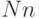 |
0 | 0 | 0 | 0 |
 |
 |
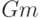 |
0 | 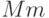 |
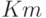 |
0 | 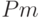 |
 |
 |
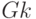 |
0 | 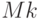 |
 |
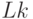 |
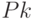 |
 |
0 | 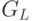 |
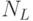 |
0 | 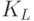 |
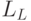 |
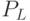 |
 |
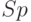 |
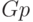 |
0 | 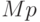 |
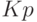 |
 |
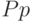 |
В результате проведенного анализа количество учитываемых факторов удалось уменьшить почти на треть (с 49 до 31 матрицы).
Для дальнейшего использования таблицы взаимодействий необходимо разработать методику ее заполнения. Суть коэффициента влияния 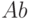 - на сколько изменится вектор состояния системы В при изменении на единицу системы
- на сколько изменится вектор состояния системы В при изменении на единицу системы  , или в математической записи:
, или в математической записи:
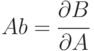
Рассмотрим простейшее дифференциальное уравнение, где точкой над переменной обозначена производная по времени:
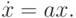
Как известно, коэффициент  имеет следующий смысл:
имеет следующий смысл:
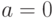 ,
,  - постоянная величина
- постоянная величина
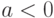 ,
,  - убывает
- убывает
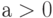 ,
,  - возрастает.
- возрастает.
При 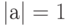 имеем следующее соотношение:
имеем следующее соотношение: 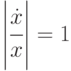 .
.
Таким образом, анализируя связи подсистем, можно определить коэффициенты взаимовлияния, пользуясь следующим алгоритмом.
Шаг 1: определяется, существует ли связь подсистем, т. е. влияет ли изменение одной на состояние другой.
Выход 1.1: нет, не имеется. При изменении одной подсистемы вторая никак не реагирует. Коэффициент влияния равен нулю. Конец алгоритма.
Выход 1.2: да, существует. При изменении вектора состояния первой подсистемы, вектор состояния второй изменился.
Шаг 2: увеличился или уменьшился вектор второй подсистемы.
Выход 2.1: увеличился. Коэффициент взаимовлияния больше нуля.
Выход 2.2: уменьшился. Коэффициент меньше нуля.
Шаг 3: как сильно изменился вектор состояния второй системы от изменения влияемой системы.
Выход 3.1: состояние влияемой подсистемы изменилось сильнее, чем изменилась влияющая. Следовательно, модуль частного от деления приращения вектора состояния влияемой системы на приращение вектора влияющей системы (коэффициент влияния) больше единицы.
Выход 3.2: состояние влияемой подсистемы изменилось в той же мере, что и влияющая. Следовательно, коэффициент влияния равен единице.
Выход 3.3: состояние влияемой подсистемы изменилось меньше, чем влияющей. Коэффициент меньше единицы.
Шаг 4: учитывая промежуточные результаты шагов 1, 2, 3, вычисляем коэффициенты влияния подсистем.
В разделе 8.3 показано, что прогноз развития ВПС является неопределенным, вследствие чего необходимо провести исследование устойчивости получаемого на каждом шаге прогноза под воздействием неопределенных факторов.
Получим уравнения, описывающие взаимодействие элементов производственной системы.
Запишем общие дифференциальные соотношения, имея в виду, что векторы состояния систем являются функциями времени и зависят друг от друга. Вектора состояния являются сложными функциями следующего вида:
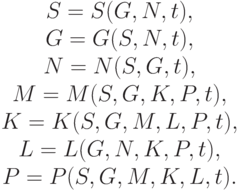 |
( 8.25) |
Эти функции характеризуют состояние соответствующих им систем. Будущее состояние любой системы можно определить, зная ее прошлое (регрессионная модель) либо зная текущее состояние и тенденции развития влияющих на нее систем.
В математических терминах этим понятиям соответствуют значения функции в текущей точке и угол наклона графика функции. В числовом значении угол наклона равен производной функции в данной точке по времени.
Будем обозначать производную по времени точкой над функцией.
Введем О - вектор состояния ВПС следующим образом:
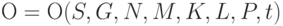
В таком случае можно описать состояние развития общества в динамике следующим уравнением:

т. е. развитие ВПС можно описать дифференциальным уравнением вида:
 |
( 8.26) |
Это консервативная (замкнутая) однородная система дифференциальных уравнений.
Решением такой системы является функция 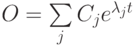 .
.
Здесь  - комплексные числа вида
- комплексные числа вида 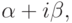 зная которые можно определить устойчива или неустойчива система дифференциальных уравнений. Пользуясь методом Ляпунова, если вещественная часть комплексных собственных чисел отрицательна, то система уравнений устойчива, если хотя бы одно собственное число имеет положительную вещественную часть, то система уравнений неустойчива (этому решению соответствует экспонента).
зная которые можно определить устойчива или неустойчива система дифференциальных уравнений. Пользуясь методом Ляпунова, если вещественная часть комплексных собственных чисел отрицательна, то система уравнений устойчива, если хотя бы одно собственное число имеет положительную вещественную часть, то система уравнений неустойчива (этому решению соответствует экспонента).
Вернемся к нашей модели функционирования ВПС. Зная историю (прошлое) функций, входящих в модель, и свойства (которые могут меняться со временем) самой функции, можно определить тенденции ее развития (матрицу  ).
).
Уравнение (8.26) можно записать подробнее, с учетом табл. 8.7:
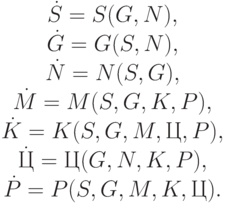 |
( 8.27) |
Видно, что однородная система дифференциальных уравнений распадается на две системы. Первая из них:
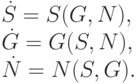 |
( 8.28) |
эта система характеризует развитие систем, имеющих более высокий потенциал, чем предприятие. Вторая система:
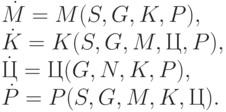 |
( 8.29) |
эта система характеризует развитие ПСС (производственно-сбытовой системы), включающей в себя поставщиков, потребителей и производителей (предприятие и конкурентов).
Как видно, наша модель ВПС распалась на две части: первая (8.28) описывает развитие государства, общества и научнотехнический прогресс; вторая (8.29) - развитие производственно-сбытовой системы.
Проведем анализ системы уравнений, описывающей функционирование производственной системы.
Ранее нами был введен вектор  :
:
Вектор описывает состояния производственной системы в момент времени  .
.
![W = \left [
\begin{array}{ccccccc}
Ss & Gs & Ns & 0 & 0 & 0 & 0 \\
Sg & Gg & Ng & 0 & 0 & 0 & 0 \\
Sn & Gn & Nn & 0 & 0 & 0 & 0 \\
Sm & Gm & Nm & Mm & Km & 0 & Pm \\
Sk & Gk & 0 & Mk & Kk & Цk & Pk \\
0 & Gц & Nц & 0 & Kц & Цц & Pц \\
Sp & Gp & 0 & Mp & Kp & Цp & Pp \\
\end{array}
\right ].](/sites/default/files/tex_cache/c5379c19b3c5bcf004877ecbf60395b6.png) |
( 8.30) |
На основании принятых допущений (табл. 8.7) сформируем матрицу  :
:
 - матрица, характеризующая тенденции развития ВПС в текущий момент времени. Например, элемент
- матрица, характеризующая тенденции развития ВПС в текущий момент времени. Например, элемент 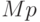 описывает влияние вектора
описывает влияние вектора  на изменение вектора
на изменение вектора  , т. е. влияние поставщиков на предприятие (табл. 8.8).
, т. е. влияние поставщиков на предприятие (табл. 8.8).
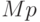 |
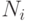 |
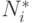 |
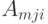 |
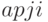 |
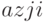 |
|---|---|---|---|---|---|
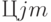 |
Mp11 | Mp12 | Mp13 | Mp14 | Mp15 |
 |
Mp21 | Mp22 | Mp23 | Mp24 | Mp25 |
 |
Mp31 | Mp32 | Mp33 | Mp34 | Mp35 |
 |
Mp41 | Mp42 | Mp43 | Mp44 | Mp45 |
 * * |
Mp51 | Mp52 | Mp53 | Mp54 | Mp55 |
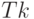 |
Mp61 | Mp62 | Mp63 | Mp64 | Mp65 |
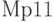 - изменение объемов выпуска предприятием продукции за единицу времени, вызванное увеличением на единицу цен поставщика.
- изменение объемов выпуска предприятием продукции за единицу времени, вызванное увеличением на единицу цен поставщика.
 - изменение объемов выпуска предприятием продукции за единицу времени, вызванное увеличением на единицу времени доставки сырья поставщиком.
- изменение объемов выпуска предприятием продукции за единицу времени, вызванное увеличением на единицу времени доставки сырья поставщиком.
 - изменение материалоемкости продукции предприятия за единицу времени, обусловленное увеличением на единицу величины партии поставщика.
- изменение материалоемкости продукции предприятия за единицу времени, обусловленное увеличением на единицу величины партии поставщика.
Уравнения развития ВПС можно записать так:
 |
( 8.31) |
где точкой над функцией обозначена производная по времени, а матрица рядом с вектором обозначает скалярное произведение матрицы на вектор.
Пользуясь табл. 8.7 можно расчленить ВПС на Внешнюю и Рыночную подсистемы. Для этого разделяем вектор состояния  и матрицу влияния
и матрицу влияния  на части, соответствующие указанным системам:
на части, соответствующие указанным системам:
![W =
\left [
\begin{array}{ccccccccc}
Ss & Gs & Ns & | & Ms & Ks & Цs & | & P \\
Sg & Gg & Ng & | & Mg & Kg & Цg & | & P \\
Sn & Gn & Nn & | & Mn & Kn & Цn & | & Pn \\
-- & -- & -- & + & -- & -- & -- & + & -- \\
Sm & Gm & Nm & | & Mm & Km & Цm & | & Pm \\
Sk & Gk & Nk & | & Mk & Kk & Цk & | & Pk \\
Sц & Gц & Nц & | & Mц & Kц & Цц & | & Pц \\
-- & -- & -- & + & -- & -- & -- & + & -- \\
Sp & Gp & Np & | & Mp & Kp & Цp & | & Pp
\end{array}
\right ]
\\
\vec {O}(t) =
\left \{
\begin{array}{c}
\vec S \\
\vec G \\
\vec N \\
-- \\
\vec M \\
\vec K \\
\vec Ц \\
-- \\
\vec P \\
\end{array}
\right \}](/sites/default/files/tex_cache/83f2dc16f24061265b37b0358fa25a22.png) |
( 8.32) |
Тогда можно ввести следующие вектора состояний:
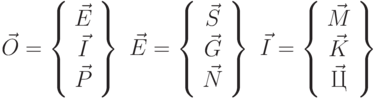
![W =
\left [ \begin{array}{ccc}
Ee & Ie & Pe \\
Ei & Ii & Pi \\
Ep & Ip & Pp \\
\end{array} \right ]
Ee =
\left [ \begin{array}{ccc}
Ss & Gs & Ns \\
Sg & Gg & Ng \\
Sn & Gn & Nn \\
\end{array} \right ]
Ei =
\left [ \begin{array}{ccc}
Sm & Gm & Nm \\
Sk & Gk & Nk \\
Sц & Gц & Nц \\
\end{array} \right ]
Ep =
\left [ \begin{array}{ccc}
Sp & Gp & Np \\
\end{array} \right ]
Ii =
\left [ \begin{array}{ccc}
Mm & Km & Цm \\
Mk & Kk & Цk \\
Mц & Kц & Цц \\
\end{array} \right ]
Ip =
\left [ \begin{array}{ccc}
Mp & Kp & Цp \\
\end{array} \right ]
Pi =
\left [ \begin{array}{c}
Pm \\
Pk \\
Pц \\
\end{array} \right ]
Pp = [Pp]](/sites/default/files/tex_cache/6f48b1a11eab8b197fc8f1a089a105c3.png)
Введенные вектора и матрицы имеют следующий смысл:
 - вектор состояния внешней системы;
- вектор состояния внешней системы;
 - вектор состояния рыночной системы;
- вектор состояния рыночной системы;
 - вектор состояния предприятия;
- вектор состояния предприятия;
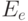 - матрица влияния компонентов внешней системы друг на друга;
- матрица влияния компонентов внешней системы друг на друга;
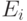 - матрица влияния внешней системы на рыночную систему;
- матрица влияния внешней системы на рыночную систему;
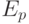 - матрица влияния внешней системы на предприятие;
- матрица влияния внешней системы на предприятие;
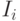 - матрица влияния компонент рыночной системы друг на друга;
- матрица влияния компонент рыночной системы друг на друга;
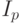 - матрица влияния рыночной системы на предприятие;
- матрица влияния рыночной системы на предприятие;
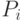 - матрица влияния предприятия на рыночную систему;
- матрица влияния предприятия на рыночную систему;
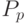 - коэффициент, характеризующий управление предприятием.
- коэффициент, характеризующий управление предприятием.
Матрицы 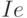 и
и 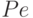 - нулевые, согласно принятым выше допущениям. Коэффициенты
- нулевые, согласно принятым выше допущениям. Коэффициенты 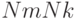
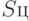


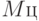 также равны нулю (табл. 8.7). Запишем соотношения между вновь введенными векторами и вектором состояния
также равны нулю (табл. 8.7). Запишем соотношения между вновь введенными векторами и вектором состояния  ; между матрицами влияния систем и матрицей
; между матрицами влияния систем и матрицей  :
:
![\dot{\vec E} = [Ee]\vec E \\
\dot{\vec I} = [Ei]\vec E + [Ii ] \vec I + [Pi] \vec P \\
\dot{\vec P} = [Ep]\vec E + [Ip]\vec I + [Pp]\vec P.](/sites/default/files/tex_cache/99b32864e09a58ff23b79348fd056480.png) |
( 8.33) |
Уравнения (8.33) суть система дифференциальных уравнений. Они описывают развитие ВПС в динамике:
- первое уравнение характеризует развитие внешней системы.
- второе уравнение описывает изменение рыночной системы под воздействием внешней системы и предприятия.
- третье - уравнение развития предприятия.
Рассмотрим частные случаи функционирования ВПС:
- Возмущения внешней системы отсутствуют (
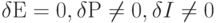 ).
).![\begin{array}{c}
(\dot{\vec{E}})= [Ei] \dot{\vec{E}}, \\
(\dot{\vec{I}}+ \delta \dot{\vec{I}}) = [Ei] \vec{I}+ [Ii](\vec{I}+ \delta \vec{I}) + [Pi](\vec{P} + \delta \vec{P}), \\
(\dot{\vec{P}}+ \delta \dot{\vec{P}}) = [Ep] \vec{E}+ [Ip](\vec{I}+ \delta \vec
{I}) + [Pp][\vec{P} + \delta \vec{P}].
\end{array}](/sites/default/files/tex_cache/ad0ef4981fc6657e1dd37f9176c72216.png)
Уравнения в возмущениях записываются следующим образом:
![\delta \dot{\vec {I}} = [Ii]\delta \vec{I} + [Pi]\delta \vec{P}, \\
\delta \dot{\vec {P}} = [Ip]\delta \vec{I} + [Pp]\delta \vec{P}.](/sites/default/files/tex_cache/84b0d9df6f8934ce81608c540744644a.png)
( 8.34) - Возмущающий фактор - внешняя система (
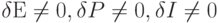 ). В этом случае уравнения в возмущениях запишутся так:
). В этом случае уравнения в возмущениях запишутся так:![\delta \dot{\vec{E}} = [Ee]\delta \vec{ E}, \\
\delta \dot{\vec{I}} = [Ei]\delta \vec{E} + [Ii]\delta \vec{I}, \\
\delta \dot{\vec{P}} = [Ep]\delta \vec{ E} + [Pp]\delta \vec{P}.](/sites/default/files/tex_cache/28577f3fd5aa1b2f64a13703bae91ee4.png)
( 8.35) Уравнения (8.34) и (8.35) позволяют провести исследование устойчивости предприятия.