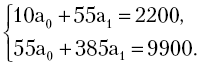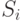Анализ производства и отгрузки продукции (работ, услуг). Анализ финансовых результатов. Основные направления долгосрочного инвестирования
1.5. Методика оптимизации прибыли (предельный анализ)
Получение максимальной прибыли возможно при определенном сочетании объема производства, цены продукта и издержек на его производство и реализацию. При принятии управленческих решений, нацеленных на увеличение прибыли предприятия, необходимо учитывать предполагаемые величины предельного дохода и предельных издержек. Предельный доход - это прирост выручки от реализации на единицу прироста количества произведенной продукции. Соответственно предельные издержки равны приросту затрат на производство продукции, приходящемуся на единицу прироста количества произведенной продукции. Для получения максимальной прибыли необходимо равенство предельных издержек и предельного дохода.
Введем следующие условные обозначения:
| q | - | количество продукции; |
| Z | - | цена единицы продукции; |
| Z x q | - | доход (выручка) от реализации продукции; |
| S | - | издержки производства (затраты); |
| Р | - | прибыль от реализации. |
Тогда стремление получить максимум прибыли может быть представлено в формальном виде следующей функцией:
.Применение предельного подхода к этой функции дает следующее соотношение:
Отсюда следует: чтобы прибыль была максимальной, необходимо равенство предельного дохода и предельных издержек, а также отрицательный знак второй производной прибыли по количеству продукции:
Это соотношение позволяет найти оптимальный размер объема производства при известных (или заданных) функциях цены: Z = f(q) и издержек: S = g(q).
Проведем анализ на оптимальность объема производства по предприятию. Предприятие должно найти такой объем производства продукции, при котором оно извлекло бы наибольший доход.
В данном разделе рассмотрены несколько вариантов проведения предельного анализа, предложенных в книге Г.В. Савицкой "Анализ хозяйственной деятельности предприятия", и способ, изложенный в книге А.Д. Шеремета, Е.В. Негашева, Р.С. Сайфулина "Методика финансового анализа". Согласно Г.В. Савицкой, существует несколько способов определения оптимального объема производства: бухгалтерско-аналитический; графический; статистический.
Сущность бухгалтерско-аналитического способа состоит в сопоставлении предельного дохода и предельных издержек. Если предельный доход больше предельных издержек, то дальнейший рост выпуска продукции увеличивает общую сумму прибыли, и наоборот. Следовательно, для максимизации прибыли предприятие должно расширять объем производства до тех пор, пока предельный доход выше предельных издержек, и прекратить расширение производства, как только предельные издержки начнут превосходить предельный доход.
Данные табл. 1.11 показывают, что самый выгодный объем производства при 7 тыс. шт. изделий. Затем предельные издержки уже превосходят предельный доход, что явно неблагоприятно для предприятия. Следовательно, до 7 тыс. шт. предприятию выгодно производить продукцию, но сверх этой величины производство неэффективно.
Сущность статистического метода заключается в том, что на основании массовых данных исследуется зависимость предельного дохода и предельных издержек от объема реализации продукции.
Проведем анализ на оптимальность объема продукции, используя данные табл. 1.12.
| Объем продукции, тыс. шт., q | Цена, руб., Z | Общий доход (выручка), тыс. руб., Z x q | Общие издержки, тыс. руб., S | Прибыль, тыс. руб., Р | Предельный доход, тыс. руб., d(Z x q) | Предельные издержки, тыс. руб., dS |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 0 | 250 | 0 | 210 | -210 | - | - |
| 1 | 240 | 240 | 350 | -110 | 240 | 140 |
| 2 | 230 | 460 | 480 | -20 | 220 | 130 |
| 3 | 220 | 660 | 600 | +60 | 200 | 120 |
| 4 | 210 | 840 | 710 | +130 | 180 | 110 |
| 5 | 200 | 1 000 | 810 | +190 | 160 | 100 |
| 6 | 190 | 1140 | 915 | +225 | 140 | 105 |
| 7 | 180 | 1 260 | 1 030 | +230 | 120 | 115 |
| 8 | 170 | 1 360 | 1 155 | +205 | 100 | 125 |
| 9 | 160 | 1 440 | 1 300 | +140 | 80 | 140 |
| 10 | 150 | 1 500 | 1 450 | +45 | 60 | 155 |
Анализ зависимости между ценой и количеством продукции в динамике позволяет выбрать для функции спроса линейную форму связи вида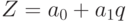 
. По методу наименьших квадратов определяются неизвестные параметры 
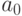и 
на основе составления и решения системы нормальных уравнений вида
| где | n | - | число наблюдений (лет); |
 |
- | количество продукции в натуральном выражении, шт.; | |
 |
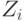- | цена единицы продукции, руб. |
Решение.
Разделив показатели первого уравнения на 10, а второго на 55, получим
Вычтя из первого уравнения второе, получим: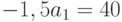 
, отсюда 
.
Подставим это выражение в первое уравнение, получим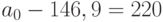 
, отсюда 
.
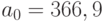После проведения расчетов получим эмпирическую функцию спроса
Z = 366,9 - 26,7q.
Анализ зависимости между издержками и количеством продукции в динамике позволяет для функции издержек выбрать также линейную форму связи вида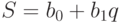 
. Неизвестные параметры 
и 
также находятся по методу наименьших квадратов путем составления и решения системы нормальных уравнений вида:
Решение.
Разделив показатели первого уравнения на 10, а второго на 55, получим:
Вычтя из первого уравнения второе, получим: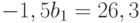 
, отсюда 
. Подставив это выражение в первое уравнение, получим: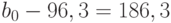 
, отсюда 
.
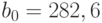В окончательном виде имеем следующую эмпирическую функцию издержек:
S = 282,6 - 17,5q.
Теперь проведем расчеты предельного дохода и предельных издержек и, приравнивая их друг к другу, найдем величину оптимального объема продукции:
Z = 366,9 - 26,7q;
S = 282,6 - 17,5q;
;
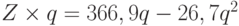366,9 - 53,4q = -17,5, или 366,9 + 17,5 = 53,4q, т. е. q = 384,4 : 53,4 = 7,2 тыс. шт.
Приведенные расчеты показывают, что оптимальный объем продукции составляет 7,2 тыс. шт.
При таком объеме выручка от реализации составит
Z x q = 180 x 7,2 = 1 296 тыс. руб.
Издержки производства и реализации продукции:
S x q = (1 030 : 7) x 7,2, или 147 · 7,2 = 1 058 тыс. руб.
Прибыль:
Р = Z x q - S x q = 1 296 - 1 058 = 238 тыс. руб.
Следовательно, данному предприятию нужно придерживаться стратегии наращивания объема продукции до 7,2 тыс. шт. при условии, что себестоимость его продукции существенно не повысится в ближайшей перспективе.
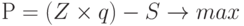