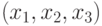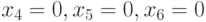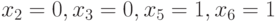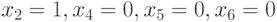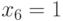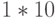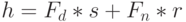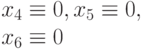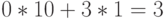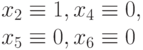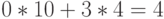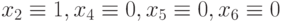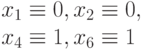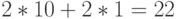Эволюционные методы генерации тестов

25.2 Генетические алгоритмы в генерации тестов для комбинационных схем

Классический "простой" генетический алгоритм [25.1] использует двоичные стринги - строки из двоичных элементов 0,1 (например, 0011101), что делает его привлекательным для задач генерации проверяющих тестов логических схем, где решение представляется в виде двоичных наборов или их последовательностей, которые в данном случае рассматриваются как особи популяции - множества возможных решений [25.2]. На множестве решений определяется целевая (fitness) функция (ЦФ), которая позволяет оценить близость каждой особи к оптимальному решению. В случае задачи генерации тестов ЦФ прямо или косвенно должна отражать такие свойства двоичных наборов или последовательностей как число проверяемых неисправностей или изменений сигналов в схеме.

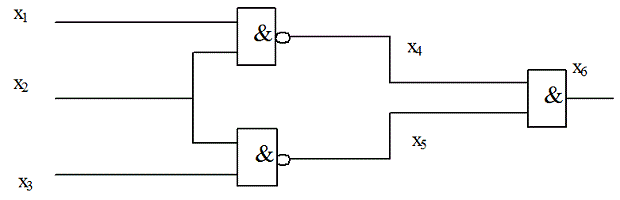
Рассмотрим простейший случай использования ГА для генерации тестов комбинационных схем[25.3]. Очевидно, особью (хромосомой) в данном случае является отдельный двоичный набор значений входных переменных 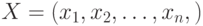, где и равно числу входов схемы. Популяцией является множество наборов, составляющих проверяющий тест схемы. Обычно число особей в популяции пропорционально числу входов (например, 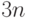) В качестве целевой (fitness) функции пока для простоты (условно) для каждого двоичного набора будем считать число проверяемых им неисправностей. Следует подчеркнуть, что значение ЦФ определяется с помощью программы логического моделирования, которая является важнейшей компонентой этого метода. Мы рассмотрим применение ГА для генерации тестов на примере схемы рис. 25.3. Для удобства в табл. 25.1 представлены все возможные 8 входных наборов со значениями сигналов на всех линиях схемы рис. 25.3.

При инициализации популяция входных векторов генерируется случайным образом. Для нашего примера рис. 25.3 начальная популяция (построенная случайно) представлена в первом столбце табл. 25.2. Во втором столбце для каждой особи - набора показаны проверяемые им одиночные константные неисправности. Очевидно, что входной набор, проверяющий большее количество неисправностей, должен иметь больше шансов попасть в тестовое множество.

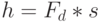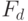Поэтому на начальном этапе в качестве фитнеcc-функции можно взять , где - число (вновь) проверяемых неисправностей и - "премия" за каждую проверенную неисправность (в нашем примере 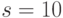). В реальной системе генерации тестов 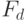определяется с помощью моделирования неисправностей. Очевидно, лучший входной набор (011 или 101) с максимальным значением фитнеcc-функции 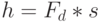должен быть включен в тест. Пусть для определенности это будет набор (101). Далее для генерации популяции следующего поколения необходимо применить генетические операторы кроссинговера и мутации.

Рис. 25.3. Комбинационная схема для построения теста с использованием ГА

Таблица 25.1.

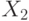
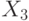
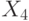
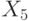
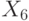
0	0	0	1	1	1
0	0	1	1	1	1
0	1	0	1	1	1
0	1	1	1	0	0
1	0	0	1	1	1
1	0	1	1	0	0
1	1	0	0	1	0
1	1	1	0	1	0

Таблица 25.2.

Входной набор	Проверяемые неисправности	Значение фитнесс-функции
000
011
101
111

При одноточечном кроссинговере случайно выбирается точка скрещивания с вероятностью и производится обмен фрагментами хромосом после точки скрещивания. Например, для двух родительских особей (0Ѕ11) (1Ѕ01) с точкой к=1 получаем два потомка - наборы (0Ѕ01) (1Ѕ11).

При двухточечном кроссинговере потомки наследуют фрагменты хромосом родителей между двумя случайно выбранными точками скрещивания, как это показано, например, на рис. 25.4.

Рис. 25.4. Пример двухточечного кроссинговера

После выполнения операторов кроссинговера полученные потомки с вероятностью 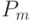подвергаются мутации, которая может быть выполнена различными способами. В простейшем случае для каждой особи случайно выбирается позиция и с малой вероятностью от 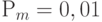до 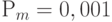выполняется инвертирование значения переменной в выбранной позиции.

Каждую особь популяции нового поколения необходимо оценить с помощью фитнесс-функции, которая в общем случае (кроме начальной популяции) должна в первую очередь учитывать число вновь проверенных данным набором неисправностей. Допустим, что после второго шага в текущее тестовое множество включены два входных набора (101,011), которые проверяют (и не проверяют неисправности, показанные в табл. 25.3) и текущая популяция входных наборов (кандидатов на включение в тест) представлена в табл. 25.4.

Таблица 25.3.

Тестовое множество	Проверенные неисправности	Непроверенные неисправности текущим тестом
101
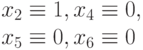
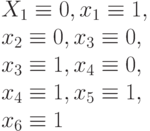
011

Таблица 25.4.

Входной набор	Проверяемые неисправности	Значение фитнесс-функции
000
001
100
110

Таблица 25.5.

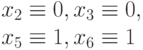
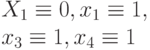
Тестовое множество	Проверенные неисправности	Непроверенные неисправности текущим тестом
101
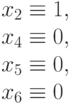
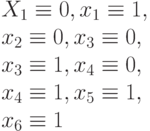
011
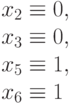
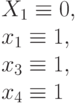
110

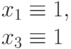
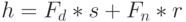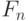Заметим, что далее мы используем фитнесс-функцию , где - число вновь проверенных неисправностей и 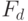- число ранее проверенных неисправностей соответствующим тестовым набором. Здесь 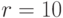- премия за каждую вновь проверенную неисправность и 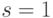- премия за каждую ранее проверенную неисправность. В соответствие с данными табл. 25.4 тестовый набор (110) должен быть включен в тестовую последовательность поскольку он имеет максимальное значение фитнесс-функции. В следующей табл. 25.5 ситуация показана для текущего тестового множества, которое состоит из трех наборов и имеет только две непроверяемые неисправности.

Аналогично можно показать, что на следующем шаге тестовый набор (010) должен быть включен в тест, поскольку он проверяет последнии непроверенные неисправности 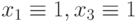. Укрупненный генетический алгоритм на основе описанного подхода представлен псевдокодом рис. 25.5.

Здесь на этапе инициализации генерируется множество неисправностей, и выполняются другие вспомогательные операции. Обычно наборы начальной популяции генерируются случайным образом, но если априорная доступная информация о хороших кандидатах в тест, то она может быть использована. Оценка значений фитнесс-функции выполняется на основе данных логического моделирования с неисправностями. Заметим, что в описанном выше подходе генетический алгоритм на каждом шаге решает локальную проблему поиска особи - следующего входного набора для включения его в тест в отличие от классичекого ГА, где особь представляет глобальное решение проблемы (весь тест).

Рис. 25.5. Псевдокод генетического алгоритма генерации тестов для комбинационных схем

В следующем разделе мы рассмотрим глобальный подход к использованию ГА в генерации теста для последовательностных схем, где особь представляет всю тестовую последовательность, а не один входной набор.