|
Добрый день можно поинтересоваться где брать литературу предложенную в курсе ?Большинство книг я не могу найти в известных источниках |
Структурное построение тестов для устройств с памятью
23.2 Построение тестов для последовательностных схем в 16-значном алфавите
Большинство структурных методов построения тестов последовательностных схем для активизации критических путей в схеме используют многозначные алфавиты [23.1-23.3].
Последние позволяют с различной точностью описывать возможные комбинации значений сигналов в исправном и неисправном ЦУ. В
"Система многозначных алфавитов и функций"
рассматривался универсальный 16-значный алфавит  (табл. 7.1), элементами которого являются всевозможные подмножества алфавита
(табл. 7.1), элементами которого являются всевозможные подмножества алфавита 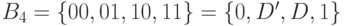 , и который покрывает основные многозначные алфавиты, используемые в методах диагностики ЦУ на структурном уровне [23.1-23.3]. Как, указывалось в
"Многомерная активизация путей в шестизначном алфавите"
, элементы этого алфавита, в контексте задачи построения проверяющих тестов, имеют следующую интерпретацию:
, и который покрывает основные многозначные алфавиты, используемые в методах диагностики ЦУ на структурном уровне [23.1-23.3]. Как, указывалось в
"Многомерная активизация путей в шестизначном алфавите"
, элементы этого алфавита, в контексте задачи построения проверяющих тестов, имеют следующую интерпретацию: 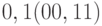 - значения сигналов одинаковы,
- значения сигналов одинаковы,  - значения сигналов различны в исправном и неисправном ЦУ.
- значения сигналов различны в исправном и неисправном ЦУ.
Основные многозначные алфавиты, используемые при генерации тестов, также являются подмножествами универсального алфавита 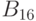 (
"Многомерная активизация путей в шестизначном алфавите"
-
"Построение тестов с использованием алфавитов большой значности"
).
Так, наиболее распространенные на практике современные модификации
(
"Многомерная активизация путей в шестизначном алфавите"
-
"Построение тестов с использованием алфавитов большой значности"
).
Так, наиболее распространенные на практике современные модификации  -алгоритма [23.1,23.2], метод PODEM [23.4] и его дальнейшее развитие - метод FAN [23.5], используют шестизначный алфавит
-алгоритма [23.1,23.2], метод PODEM [23.4] и его дальнейшее развитие - метод FAN [23.5], используют шестизначный алфавит 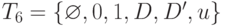 (здесь и далее символ \varnothing используется для обозначения конфликтных ситуаций). В общем случае эти методы требуют многомерной активизации путей (распространения значений
(здесь и далее символ \varnothing используется для обозначения конфликтных ситуаций). В общем случае эти методы требуют многомерной активизации путей (распространения значений 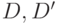 по нескольким путям одновременно).
по нескольким путям одновременно).
Следующая группа методов типа "9V" [23.6] (один из методов изложен в
"Построение тестов с использованием алфавитов большой значности"
) использует десятизначный алфавит 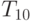 ,который, кроме символов, входящих в
,который, кроме символов, входящих в 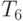 , содержит символы
, содержит символы 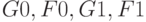 , позволяющие более точно описывать возможные комбинации значений сигналов. К ним относится также метод, основанный на SPLIT-модели, который использует фактически 12-значный алфавит
, позволяющие более точно описывать возможные комбинации значений сигналов. К ним относится также метод, основанный на SPLIT-модели, который использует фактически 12-значный алфавит 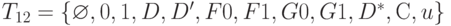 [23.7]. Благодаря использованию более мощных алфавитов, этим методам для построения теста достаточно одномерной активизации путей в схеме.
Следует отметить, что чем больше мощность алфавита, тем дальше удается отодвинуть "перебор" вариантов и тем самым сузить пространство поиска в процессе генерации тестового набора. В этом смысле универсальный алфавит
[23.7]. Благодаря использованию более мощных алфавитов, этим методам для построения теста достаточно одномерной активизации путей в схеме.
Следует отметить, что чем больше мощность алфавита, тем дальше удается отодвинуть "перебор" вариантов и тем самым сузить пространство поиска в процессе генерации тестового набора. В этом смысле универсальный алфавит 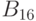 представляет существенно большие возможности, чем остальные рассмотренные алфавиты. Поэтому по мере развития методов построения тестов значность используемых алфавитов постоянно растет. Далее мы рассмотрим метод построения тестов для последовательностных схем в 16-значном алфавите, который является развитием метода, изложенного в
"Построение тестов с использованием алфавитов большой значности"
.
представляет существенно большие возможности, чем остальные рассмотренные алфавиты. Поэтому по мере развития методов построения тестов значность используемых алфавитов постоянно растет. Далее мы рассмотрим метод построения тестов для последовательностных схем в 16-значном алфавите, который является развитием метода, изложенного в
"Построение тестов с использованием алфавитов большой значности"
.
Как было сказано выше, наиболее распространенный на практике подход к построению тестов для последовательностных устройств основан на преобразовании его в так называемый комбинационный эквивалент, получаемый путем условного обрыва обратных связей [23.1-23.3,23.6,23.8-23.11]. При построении теста для данной неисправности проводится активизация путей с помощью многозначных алфавитов до одного из выходов последней копии ИКС.
Число копий  определяется из условий активизации путей и при необходимости может наращиваться. Различают два основных подхода к решению этой задачи: прямой и обратный [23.7-23.10]. В большинстве случаев применяется обратный подход, при котором в случае невозможности решения задачи при данном числе копий они наращиваются в обратном направлении (от
определяется из условий активизации путей и при необходимости может наращиваться. Различают два основных подхода к решению этой задачи: прямой и обратный [23.7-23.10]. В большинстве случаев применяется обратный подход, при котором в случае невозможности решения задачи при данном числе копий они наращиваются в обратном направлении (от  до
до  ,
,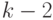 и т. д.). Пример обратного подхода приведен в предыдущем
"Структурное построение тестов для устройств с памятью"
данной лекции (рис. 23.5, 23.6).
и т. д.). Пример обратного подхода приведен в предыдущем
"Структурное построение тестов для устройств с памятью"
данной лекции (рис. 23.5, 23.6).
При прямом подходе копии наращиваются в прямом порядке (от  ко
ко 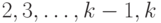 ). Иногда применяется и смешанная стратегия. Например, процедура D-распространения выполняется в прямом порядке, а процедура подтверждения и установки схемы в необходимое состояние в обратном порядке. Каждый из этих подходов имеет свои преимущества и недостатки.
). Иногда применяется и смешанная стратегия. Например, процедура D-распространения выполняется в прямом порядке, а процедура подтверждения и установки схемы в необходимое состояние в обратном порядке. Каждый из этих подходов имеет свои преимущества и недостатки.
Мы будем применять прямой подход и метод генерации тестов в универсальном алфавите 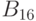 [23.12]. Несмотря на то, что прямое наращивание применяется реже, в сочетании с алфавитом
[23.12]. Несмотря на то, что прямое наращивание применяется реже, в сочетании с алфавитом 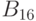 эта стратегия более естественна, эффективна и перспективна. Тандем 16-значного алфавита и прямой стратегии позволяет избежать в явном виде решения трудоемкой задачи установки ЦУ в заданное состояние, сохранить значения переменных состояния исправной схемы при переходе к следующей временной копии и проще в реализации, поскольку является прямым обобщением метода генерации тестов для комбинационных ЦУ, изложенного в
"Построение тестов с использованием алфавитов большой значности"
, и требует меньшего числа дополнительных процедур. С другой стороны, этот подход при реализации использует больше оперативной памяти.
эта стратегия более естественна, эффективна и перспективна. Тандем 16-значного алфавита и прямой стратегии позволяет избежать в явном виде решения трудоемкой задачи установки ЦУ в заданное состояние, сохранить значения переменных состояния исправной схемы при переходе к следующей временной копии и проще в реализации, поскольку является прямым обобщением метода генерации тестов для комбинационных ЦУ, изложенного в
"Построение тестов с использованием алфавитов большой значности"
, и требует меньшего числа дополнительных процедур. С другой стороны, этот подход при реализации использует больше оперативной памяти.
Когда начинается процесс генерации теста, неизвестно, какое из четырех значений алфавита 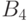 может иметь место, и предполагается, что на каждой линии устройства возможны любые комбинации значений сигналов:
может иметь место, и предполагается, что на каждой линии устройства возможны любые комбинации значений сигналов: 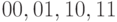 . Поэтому сначала всем линиям схемы присваивается неопределенное значение u алфавита
. Поэтому сначала всем линиям схемы присваивается неопределенное значение u алфавита 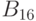 .
Затем, используя свойства структуры схемы и знание местоположения данной неисправности, исключают ненужные (или невозможные) комбинации сигналов для линий ЦУ, снимая, таким образом, неопределенность. Прежде всего всем линиям схемы, на которые неисправность не оказывает влияния, необходимо присвоить значение
.
Затем, используя свойства структуры схемы и знание местоположения данной неисправности, исключают ненужные (или невозможные) комбинации сигналов для линий ЦУ, снимая, таким образом, неопределенность. Прежде всего всем линиям схемы, на которые неисправность не оказывает влияния, необходимо присвоить значение  (возможны только две комбинации
(возможны только две комбинации 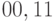 ). Описанные действия называются структурной импликацией.
После этого необходимо внести влияние неисправности. Для этого можно выполнить условный разрыв на неисправной линии
). Описанные действия называются структурной импликацией.
После этого необходимо внести влияние неисправности. Для этого можно выполнить условный разрыв на неисправной линии  и присвоить начальные значения
и присвоить начальные значения 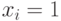 до разрыва и
до разрыва и  после разрыва для константной неисправности
после разрыва для константной неисправности  и соответственно
и соответственно  до разрыва и
до разрыва и  после разрыва для константной неисправности
после разрыва для константной неисправности 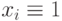 (иногда целесообразно присваивать значения
(иногда целесообразно присваивать значения 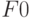 и
и 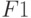 вместо
вместо  и
и 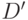 ) [23.1,23.12].
) [23.1,23.12].
При структурной импликации учитывались только топологические свойства схемы. Кроме того, необходимо использовать и свойства логических элементов [23.1,23.12]. Это делается с помощью логической импликации, которая заключается в следующем. Рассмотрим вентиль 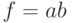 , содержащийся внутри некоторой схемы. Пусть в результате предыдущих действий его входы и выход имеют следующие значения:
, содержащийся внутри некоторой схемы. Пусть в результате предыдущих действий его входы и выход имеют следующие значения: 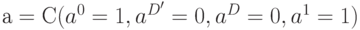 ,
,  и
и 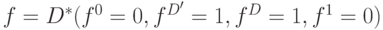 . С помощью прямых многозначных функций из табл. 7.5 (
"Система многозначных алфавитов и функций"
) для вентиля "И" получаем новые значения
. С помощью прямых многозначных функций из табл. 7.5 (
"Система многозначных алфавитов и функций"
) для вентиля "И" получаем новые значения
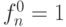 ,
, 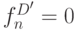 ,
, 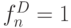 ,
, 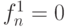 , т.е.
, т.е.  . Выполнив пересечение кодов старого и нового значений с помощью покомпонентной конъюнкции, получим
. Выполнив пересечение кодов старого и нового значений с помощью покомпонентной конъюнкции, получим
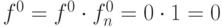 ,
,
 ,
,
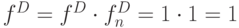 ,
,
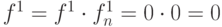 .
Таким образом, в результате прямой логической импликации неопределенность на выходе вентиля уменьшилась до единственной комбинации
.
Таким образом, в результате прямой логической импликации неопределенность на выходе вентиля уменьшилась до единственной комбинации 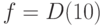 . Если в результате покомпонентной конъюнкции получается символ
. Если в результате покомпонентной конъюнкции получается символ  -
- 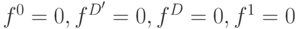 , то это говорит о конфликтной ситуации (невозможность ни одной из четырех комбинаций). Аналогично прямая импликация выполняется и для других элементов.
, то это говорит о конфликтной ситуации (невозможность ни одной из четырех комбинаций). Аналогично прямая импликация выполняется и для других элементов.
Для обратной импликации следует использовать обратные функции 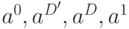 из табл. 7.7 (
"Система многозначных алфавитов и функций"
), которые позволяют по заданным значениям выхода и одного из входов получить значение второго входа. Поскольку входы основных вентилей симметричны, то функции для второго входа можно получить из функций первого простой заменой переменных. Продолжим наш пример для вентиля "И". Проведя обратную импликацию для входа
из табл. 7.7 (
"Система многозначных алфавитов и функций"
), которые позволяют по заданным значениям выхода и одного из входов получить значение второго входа. Поскольку входы основных вентилей симметричны, то функции для второго входа можно получить из функций первого простой заменой переменных. Продолжим наш пример для вентиля "И". Проведя обратную импликацию для входа  , получим:
, получим:
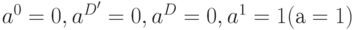 . В данном случае неопределенность на входе
. В данном случае неопределенность на входе  также уменьшилась до одной комбинации -
также уменьшилась до одной комбинации - 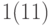 . Далее, считая значения
. Далее, считая значения  и
и  известными, выполняем обратную импликацию для второго входа
известными, выполняем обратную импликацию для второго входа  и получаем:
и получаем:
 . Таким образом, в результате прямой и обратной логической импликации на вентиле установились все определенные значения.
. Таким образом, в результате прямой и обратной логической импликации на вентиле установились все определенные значения.
Процедуры логической импликации применяются после структурной импликации и в процессе генерации теста, когда надо снять неопределенность в результате выбора некоторого варианта в дереве решений. Импликация выполняется до тех пор, пока значения сигналов не стабилизируются. Порядок, в котором проводится импликация, не имеет значения для конечного результата установившихся значений, но влияет на время выполнения. Здесь могут применяться различные стратегии.
Далее с помощью описанных выше процедур необходимо, насколько возможно, снять неопределенность и попытаться распространить значения  или
или 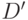 до одного из внешних выходов итеративной комбинационной схемы
до одного из внешних выходов итеративной комбинационной схемы 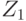 . В общем случае при этом значения псевдовходов
. В общем случае при этом значения псевдовходов 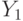 должны оставаться равными
должны оставаться равными 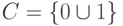 (если неисправность не расположена на линиях обратных связей).
Если же вследствие импликации хотя бы одна из переменных
(если неисправность не расположена на линиях обратных связей).
Если же вследствие импликации хотя бы одна из переменных 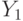 примет значение 0 или 1, то это означает конфликт по переменным состояний и необходимо искать другое решение. Если для первой копии не удастся распространить значения
примет значение 0 или 1, то это означает конфликт по переменным состояний и необходимо искать другое решение. Если для первой копии не удастся распространить значения  ,
, 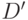 до одного из внешних выходов
до одного из внешних выходов 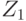 , необходимо в ИКС добавить вторую копию комбинационного эквивалента и попытаться получить
, необходимо в ИКС добавить вторую копию комбинационного эквивалента и попытаться получить  ,
, 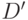 на выходах второй копии ИКС.
В случае неудачи этот процесс продолжается до тех пор, пока на выходе
на выходах второй копии ИКС.
В случае неудачи этот процесс продолжается до тех пор, пока на выходе 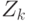 не появятся значения
не появятся значения  ,
, 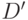 или же число копий
или же число копий  превысит максимально допустимое число копий ИКС. В последнем случае неисправность считается избыточной, т.е. непроверяемой (при данной постановке задачи). В случае успеха входные вектора копий ИКС
превысит максимально допустимое число копий ИКС. В последнем случае неисправность считается избыточной, т.е. непроверяемой (при данной постановке задачи). В случае успеха входные вектора копий ИКС 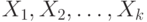 образуют искомую проверяющую последовательность.
Следует отметить, что на практике значительная часть последовательностных ЦУ для большинства переменных состояний имеет специальные цепи сброса и это можно использовать при построении теста, установив переменные состояния
образуют искомую проверяющую последовательность.
Следует отметить, что на практике значительная часть последовательностных ЦУ для большинства переменных состояний имеет специальные цепи сброса и это можно использовать при построении теста, установив переменные состояния 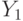 в соответствующие значения. При прямом подходе эту информацию использовать значительно легче (и естественнее, поскольку это ведет к значительному снятию неопределенности в схеме).
в соответствующие значения. При прямом подходе эту информацию использовать значительно легче (и естественнее, поскольку это ведет к значительному снятию неопределенности в схеме).
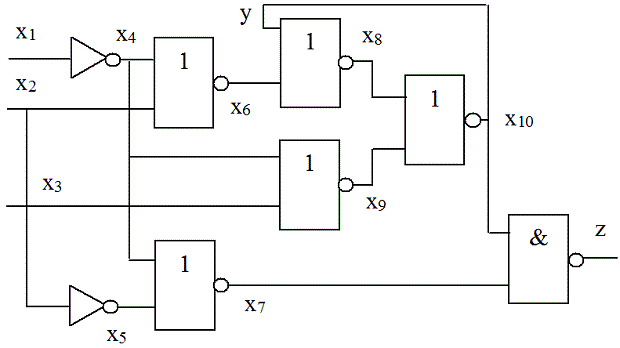
Суть метода рассмотрим на примере схемы, приведенной на рис. 23.7. Прежде всего, необходимо выполнить условный обрыв обратных связей и получить комбинационный эквивалент (рис. 23.8). Допустим, что требуется построить тест для константной неисправности 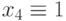 .
Структурная импликация для нашего примера дает
.
Структурная импликация для нашего примера дает  .
Затем внесем влияние неисправности, положив
.
Затем внесем влияние неисправности, положив  . Попытаемся распространить значения
. Попытаемся распространить значения 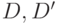 до выхода
до выхода 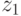 (при
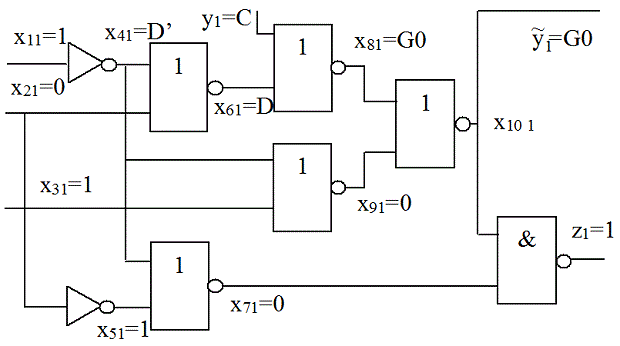
(при  ) сначала для схемы из одного КЭ (рис. 23.8).
Можно убедиться, что для данной неисправности это невозможно сделать. Но для псевдовыхода
) сначала для схемы из одного КЭ (рис. 23.8).
Можно убедиться, что для данной неисправности это невозможно сделать. Но для псевдовыхода 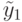 , как показано на рис. 23.8, можно снизить неопределенность до
, как показано на рис. 23.8, можно снизить неопределенность до 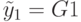 с помощью присваивания входам следующих значений:
с помощью присваивания входам следующих значений: 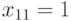 ,
, 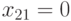 ,
, 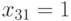 .
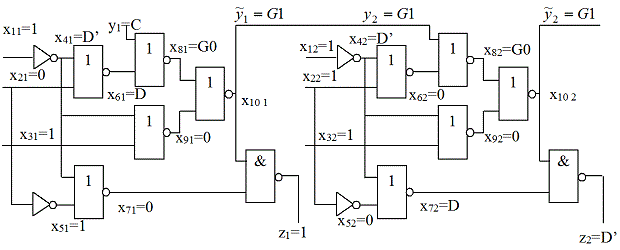
Затем наращиваем итеративную схему путем дополнения ее второй копией комбинационного эквивалента (рис. 23.9). Вносим влияние неисправности во вторую копию, полагая
.
Затем наращиваем итеративную схему путем дополнения ее второй копией комбинационного эквивалента (рис. 23.9). Вносим влияние неисправности во вторую копию, полагая  , и имеем теперь неисправность с кратностью
, и имеем теперь неисправность с кратностью  . Попытаемся распространить значения
. Попытаемся распространить значения 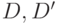 к выходу
к выходу 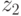 .
На этот раз это удается сделать с помощью значений входов второй копии:
.
На этот раз это удается сделать с помощью значений входов второй копии: 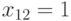 ,
, 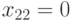 ,
, 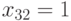 . Таким образом, получаем проверяющую последовательность
. Таким образом, получаем проверяющую последовательность
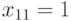 ,
, 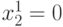 ,
, 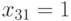 ;
; 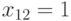 ,
, 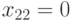 ,
, 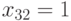 длиной в два набора для данной неисправности.
длиной в два набора для данной неисправности.