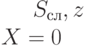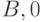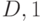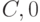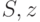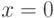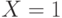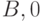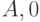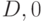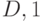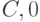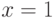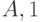Построение тестов для устройств с памятью на основе экспериментов с автоматами

22.2 Идентифицирующие последовательности конечных автоматов

В основе построения контрольного эксперимента или теста лежит построение диагностической последовательности (ДП) [22.6]. В случае, когда ДП не может быть построена, применяются модифицированные проверяющие эксперименты [22.7], основанные на использовании уникальной последовательности. Также при построении проверяющих экспериментов применяются синхронизирующая и установочная последовательности [22.5]. Данные последовательности определяются одним общим термином идентифицирующие последовательности.

Определение 22.5 Установочной называется входная последовательность, которая однозначно идентифицирует конечное состояние КА по его выходной реакции независимо от начального состояния.

Таблица 22.3.

Таблица 22.4.

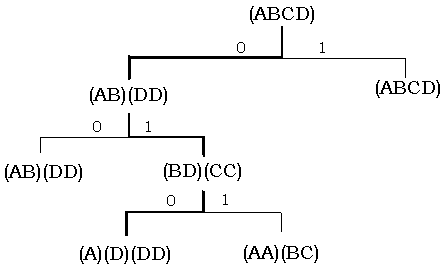
Рис. 22.4. Фрагмент ПРД для КА, заданного таблицей 22.3, строящего установочную последовательность (010).

Рассмотрим построение установочной последовательности для КА с помощью ПРД на примере. Пусть имеется КА, заданный таблицей 22.3. ПРД для данного КА имеет вид, приведенный на рис. 22.4. Из него видно, что установочной последовательностью для рассматриваемого КА является входная последовательность . табл. 22.4, в которой приведены выходные состояния и реакции автомата (табл. 22.3) на входную последовательность , экспериментально подтверждает полученный результат. Из нее видно, что конечные состояния и однозначно идентифицируются этой входной последовательностью.

Определение 22.6 Диагностической называется входная последовательность, для которой выходные реакции КА различаются для каждого начального состояния.

Таблица 22.5.

Таблица 22.6.

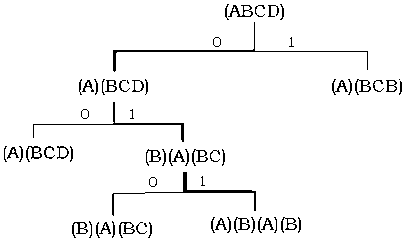
Рис. 22.5. Фрагмент ПРД для КА, заданного таблицей 22.5, строящего диагностическую последовательность (011).

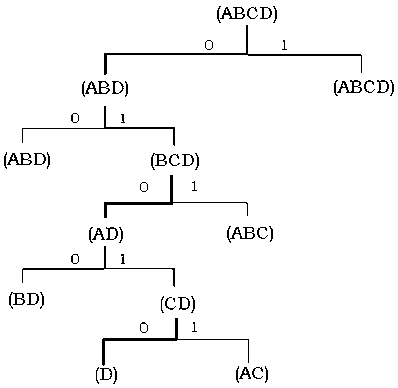
Рис. 22.6. Фрагмент ДПС+, строящего синхронизирующую последовательность T=(01010) (жирная линия) для конечного состояния D.

Из определения следует, что диагностическая последовательность позволяет определить начальное состояние автомата, исходя из выходной реакции КА. Рассмотрим построение диагностической последовательности для КА с помощью ПРД на примере КА, заданного таблицей 22.5. Из вида ПРД для данного КА (рис. 22.5) видно, что диагностической последовательностью для рассматриваемого КА является входная последовательность . табл. 22.6 выходных состояний и реакций данного автомата на входную последовательность , экспериментально подтверждает полученный результат. Из нее видно, что все начальные состояния однозначно идентифицируются этой входной последовательностью, т.е. имеют различные выходные последовательности.

Определение 22.7 Синхронизирующей называется входная последовательность, которая переводит КА в определенное конечное состояние независимо от его начального состояния.

Синхронизирующая последовательность строится на основе ДПС+ данного КА, но без учёта выходных реакций. Синхронизирующую последовательность имеют далеко не все автоматы. Например, на рис. 22.6 приводится фрагмент ДПС+, с помощью которого строится синхронизирующая последовательность (путь от вершины дерева выделен жирной линией) для конечного состояния .