|
Добрый день можно поинтересоваться где брать литературу предложенную в курсе ?Большинство книг я не могу найти в известных источниках |
Методы генерации тестов PODEM, FAN и SOCRATES
19.2 Метод FAN
Идеи, заложенные в этом методе, получили развитие в алгоритме "FAN" (fan-out oriented test generation)[19.2]. В нем предусмотрена препроцессорная обработка, в которой анализируется структура ДУ, которая разбивается на древовидные подсхемы. Метод использует следующие стратегии.
- На каждом шаге алгоритма определяется, насколько это возможно, множество сигналов, которые получают определенные значения вследствие импликации. В отличие от предыдущего метода, здесь используется как прямая, так и обратная импликация.
- Присваиваются значения
 ,
, 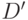 , которые однозначно определяются неисправностью.
, которые однозначно определяются неисправностью.
- В том случае, когда
 -граница состоит из одного элемента, используется одномерная активизация.
-граница состоит из одного элемента, используется одномерная активизация.
- Более эффективная процедура кратного продвижения назад (по нескольким путям).
- Продвижение назад останавливается, если в узлах разветвления возникают противоречия (конфликт).
Более эффективные процедуры продвижения назад и перебора позволяют уменьшить количество возвратов при поиске теста и тем самым уменьшить время генерации теста.
Выполнение импликации в обоих направлениях позволяет в некоторых случаях раньше обнаруживать конфликтные ситуации и, что еще более важно избыточные неисправности. Отметим, что многие алгоритмы генерации тестов тратят большие вычислительные ресурсы на избыточные неисправности (для которых нельзя построить тестовый набор). Поскольку задача построения теста носит переборный характер, то в худшем случае потребуется рассмотреть всевозможные значения входных переменных. Если схема имеет достаточно много избыточных неисправностей, то система генерации тестов может более половины времени работать на построение тестов, которые не существуют. Поэтому избыточные неисправности желательно находить как можно быстрее.
Процедура кратного продвижения назад по нескольким путям позволяет методу FAN по сравнению с PODEM быстрее обнаруживать конфликтные ситуации в процессе построения тестов и тем самым сократить число возвратов при переборе. Напомним, что процедура продвижения назад в PODEM при прохождении каждого логического элемента выбирает только один его вход и определяет значение для него, что фактически способствует увеличению перебираемых вариантов. Особенно это заметно для ситуаций с выбором "тяжелых подзадач". Например, для обеспечения значения 1 выхода вентиля И необходимо, чтобы все его входы получили также значения 1.Но метод PODEM выберет и присвоит значение только одному (самому "тяжелому" входу) и распространит его назад ко входам схемы. Для остальных входов выполняется своя процедура продвижения назад. В методе FAN в такой ситуации всем входам присваиваются значения 1, которые далее распространяются ко входам схемы одновременно. Это тоже способствует более раннему обнаружению конфликтов при генерации теста.
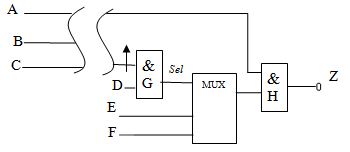
В том случае, когда  -граница содержит один элемент, в методе FAN применяется одномерная активизация. Рассмотрим схему рис. 19.6 [19.3],
-граница содержит один элемент, в методе FAN применяется одномерная активизация. Рассмотрим схему рис. 19.6 [19.3],
для которой необходимо построить тест для неисправности coinst1 входа вентиля G. Влияние неисправности должно распространяться через мультиплексор и вентиль H. Для распространения через вентиль H его верхнему входу необходимо присвоить значение 1. Но из процедуры активизации в месте неисправности следует, что этот вход устанавливается в блокирующее значение 0. Поэтому для обнаружения подобных ситуаций в методе FAN выполняется одномерная активизация. Для нашего примера при активизации необходимо установить значение верхнего входа 1. Оно при импликации дает конфликт в месте неисправности.
На этапе препроцессорной обработки схема разбивается на одновыходные древовидные подсхемы, которые не содержат сходящихся разветвлений. Очевидно, внутри таких подсхем продвижение назад выполняется без конфликтов и может остановиться на линиях, которые являются выходами предыдущих подсхем без разветвлений. После того, как в процессе продвижения назад внутри подсхемы некоторые линии получили определенно значение, можно выполнить процедуру подтверждения этих значений.
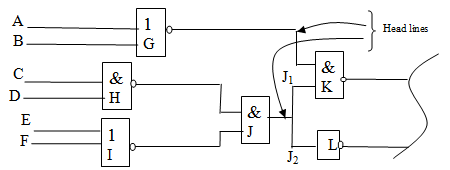
Рассмотрим узел разветвления 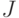 на рис. 19.7 [19.3] c ветвями
на рис. 19.7 [19.3] c ветвями 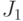 и
и 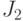 .
.
Здесь вентили  и
и 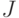 являются выходами древовидных подсхем (иногда их называют головными - head). Если существует путь от узла разветвления вперед (по направлению к выходам) до схемы
являются выходами древовидных подсхем (иногда их называют головными - head). Если существует путь от узла разветвления вперед (по направлению к выходам) до схемы  , то схема называется граничной (bound). Схемы, которые не являются граничными, называются свободными.
Для нашего примера схемы
, то схема называется граничной (bound). Схемы, которые не являются граничными, называются свободными.
Для нашего примера схемы 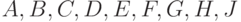 являются граничными, в то время как схемы
являются граничными, в то время как схемы 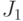 ,
, 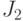 ,
,  и
и  представляют свободные схемы. Свободные схемы, которые непосредственно питают граничные cхемы (как в случае разветвления
представляют свободные схемы. Свободные схемы, которые непосредственно питают граничные cхемы (как в случае разветвления 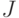 ) или через логические элементы (случай
) или через логические элементы (случай  ) являются головными (head). Они определяют границу между свободными и граничными линиями.
) являются головными (head). Они определяют границу между свободными и граничными линиями.
Как и предыдущий метод FAN работает на каждом шаге на достижение поставленных целей. Это логические значения некоторых линий схемы, которые должны быть обеспечены в течение поиска теста. Процедура продвижения назад начинается с начальных целей. На начальном этапе эти цели обусловлены значениями  или
или 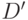 на неисправных линиях, которые определяются при инициализации неисправностей.
Начальные цели становятся текущими при входе в процедуру кратного продвижения назад Mback. В процессе выполнения этой процедуры некоторые линии схемы получают новые значения, которые могут стать новыми текущими целями или головными (head) целями или целями узлов разветвления (FPO), которые в конечном счете должны быть выполнены.Здесь цели соответствующие головным (head) линиям, называются головными. Аналогично определяются цели соответствующие узлам разветвления FPO. При выполнении текущих целей в процессе продвижения назад FAN останавливается на узлах разветвлениях и головных линиях до тех пор, пока не выполнены текущие цели.
Затем выбирается узел разветвления, ближайший к внешнему выходу, если такой существует. Головные (head) цели всегда выполняются последними, после того, как достигнуты остальные цели, которые вследствие отсутствия разветвлений могут быть выполнены без конфликтов.
Если на узле разветвления возникает конфликтная ситуация, то она должна быть разрешена. Конфликт случается в том случае, когда при выполнении процедуры кратного продвижения назад два или более путей сходятся на узле разветвления с противоположными требованиями (0 и 1). Если на узле разветвления нет конфликта, то процедура кратного продвижения назад Mback проходит этот узел и продолжает продвижение назад внутри другой древовидной подсхемы.
на неисправных линиях, которые определяются при инициализации неисправностей.
Начальные цели становятся текущими при входе в процедуру кратного продвижения назад Mback. В процессе выполнения этой процедуры некоторые линии схемы получают новые значения, которые могут стать новыми текущими целями или головными (head) целями или целями узлов разветвления (FPO), которые в конечном счете должны быть выполнены.Здесь цели соответствующие головным (head) линиям, называются головными. Аналогично определяются цели соответствующие узлам разветвления FPO. При выполнении текущих целей в процессе продвижения назад FAN останавливается на узлах разветвлениях и головных линиях до тех пор, пока не выполнены текущие цели.
Затем выбирается узел разветвления, ближайший к внешнему выходу, если такой существует. Головные (head) цели всегда выполняются последними, после того, как достигнуты остальные цели, которые вследствие отсутствия разветвлений могут быть выполнены без конфликтов.
Если на узле разветвления возникает конфликтная ситуация, то она должна быть разрешена. Конфликт случается в том случае, когда при выполнении процедуры кратного продвижения назад два или более путей сходятся на узле разветвления с противоположными требованиями (0 и 1). Если на узле разветвления нет конфликта, то процедура кратного продвижения назад Mback проходит этот узел и продолжает продвижение назад внутри другой древовидной подсхемы.
Для того, чтобы сохранить полученные значения в процессе продвижения назад и разрешить конфликтные ситуации, FAN использует запись целей в виде триплета  ). Здесь
). Здесь  означает целевую схему,
означает целевую схему, 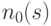 представляет число нулей, которые потребовалось установить при продвижении до
представляет число нулей, которые потребовалось установить при продвижении до  , и
, и  - соответственно число требуемых единиц. При этой терминологии конфликт возникает, если оба числа
- соответственно число требуемых единиц. При этой терминологии конфликт возникает, если оба числа 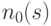 и
и  имеют ненулевые значения. Для разрешения конфликта используется правило: если
имеют ненулевые значения. Для разрешения конфликта используется правило: если 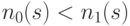 , то узлу разветвления приписывается 1, в противном случае - 0.
, то узлу разветвления приписывается 1, в противном случае - 0.
При продвижении назад через логический элемент логические значения его входов зависят от значения на выходе и типа вентиля. Для И/НЕ-И вентилей 1/0 на выходе ведет к присвоению 1 на всех его входах. Соответственно для вентилей ИЛИ/НЕ-ИЛИ 0/1 на выходе ведет к необходимости присвоения значений 0 всем его входам. Кроме этого, если вентиль инвертирующего типа, то значения 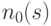 и
и  в триплете меняются местами. Например, для вентиля НЕ-ИЛИ с триплетом
в триплете меняются местами. Например, для вентиля НЕ-ИЛИ с триплетом 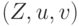 на выходе его входам присваивается триплет
на выходе его входам присваивается триплет 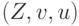 , если значение 1 требуется на выходе.
, если значение 1 требуется на выходе.
Если входу вентиля необходимо присвоить контролирующее значение (0 для И или НЕ-И, 1 для ИЛИ или НЕ-ИЛИ), то при продвижении назад через логический элемент выбирается как и в методе PODEM выбирается вход, имеющий лучшую управляемость. Предположим, что вентиль имеет входы 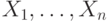 и выход
и выход  и без потери общности вход
и без потери общности вход 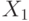 имеет лучший показатель управляемости.
Тогда при продвижении назад через логический элемент значения
имеет лучший показатель управляемости.
Тогда при продвижении назад через логический элемент значения 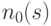 ,
,  для его входов можно найти (по заданным значения выхода
для его входов можно найти (по заданным значения выхода 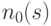 ,
,  ) согласно правилам, приведенным в табл. 19.2 [19.3].
) согласно правилам, приведенным в табл. 19.2 [19.3].
| N п/п | Функция | 0-счетчик | 1-счетчик | Управляемость |
|---|---|---|---|---|
| 1 | И |
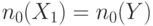
|
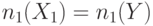
|
легкий 0 |
| 2 | И |
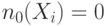
|
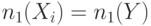
|
остальные |
| 3 | НЕ-И |
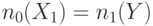
|
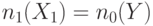
|
легкий 0 |
| 4 | НЕ-И |
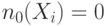
|
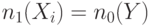
|
остальные |
| 5 | ИЛИ |
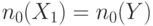
|
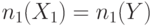
|
Легкая 1 |
| 6 | ИЛИ |
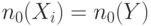
|
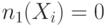
|
остальные |
| 7 | НЕ-ИЛИ |
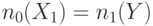
|
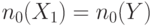
|
Легкая 1 |
| 8 | НЕ-ИЛИ |
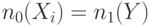
|
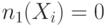
|
остальные |
| 9 | НЕ |
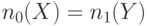
|

|
|
| 10 | разветвление |

|

|
Рассмотрим для примера распространение назад триплета через вентиль И. Если на выходе этого вентиля необходимо установить 0, то очевидно хотя бы один из его входов надо установить в 0. В методе FAN выбирается "легкий вход" с лучшим показателем управляемости за исключением тех входов, которые уже выбирались и были отвергнуты вследствие возникновения конфликта. Согласно первой строке табл. 19.2 значения 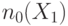 и
и 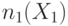 для выбранного входа приравниваются соответствующим значениям выхода элемента:
для выбранного входа приравниваются соответствующим значениям выхода элемента: 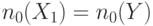 ,
, 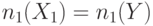 .
С другой стороны для неконтролирующих значений (1) имеем
.
С другой стороны для неконтролирующих значений (1) имеем 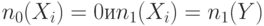 , что представлено во второй строке табл. 19.2. Третья строка таблицы показывает, что при наличии инверсии значения
, что представлено во второй строке табл. 19.2. Третья строка таблицы показывает, что при наличии инверсии значения 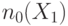 и
и 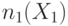 меняются местами, то есть
меняются местами, то есть 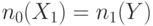 ,
, 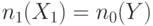 . Аналогичный смысл имеют остальные правила, приведенные в табл. 19.2. Особо следует отметить распространение через узел разветвления, где согласно последней строке табл. 19.2. значения
. Аналогичный смысл имеют остальные правила, приведенные в табл. 19.2. Особо следует отметить распространение через узел разветвления, где согласно последней строке табл. 19.2. значения 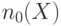 и
и 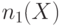 суммируются.
суммируются.
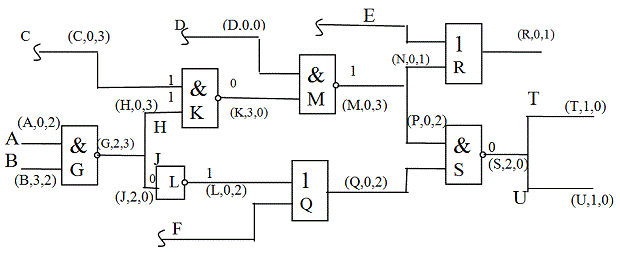
Применение этих правил рассмотрим на примере схемы 19.8 [19.3].
Предположим, что в процессе обратного распространения на ветвях разветвления получились значения  и
и 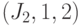 . Поскольку оба значения
. Поскольку оба значения 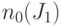 и
и 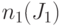 для ветви
для ветви 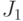 ненулевые (как и для второй ветви
ненулевые (как и для второй ветви 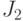 ), то имеет место конфликтная ситуация - не ясно, какое значение надо присвоить для разветвления
), то имеет место конфликтная ситуация - не ясно, какое значение надо присвоить для разветвления 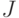 .
Поскольку нулевое значение имеет вес 2, а единичное - вес 3, то мы выбираем для
.
Поскольку нулевое значение имеет вес 2, а единичное - вес 3, то мы выбираем для 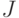 значение 1 с большим весом. Так как сложилась конфликтная ситуация, то кратное продвижение назад в этом месте прекращается и необходимо разрешить конфликт путем возврата к точке последнего выбора и присвоения альтернативного значения. Если на узле разветвления невозможно найти согласованные значения, то неисправность является избыточной.
значение 1 с большим весом. Так как сложилась конфликтная ситуация, то кратное продвижение назад в этом месте прекращается и необходимо разрешить конфликт путем возврата к точке последнего выбора и присвоения альтернативного значения. Если на узле разветвления невозможно найти согласованные значения, то неисправность является избыточной.