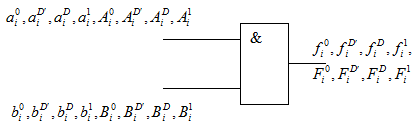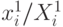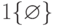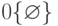|
Добрый день можно поинтересоваться где брать литературу предложенную в курсе ?Большинство книг я не могу найти в известных источниках |
Дедуктивный метод моделирования неисправностей
12.2 Дедуктивное моделирование в троичном алфавите
Распространение дедуктивного метода моделирования на троичный алфавит можно реализовать несколькими способами [12.4]. Рассмотрим один из них. При этом каждой  -ой линии схемы ставятся в соответствие двоичные переменные
-ой линии схемы ставятся в соответствие двоичные переменные 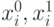 и два списка неисправностей
и два списка неисправностей 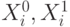 .
Правила обработки списков неисправностей зависят от логической функции элемента и применяемого способа кодирования алфавита. Как и для параллельного метода , в троичном алфавите, мы будем использовать дизъюнктивный метод кодирования, представленный табл. 11.2. При этом, как уже говорилось, фактически моделирование каждого вентиля в троичном алфавите заменяется моделированием двух вентилей в двоичном алфавите (рис. 5.4). Но схему в двоичном алфавите мы уже умеем моделировать дедуктивным методом. Поэтому для каждого из этих двух вентилей можно применять приведенные выше правила распространения неисправностей (в двоичном алфавите), что решает проблему обобщения дедуктивного моделирования на троичный алфавит. На рис. 12.3 это представлено в графическом виде. Так, например, для
.
Правила обработки списков неисправностей зависят от логической функции элемента и применяемого способа кодирования алфавита. Как и для параллельного метода , в троичном алфавите, мы будем использовать дизъюнктивный метод кодирования, представленный табл. 11.2. При этом, как уже говорилось, фактически моделирование каждого вентиля в троичном алфавите заменяется моделированием двух вентилей в двоичном алфавите (рис. 5.4). Но схему в двоичном алфавите мы уже умеем моделировать дедуктивным методом. Поэтому для каждого из этих двух вентилей можно применять приведенные выше правила распространения неисправностей (в двоичном алфавите), что решает проблему обобщения дедуктивного моделирования на троичный алфавит. На рис. 12.3 это представлено в графическом виде. Так, например, для  получаем в соответствии с дизъюнктивным кодированием
получаем в соответствии с дизъюнктивным кодированием 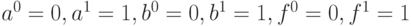 (показано на рис. 12.3) следующие правила распространения:
(показано на рис. 12.3) следующие правила распространения:

Здесь 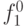 означает неисправность константа 1 нулевой компоненты троичного алфавита переменной
означает неисправность константа 1 нулевой компоненты троичного алфавита переменной  , и
, и 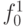 - константа 0 единичной компоненты.
- константа 0 единичной компоненты.
12.3 Дедуктивное моделирование в многозначных алфавитах
Как указывалось ранее, основной проблемой при дедуктивном методе моделирования в многозначных алфавитах является построение моделей логических элементов в виде теоретико-множественных операций над списками неисправностей. Такие модели должны позволять находить выходные списки неисправностей по заданным входным спискам. В настоящем разделе на базе универсальной модели логических элементов в многозначных алфавитах раздела 3 предложен метод построения моделей для дедуктивного моделирования неисправностей в многозначных алфавитах.
При дедуктивном методе моделирования в многозначном алфавите, например 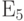 , каждой линии
, каждой линии  ДУ поставим в соответствие четыре переменные
ДУ поставим в соответствие четыре переменные 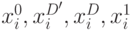 ,
принимающие двоичные значения
,
принимающие двоичные значения 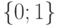 и четыре списка неисправностей
и четыре списка неисправностей
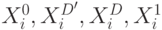 , связанные с этими переменными. Например, на рис. 12.4 представлены соответствующие списки неисправностей и покомпонентные переменные для вентиля
, связанные с этими переменными. Например, на рис. 12.4 представлены соответствующие списки неисправностей и покомпонентные переменные для вентиля
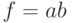 .
.
Ключевым вопросом является распространение списков неисправностей через логический элемент (для нашего примера по заданным спискам 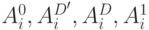 и
и 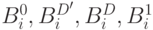 определение списков
определение списков 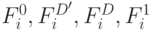 ).
Суть предлагаемого метода заключается в том, что каждой из двоичной компонент ставится в соответствие список неисправностей, изменяющих значение этой компоненты на противоположное, а теоретико-множественные операции
).
Суть предлагаемого метода заключается в том, что каждой из двоичной компонент ставится в соответствие список неисправностей, изменяющих значение этой компоненты на противоположное, а теоретико-множественные операции 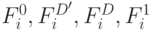 для распространения входных списков неисправностей выводятся из булевых функций
для распространения входных списков неисправностей выводятся из булевых функций 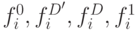 .
.
Рассмотрим неисправность  , при которой в исправном ДУ
, при которой в исправном ДУ 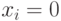 , а в неисправном
, а в неисправном 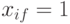 . Тогда неисправность
. Тогда неисправность  может быть представлена следующим образом:
может быть представлена следующим образом:
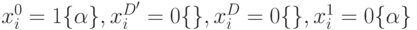 .
Эта нотация означает, что неисправность
.
Эта нотация означает, что неисправность  входит в списки неисправностей
входит в списки неисправностей
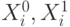 и не входит в списки
и не входит в списки  . Поскольку в исправном ДУ
. Поскольку в исправном ДУ 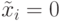 , что соответствует
, что соответствует
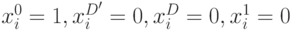 согласно кодированию табл. 12.1, и неисправность
согласно кодированию табл. 12.1, и неисправность  меняет значения компонент
меняет значения компонент
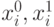 на противоположное, так как она входит списки
на противоположное, так как она входит списки 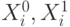 , получаем значения
, получаем значения
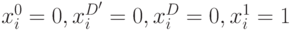 , которые являются кодом
, которые являются кодом 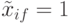 .
Аналогично неисправность
.
Аналогично неисправность  ,
при которой
,
при которой 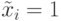 и
и 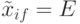 представляется
представляется
 .
В табл. 11.1 приведены всевозможные комбинации значений
.
В табл. 11.1 приведены всевозможные комбинации значений
 и
и
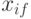 (в исправном и неисправном ДУ) и их представления в указанной нотации. Теоретико-множественные операции над входными списками для получения выходных списков
(в исправном и неисправном ДУ) и их представления в указанной нотации. Теоретико-множественные операции над входными списками для получения выходных списков
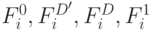 выводятся из функций
выводятся из функций
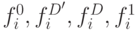 .
.
Поскольку это "обычные" булевы функции, то для этих операций можно использовать известные методы, например, изложенные в [12.4,12.5]. Как правило, указанные методы ориентированы на вывод теоретико-множественных операций для определенных входных наборов двоичных значений данной булевой функции.
Рассмотрим распространение входных списков неисправностей в пятизначном алфавите 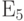 на примере вентиля
на примере вентиля 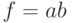 . Его поведение в алфавите
. Его поведение в алфавите 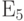 описывается следующими компонентами:
описывается следующими компонентами:
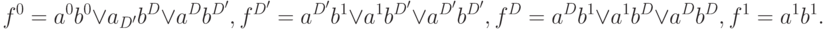
Пусть на входах вентиля имеются следующие значения сигналов и списки неисправностей:

Результаты показывают, что в исправном ДУ 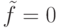 , а при неисправности
, а при неисправности  имеет место
имеет место 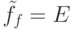 . Аналогично при неисправностях
. Аналогично при неисправностях 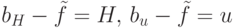 . Таким образом, неисправности
. Таким образом, неисправности
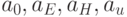 на выходе вентиля не проявляются, а неисправности
на выходе вентиля не проявляются, а неисправности
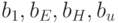 распространяются на его выход. Если во множество моделируемых неисправностей входят const0 и const1 на выходе вентиля, то мы должны добавить неисправность
распространяются на его выход. Если во множество моделируемых неисправностей входят const0 и const1 на выходе вентиля, то мы должны добавить неисправность 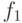 в списки (
в списки (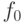 не проверяется). В результате получим
не проверяется). В результате получим

Основным преимуществом предлагаемого подхода является то, что при разработке моделей цифровых микросхем (правил распространения входных списков неисправностей) не нужно строить новые модели, а можно использовать универсальные модели для многозначных алфавитов, предложенные в "Система многозначных алфавитов и функций" . Поскольку разработаны формальные методы построения моделей, вывод их может быть автоматизирован. Данные модели по сложности не превосходят предложенные в работах [12.4,12.5].
Ключевые термины:
Список неисправностей - связывается с линией схемы и включает в себя множество неисправностей, изменяющих значение сигнала на линии на противоположное.
Правила распространения неисправностей - определяются для логического элемента и его текущих входных значений сигнала; позволяют определить список неисправностей, связанный с выходом элемента, по заданным входным спискам неисправностей.
Троичный алфавит - включаетсимволы  , где символ
, где символ  соответствует неопределенному значению сигнала.
соответствует неопределенному значению сигнала.
Многозначный алфавит - включает много (больше 3) символов, отражающих различные распределения сигналов в схеме.
Краткие итоги
Рассмотрен дедуктивный метод моделирования неисправностей, который основан на обработке списков неисправностей, связанных с каждой линией схемы.
В "Дедуктивный метод моделирования неисправностей " приведено определение списка неисправности для линии схемы, включающего все одиночные константные неисправности замыкания, которые дают на данной линии значения сигналов, противоположные значениям в исправной схеме.
"Последовательное и параллельное моделирование неисправностей" посвящен распространению дедуктивного метода на троичный алфавит. В этом случае используется дизъюнктивное кодирование троичного алфавита и с каждой линией связывается два списка неисправностей. Это позволяет свести троичное моделирование к двоичному и использовать стандартную технику дедуктивного метода.
В "Неконстантные неисправности" изложено распространение дедуктивного метода на многозначный алфавит, В этом случае с каждой линией связывается четыре списка неисправностей и исползуется двоичное кодирование многозначного алфавита.
Вопросы и упражнения
- Определите список неисправностей, используемый в дедуктивном методе.
- Выведите правило распространения неисправностей для элемента
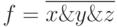 при
при 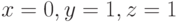 .
.
- Выведите правило распространения неисправностей для элемента
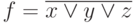 при
при 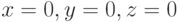 .
.
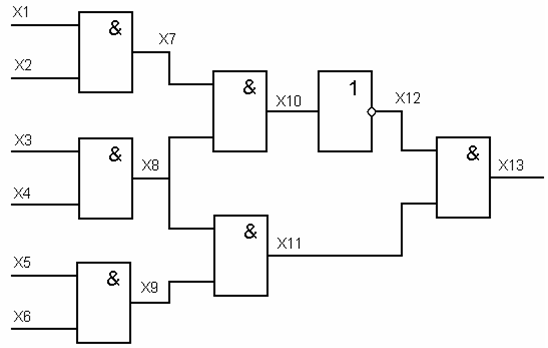
- Выполните дедуктивное моделирование в двоичном алфавите для всех одиночных константных неисправностей приведенной схемы рис. 12.5 на тестовом наборе (111111).
- Как распространяется дедуктивный метод на троичный алфавит?
- Сколько и каких списков неисправностей связывается при этом с каждой линией схемы?
- Как увеличиваются при этом затраты памяти и быстродействие?
- Как распространяется дедуктивный метод на многозначный алфавит?
- Какой метод кодирования многозначных сигналов используется при этом?
- Сколько и каких списков неисправностей связывается при этом с каждой линией схемы?
- Как выполняется распространение неисправностей в многозначном алфавите?.