|
Добрый день можно поинтересоваться где брать литературу предложенную в курсе ?Большинство книг я не могу найти в известных источниках |
Машинные модели логических схем и управление процессом моделирования
Управление процессом моделирования
Как уже отмечалось, во многих случаях алгоритм моделирования можно представить следующим образом. После подачи входного воздействия на модель ДУ поочерёдно вычисляются значения на выходах всех элементов по значениям на их входах. Такая процедура называется итерацией. В результате вычислений значения некоторых сигналов могут измениться. В этом случае необходимо выполнить вторую итерацию (т.е. вычислить значения на выходах всех элементов по новым значениям на их входах), затем третью итерацию и так далее до тех пор, пока все сигналы не примут установившиеся значения. В этом случае процесс моделирования (на одном входном наборе) сходится естественным образом. Возможен и другой результат моделирования – значения сигналов на некоторых линиях периодически изменяются. В этом случае говорят, что моделирование не сходится из-за генерации модели ДУ. Такая ситуация может быть, например, в ДУ, содержащем контур обратной связи с нечетным числом инверсий.
Поэтому для сходимости процесса необходимо иметь критерий окончания моделирования. Обычно задают два критерия: совпадение результатов моделирования на соседних
итерациях или достижение некоторого предельного числа итераций  .
.
Событийное моделирование

Как отмечалось выше, в зависимости от очередности обработки логических элементов различают сквозные и событийные методы логического моделирования. При сквозном методе на каждой итерации каждый логический элемент моделируется заново вне зависимости от того, произошли изменения сигналов на его входах или нет. В событийном методе логический элемент моделируется только в том случае, если на его входах произошло событие – изменилось значение сигнала хотя бы на одном из его входов. Для элементов памяти событием является также изменение его состояния (изменение переменной внутреннего состояния). Обычно в процессе моделирования на каждой итерации активны (имеют изменения на входах) только несколько процентов элементов (3-5%), поэтому событийный метод гораздо быстрее сквозного.
В дальнейшем мы будем, в основном, рассматривать событийные интерпретативные методы логического моделирования. При этом будет использоваться, как правило, модель номинальной задержки, при которой каждому логическому элементу присваивается своя целочисленная задержка в некоторых условных единицах, определяемых масштабом модельного времени. Следует отметить, что события происходят в определенные моменты времени, поэтому необходим механизм моделирования временной очередности событий. В приведенном выше листинге "Событийное моделирование" представлен укрупненный алгоритм событийного интерпретативного логического моделирования [ 1.2 ] .
При этом центральное место занимает понятие очереди будущих событий (ОБС)
[
2.3
]
,
[
2.7
]
. Каждое событие в ОБС содержит номер элемента  и соответствующее значение сигнала
и соответствующее значение сигнала
 . Это событие при моделировании привязывается в соответствии с задержкой
. Это событие при моделировании привязывается в соответствии с задержкой  выхода
выхода  элемента к моменту времени
элемента к моменту времени
 , где
, где  — текущее модельное время. Значения сигналов при этом для текущего момента времени хранятся в массиве
— текущее модельное время. Значения сигналов при этом для текущего момента времени хранятся в массиве  .
Вновь вычисленные значения элементов записываются в ОБС с учетом задержки
.
Вновь вычисленные значения элементов записываются в ОБС с учетом задержки  .
.
Для упорядочения событий в ОБС используют различные способы моделирования временного механизма. Один из них использует при программной реализации структуру связанных списков, как это показано на рис.5.2 .
Здесь каждому моменту времени соответствует свой список ОБС. Времена  упорядочены и связаны списком. Занесение нового события с
использованием этого способа требуют поиска нужного
упорядочены и связаны списком. Занесение нового события с
использованием этого способа требуют поиска нужного 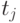 путём просмотра соответствующих указателей. Если моменты времени, для которых ОБС не пусты,
идут достаточно плотно, то эффективней другой способ моделирования временного механизма, который показан на рис.5.3 .
путём просмотра соответствующих указателей. Если моменты времени, для которых ОБС не пусты,
идут достаточно плотно, то эффективней другой способ моделирования временного механизма, который показан на рис.5.3 .
При этом для хранения указателей ОБС используется массив,
"завязанный в кольцо". Каждый элемент массива соответствует моменту модельного времени. Включение нового элемента при этом не требует поиска. Так, например,
если в текущий момент времени  моделируется элемент
моделируется элемент  , имеющий задержку
, имеющий задержку 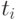 , то событие
, то событие  нужно занести в
ОБС, для которого указатель содержится в элементе массива
нужно занести в
ОБС, для которого указатель содержится в элементе массива  . С другой стороны этот способ не эффективен, если интервалы времени между событиями
достаточно велики. Элементы массива при этом будут иметь в основном нулевые указатели, а сам массив может иметь чрезмерно большой размер. Наличие временного
механизма позволяет при моделировании подавать тестовые наборы через соответствующие интервалы модельного времени. Для этого перед началом моделирования все изменения
входных воздействий заносятся в ОБС, соответствующие временам изменения. Поэтому в процессе моделирования изменения входов обрабатываются наравне с другими событиями и в
процессе моделирования нет необходимости ждать, пока значения сигналов стабилизируются на всех линиях.
. С другой стороны этот способ не эффективен, если интервалы времени между событиями
достаточно велики. Элементы массива при этом будут иметь в основном нулевые указатели, а сам массив может иметь чрезмерно большой размер. Наличие временного
механизма позволяет при моделировании подавать тестовые наборы через соответствующие интервалы модельного времени. Для этого перед началом моделирования все изменения
входных воздействий заносятся в ОБС, соответствующие временам изменения. Поэтому в процессе моделирования изменения входов обрабатываются наравне с другими событиями и в
процессе моделирования нет необходимости ждать, пока значения сигналов стабилизируются на всех линиях.
В листинге "Алгоритм логического моделирования" представлен укрупненный алгоритм логического моделирования на основе временного механизма в виде очереди будущих событий. Этот алгоритм отражает движение по очереди будущих событий.
В каждый (не пустой) момент времени события обрабатываются по алгоритму, представленному в листинге "Алгоритм логического моделирования" [44] (который реализует соответствующий шаг алгоритма рис.2.24).
Отметим, что представленный в листинге "Двухпроходной алгоритм обработки событий" алгоритм является двухпроходным. На первом проходе здесь переписываются события
 , связанные с моментом времени
, связанные с моментом времени  очереди будущих событий в буфер
– множество "Активные_элементы". Во время второго прохода выполняется собственно моделирование элементов
очереди будущих событий в буфер
– множество "Активные_элементы". Во время второго прохода выполняется собственно моделирование элементов  – последователей элемента
– последователей элемента
 и постановка в очередь будущих событий в соответствии с задержкой
и постановка в очередь будущих событий в соответствии с задержкой  элемента
элемента
 .
.
Алгоритм логического моделирования

Подобная (двухпроходная) стратегия позволяет в том случае, когда некоторый элемент  активизируется более одного раза, выполнять моделирование, вызванное
этим событием, только один раз. Следует отметить, что в приведенном алгоритме
активизируется более одного раза, выполнять моделирование, вызванное
этим событием, только один раз. Следует отметить, что в приведенном алгоритме  являются скорее кандидатами в события. Поэтому при обработке
множества "Активные_элементы" выполняется сравнение с текущим значением
являются скорее кандидатами в события. Поэтому при обработке
множества "Активные_элементы" выполняется сравнение с текущим значением  .
.
Двухпроходной алгоритм обработки событий

Улучшенный двухпроходной алгоритм обработки событий

В следующем алгоритме [ 2.3 ] , представленном выше, заносятся в ОБС только "истинные события", при которых происходит изменение сигнала. В [ 2.3 ] показано, что данный алгоритм является более эффективным. Преимущество двухпроходного алгоритма заключается в том, что он позволяет избежать повторных вычислений (моделирования одного и того же логического элемента) в случае наличия кратных событий, когда на входах имеет место изменение нескольких сигналов. Однако проведенный статистический анализ [ 2.3 ] показал, что кратные события в процессе моделирования случаются достаточно редко. Поэтому кроме двухпроходного были разработаны также однопроходные алгоритмы логического моделирования [ 2.3 ] . Один из таких алгоритмов [ 2.3 ] представлен в листинге "Однопроходной алгоритм обработки событий".
Несмотря на свою привлекательность (простоту и эффективность) этот алгоритм имеет недостаток. На рис.5.4 показана суть проблемы
обработки кратного события. Здесь на входе элемента  имеет место одновременное изменение двух сигналов
имеет место одновременное изменение двух сигналов  и
и  . Если эти события
обрабатываются в последовательности
. Если эти события
обрабатываются в последовательности  , то выход элемента
, то выход элемента  не изменяется и, следовательно, не ставится в
очередь будущих событий для последующей обработки.
не изменяется и, следовательно, не ставится в
очередь будущих событий для последующей обработки.
Однопроходной алгоритм обработки событий

Но если событие  обрабатывается первым, то результат
обрабатывается первым, то результат  будет поставлен в момент времени
будет поставлен в момент времени  очереди событий. Далее
обработка события
очереди событий. Далее
обработка события  вызывает событие
вызывает событие  , которое также будет отнесено к моменту времени
, которое также будет отнесено к моменту времени  . Таким образом, мы имеем
"импульс нулевой протяженности", что не соответствует реальному поведению схемы. Алгоритм, приведенный ниже, позволяет избежать подобных ситуаций.
. Таким образом, мы имеем
"импульс нулевой протяженности", что не соответствует реальному поведению схемы. Алгоритм, приведенный ниже, позволяет избежать подобных ситуаций.
Улучшенный однопроходной алгоритм обработки событий

Мы рассмотрели основные алгоритмы событийного логического моделирования с использованием модели номинальных задержек. Но они с небольшими изменениями могут быть использованы и для других более сложных моделей задержек, рассмотренных в "Модели логических элементов" (различные задержки для переднего и заднего фронтов, разброс задержек, инерционная задержка).
Ключевые термины:
Компилятивная модель схемы – представляется компьютерной программой, моделирующей данную схему.
Интерпретативная модель схемы – представляется системой связанных таблиц.
Событийное моделирование – здесь логический элемент моделируется в том случае, если на его входах произошло событие – изменение значений сигналов.
Очередь будущих событий – упорядоченные в модельном времени события (изменения сигналов на линиях схемы).
Краткие итоги
В лекции рассмотрены машинные модели цифровых схем и управление процессом логического моделирования..
В разделе 5.1 описаны машинные модели схем, которые используются в логическом моделировании, к которым относятся:
- компилятивная модель, изложенная в разделе 5.1.1;
- интерпретативная модель в виде связанных таблиц, которая представлена в 5.12.
В разделе 5.2 изложены основные алгоритмы логического событийного моделирования на основе очереди будущих событий, к которым относятся однопроходной и двухпроходной алгоритм обработки событий.
Вопросы и упражнения
- Какие используются машинные модели схемы?
- Опишите компилятивную модель схемы.
- Что составляет интерпретативную модель схемы.
- Чем отличается сквозное моделирование от событийного?
- Опишите основной алгоритм событийного логического моделирования.
- Что такое очередь будущих событий?
- Какие вы знаете способы моделирования временного механизма?
- Опишите двухпроходной алгоритм логического моделирования на основе продвижения по очереди будущих событий.
- Какие недостатки имеет этот алгоритм?
- Опишите улучшенный двухпроходной алгоритм логического моделирования.
- Опишите однопроходной алгоритм событийного логического моделирования.



