Формула Бернулли. Формула Пуассона. Наивероятнейшее число наступления событий. Локальная теорема Муавра-лапласса
Пример 3. В ящике лежат 100 отшлифованных поделочных камня и 80 не шлифован-ных. Из ящика извлекают 20 камней. Какое наивероятнейшее число шлифованных камней будет извлечено при этом.
Решение. Определим 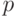 и
и 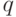 - вероятности извлечения и шлифованного, и не шлифованного поделочного камня. Так как общее число камней в ящике 180, то эти вероятности просто подсчитать:
- вероятности извлечения и шлифованного, и не шлифованного поделочного камня. Так как общее число камней в ящике 180, то эти вероятности просто подсчитать:
![\[ p=\frac {100} {180} = \frac 5 9;\ q=1-\frac 5 9 = \frac 4 9 .\]](/sites/default/files/tex_cache/e0112b4fe7c3d9d765db4bb360651f59.png)
Тогда определим  по формуле (3):
по формуле (3):
![\[ \ 20 \cdot \frac 5 9 -\frac 4 9 \leqslant m_{0} \leqslant 20 \cdot \frac 5 9 + \frac 5 9 .\]](/sites/default/files/tex_cache/a41c920b55ef7db7f760bc5d7cce7371.png)
![\[ 10 \frac 2 3 \leqslant m_{0} \leqslant 11 \frac 2 3.\]](/sites/default/files/tex_cache/7a8f24dd96a672f9d2aff686e44a6c03.png)
Округлим левую границу с избытком, а правую с недостатком получим, что  Т.е. среди 20 извлеченных камней не меньше 11 будут шлифованными.
Т.е. среди 20 извлеченных камней не меньше 11 будут шлифованными.
Часто на практике приходиться решать обратную задачу, когда известно количество , а нужно определить сколько раз необходимо провести испытания.
Пример 4. В ящике лежат 100 шлифованных поделочных камня и 80 не шлифованных. Мастеру необходимо 11 шлифованных камней. Сколько камней, не выбирая, ему надо взять, чтобы среди взятых было нужное количество шлифованных камней?
Решение. Эта задача обратная задаче, рассмотренной в примере 3. Теперь известно  , нужно найти
, нужно найти 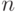 . Для этого выполним простейшее преобразо-вание неравенства (3): отнимем от всех его частей
. Для этого выполним простейшее преобразо-вание неравенства (3): отнимем от всех его частей 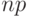 и
и  , получим
, получим
![\[ \ np-q-np-m_{0} \leqslant m_{0}- np – m_{0} \leqslant np + p –np –m_{0}.\]](/sites/default/files/tex_cache/5b832212629196da11f915b00fe13674.png)
![\[ \ -(q+m_{0}) \leqslant –np \leqslant p –m_{0}.\]](/sites/default/files/tex_cache/cc5fd8eda8519e1b83594573c5353346.png)
Умножим последнее неравенство на (- 1) и разделим на 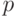 , тогда (при умножении на -1 знаки неравенства меняются на противоположные):
, тогда (при умножении на -1 знаки неравенства меняются на противоположные):
![\[ \ \frac {m_{0}-p} p \leqslant n \leqslant \frac {m_{0}+q} p.\]](/sites/default/files/tex_cache/c6874aab2db1657ba93158963c54bbe1.png) |
( 4) |
Воспользуемся полученной формулой (4) для решения нашего примера.
![\[ \ \frac {11- \frac 5 9} {\frac 5 9} \leqslant n \leqslant \frac {11- \frac 4 9} {\frac 5 9}, \]](/sites/default/files/tex_cache/b864a45213c2dc16349ad6ea90003c2e.png)
откуда
![\[ \ \frac {94} 5 \leqslant n \leqslant \frac {103} 5, \]](/sites/default/files/tex_cache/0c2306f74dce7932a24954bfe503653e.png)
или
![\[ \ 18 \frac 4 5 \leqslant n \leqslant 20 \frac 3 5, \]](/sites/default/files/tex_cache/fe2171e27db367c818b4ad3750917ee9.png)
Округляя до целых, получим, что мастеру надо достать 19 либо 20 камней, чтобы среди них гарантиро-ванно было 11 шлифованных.
Пример 5. Вероятность попадания стрелка в цель равна 0,8. Стрелок делает 20 выстре-лов. определить наивероятнейшее количество попаданий.
Решение. Для решения задачи воспользуемся формулой (3):
![\[ \ 20 \cdot 0,8 - 0,2 \leqslant m_{0} \leqslant 20 \cdot 0,8 +0,8, \]](/sites/default/files/tex_cache/05def83fcfc67d4984a5af6b7458cb70.png)
откуда
![\[ \ 15,8 \leqslant m_{0} \leqslant 16,8. \]](/sites/default/files/tex_cache/3f936a84e60c8c687dcaea888899f8cb.png)
Следовательно, стрелок скорее всего попадет 16 раз.
Если число испытаний большое, 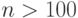 , а вероятность появления события при каждом испытании мала,
, а вероятность появления события при каждом испытании мала, 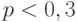 , то для отыскания вероятности что при
, то для отыскания вероятности что при 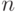 испытаниях некоторое событие случится
испытаниях некоторое событие случится 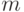 раз используют приближенную формулу Пуассона, которая является обобщением формулы Бернулли:
раз используют приближенную формулу Пуассона, которая является обобщением формулы Бернулли:
![\[ \ P_{m,n} =\frac 1 {\sqrt {npq}} \cdot f(x) \]](/sites/default/files/tex_cache/20719fafca64541816eb733382d9e205.png) |
( 5) |
где
![\[ \ x=\frac {m-np}{\sqrt {npq}}.\]](/sites/default/files/tex_cache/dae842b08d22d76a6d1c319208cee512.png) |
( 6) |
Формулу ( 5) часто называют локальной теоремой Муавра-Лапласса.
Здесь функция 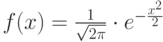 . Существуют специальные таблицы, позволяющие вычислить значение данной функции по ее аргументу. На практике вычисляют
. Существуют специальные таблицы, позволяющие вычислить значение данной функции по ее аргументу. На практике вычисляют 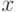 , а затем по таблицам определяют значение функции. Если аргумент получился отрицательным, то значение функции будет такое же, как и при положительном аргументе. Т.е.
, а затем по таблицам определяют значение функции. Если аргумент получился отрицательным, то значение функции будет такое же, как и при положительном аргументе. Т.е. 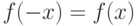 .
.
Если вероятность появления события мала ( 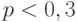 ), то для отыскания того, что испытание состоится
), то для отыскания того, что испытание состоится 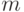 раз, можно воспользоваться формулой Пуассона:
раз, можно воспользоваться формулой Пуассона:
![\[ \ P_{n}(m) \approx \frac {\lambda_{n}^m e^{-\lambda_{n}}} {m!},\]](/sites/default/files/tex_cache/09ab98e38774973a6372967e80058c52.png) |
( 7) |
где  - среднее число появления событий.
- среднее число появления событий.
Если вероятность появления события меняется от испытания к испытанию, но сами испытания независимы, то тогда используется производящая функция  , представляющая собой произведение вероятностных биномов. Эта функция обладает интересным свойством, которое просто проведем здесь без доказательства. После перемножения всех биномов и приведения подобных при
, представляющая собой произведение вероятностных биномов. Эта функция обладает интересным свойством, которое просто проведем здесь без доказательства. После перемножения всех биномов и приведения подобных при 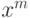 коэффициенты при степенях
коэффициенты при степенях 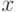 представляют собой вероятность того, что событие появится
представляют собой вероятность того, что событие появится 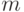 раз в
раз в 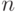 испытаниях, т.е.
испытаниях, т.е.
![\[ \prod\limits_{i \to1}^n \left (q_{i}+p_{i}x \right ) = \sum\limits_{m=0}^n P_{m,n}x^m\]](/sites/default/files/tex_cache/bc7395b4408af4845852c13c38454283.png) |
( 8) |
Пример 6. Связь с шестью дальними партиями была организована через радио посред-ством радиостанций. Каждый отряд в течение дня имеет возможность в любое время связаться с базой, где радиостанция работает круглосуточно. Если вероятность связи с каждым из отрядов 0,8, найти вероятность того, что в данный момент не менее четырех партий вышли на связь.
Решение. Для решения задачи воспользуемся производящей функцией. Определим па-раметры функции: 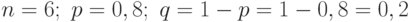 . Построим функцию
. Построим функцию
![\[ \varphi (x) =(0,2-0,8x)^6 =\\= (0,2)^6+6 \cdot (0,2)^5 (0,8x)^1+15 \cdot (0,2)^4 (0,8x)^2 +20 \cdot (0,2)^3 (0,8x)^3 +15 \cdot (0,2)^2 (0,8x)^4+6 \cdot (0,2)^1 (0,8x)^5 +(0,8x)^6 =\\=0,000064+0,001536x+0,01536x^2+0,08192x^3+0,24576x^4+0,393216x^5+0,262144x^6 \]](/sites/default/files/tex_cache/b50ee71025884a2babda1620d2367008.png)
Сумма всех коэффициентов равна 1, в чем можно убедиться самостоятельно. По условию задачи нам не-обходимо учесть коэффициенты при членах 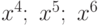 . Тогда искомая вероятность будет равна
. Тогда искомая вероятность будет равна 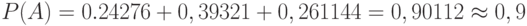
Пример 7. Два специалиста сортируют алмазы, которые затем собирают по размерам. Вероятность ошибки первого 0,1, а второго - 0,3. Из отсортированных алмазов одного размера взяли 2. Най-ти вероятность того, что оба алмаза будут одного размера.
Решение. Для решения задачи воспользуемся производящей функцией. Определим па-раметры функции: для первого специалиста 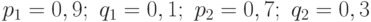 .
.
Построим функцию: 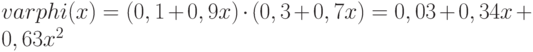 . По условию задачи нам необходимо учесть коэффициент при
. По условию задачи нам необходимо учесть коэффициент при 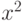 , т.е. искомая вероятность будет равна
, т.е. искомая вероятность будет равна  .
.
Пример 8. Статистикой установлено, что из каждой 1000 родившихся детей в среднем рождается 485 девочек, а остальные - мальчики. В семье 5 детей. Найти вероятность того, что среди этих детей: 3 мальчика.
Решение. Для решения задачи воспользуемся локальной теоремой Муавра – Лапласа, для которой определим необходимые переменные:  .
.
Воспользуемся формулами (5) и (6): 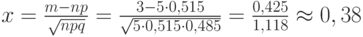 . Из таблицы находим значение функции
. Из таблицы находим значение функции 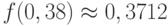
Теперь полученные значения подставим в формулу (5), получим: 
Теорему Бернулли часто используют тогда, когда необходимо оценить вероятность наибольшего отклонения появления событий от ее ожидаемого значения. Случайной величиной в этом случае является число появлений событий и 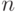 независимых испытаниях. В этом случае теорема Бернулли записывается так:
независимых испытаниях. В этом случае теорема Бернулли записывается так:
![\[ P \left\{ \left | \frac m n –p \right| \leqslant \tau \right\} > 1-\frac {pq} {n\tau^2}\]](/sites/default/files/tex_cache/0a79e29593b8738f16b2a75eef0b4195.png) |
( 9) |
Пример 9. Из 1000 изделий, изготовленных цехом, проверили 200 случайно отобранных изделий. Среди них оказалось 25 изделий с браком. Приняв долю бракованных изделий среди отобранных за вероятность изготовления бракованного изделия, оценить вероятность того, что во всей партии бракованных изделий окажется не более 10%.
Решение. Определим вероятность изготовления бракованного изделия:  . Отклонение частости появлений бракованных изделий от вероятности
. Отклонение частости появлений бракованных изделий от вероятности 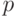 по абсолютной величине равно
по абсолютной величине равно 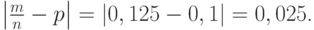 Число испытаний 1000. Используем формулу (9) и находим искомую вероятность:
Число испытаний 1000. Используем формулу (9) и находим искомую вероятность:
![\[ P \left\{ \left | \frac m n –p \right| \leqslant 0,025 \right\} > 1-\frac {0,125 \cdot 0,875} {1000 \cdot 0,025^2},\]](/sites/default/files/tex_cache/f1e8732ae22ec956f02e192b13bec041.png)
откуда 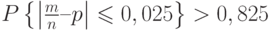 - получаем ответ.
- получаем ответ.
