|
В уравнениях движения кривошипно-шатунного механизма вместо обозначения радиуса кривошипа "r" ошибочно записан символ "?" (гамма). P.S. Может быть это слишком очевидно, но не упомянуто, что угол поворота кривошипа ? считается малым. |
Компьютерное моделирование и решение нелинейных уравнений
Численные методы решения дифференциальных уравнений первого порядка
Общий вид дифференциального уравнения
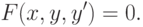 |
( 12.1) |
Нормальная форма дифференциального уравнения
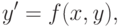 |
( 12.2) |
где
y=y(x) -неизвестная функция, подлежащая определению,
f(x,y) - правая часть дифференциального уравнения в нормальной форме, равная первой производной функции y(x). В функцию f(x,y) помимо аргумента x входит и сама неизвестная функция y(x).
Пример:
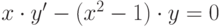 - общий вид дифференциального уравнения первого порядка,
- общий вид дифференциального уравнения первого порядка,
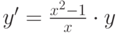 - нормальная форма этого же уравнения.
- нормальная форма этого же уравнения.
Если неизвестная функция у зависит от одного аргумента x, то дифференциальное уравнение вида
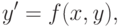
Если функция у зависит от нескольких аргументов, то такое дифференциальное уравнение называется дифференциальным уравнением в частных производных.
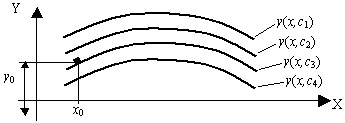
Общим решением обыкновенного дифференциального уравнения
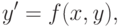
При решении прикладных задач ищут частные решения дифференциальных уравнений. Выделение частного решения из семейства общих решений осуществляется с помощью задания начальных условий:
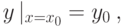 |
( 12.3) |
Нахождение частного решения дифференциального уравнения
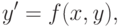 |
( 12.4) |
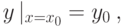 |
( 12.3) |
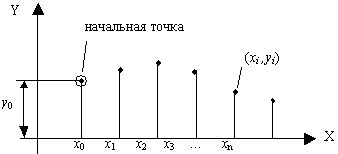
В численных методах задача Коши ставится следующим образом:
найти табличную функцию 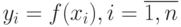 которая удовлетворяет заданному дифференциальному уравнению (12.2) и начальному условию (12.3) на отрезке [a,b] с шагом h, то есть найти таблицу
которая удовлетворяет заданному дифференциальному уравнению (12.2) и начальному условию (12.3) на отрезке [a,b] с шагом h, то есть найти таблицу
Здесь
h - шаг интегрирования дифференциального уравнения,
a=x0 - начало участка интегрирования уравнения,
b=xn - конец участка,
n=(b-a)/h - число шагов интегрирования уравнения.
На графике (рис 12.9) решение задачи Коши численными методами представляется в виде совокупности узловых точек с координатами (xi ,yi), 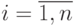 .
.