|
В уравнениях движения кривошипно-шатунного механизма вместо обозначения радиуса кривошипа "r" ошибочно записан символ "?" (гамма). P.S. Может быть это слишком очевидно, но не упомянуто, что угол поворота кривошипа ? считается малым. |
Компьютерное моделирование и решение нелинейных уравнений
Решение дифференциальных уравнений высоких порядков
Методы Рунге-Кутта можно использовать не только для решения дифференциальных уравнений первого порядка
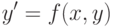
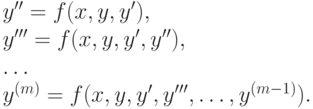
Любое дифференциальное уравнение m-го порядка
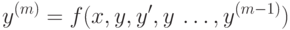 |
( 12.8) |
можно свести к системе, состоящей из m уравнений первого порядка при помощи замен.
Заменим:
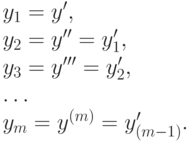
В результате дифференциальное уравнение m -го порядка (12.8) сводится к системе, состоящей из m дифференциальных уравнений первого порядка:
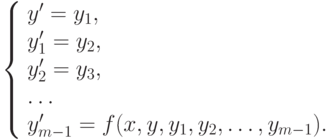 |
( 12.9) |
Решением системы (12.2), а значит и дифференциального уравнения m -го порядка (12.1) является m табличных функций 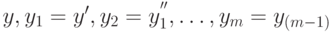
Решение дифференциальных уравнений второго порядка
В задачах моделирования динамических систем наиболее часто приходится решать дифференциальные уравнения второго порядка.
Общий вид дифференциальных уравнений второго порядка:
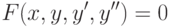 |
( 12.10) |
Нормальная форма дифференциальных уравнений второго порядка:
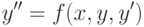 |
( 12.11) |
Пример
Уравнение в общем виде
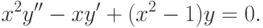
Его нормальная форма
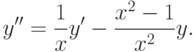 |
( 12.12) |
Дифференциальное уравнение второго порядка (12.11) можно свести к системе, состоящей из двух дифференциальных уравнений первого порядка при помощи замен.
Заменим y1=y',
Тогда y'1=y".
В результате уравнение (12.11) сводится к системе, состоящей из двух дифференциальных уравнений первого порядка:
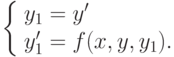
Для примера (12.12) эта система имеет вид:
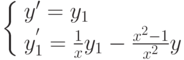 |
( 12.13) |
Решением этой системы являются две функции y(x) и y1(x),
где
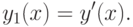
Сформулируем задачу Коши для системы, состоящей из двух дифференциальных уравнений второго порядка.
Дана система
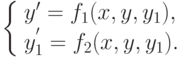 |
( 12.14) |
Даны два начальных условия:
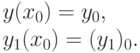
Необходимо проинтегрировать систему на участке [a, b] с шагом h.
В численных методах задача Коши для системы (12.14) ставится следующим образом:
Найти табличные функции
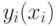 и
и 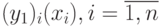 ,
т.е. найти таблицу
,
т.е. найти таблицу
Здесь
h - шаг интегрирования дифференциального уравнения,
a=x0 - начало участка интегрирования уравнения,
b=xn - конец участка,
n=(b-a)/h - число шагов интегрирования уравнения.
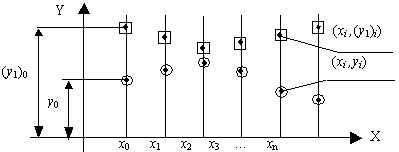
На графике решением задачи Коши для системы, состоящей из двух дифференциальных уравнений первого порядка, является совокупность узловых точек (рис. 12.15).
При этом на каждом шаге, т.е. для каждого значения xi решением являются две узловые точки с координатами (xi, yi), (xi, (y1)i).
Для решения системы дифференциальных уравнений используем те же методы, что и для решения одного дифференциального уравнения первого порядка. При этом необходимо соблюдать условие: на каждом шаге интегрирования, т. е. в точках с координатами х1 , х2 , х3 , : , хn все уравнения системы надо решать параллельно.