Скрытые параметры и транспонированная регрессия
Интерполяция свойств химических элементов
Идея интерполяции свойств элементов возникла в химии еще до создания периодической системы [7.7]. В триадах Деберейнера (1817г.) характеристики среднего элемента триады находились как средние арифметические значений характеристик крайних элементов. Были попытки работать с тетрадами, "эннеадами" (составленными из трех триад) и т.п. Периодическая таблица Менделеева позволяет по-разному определять группу ближайших соседей для интерполяции: от двух вертикальных соседей по ряду таблицы до окружения из восьми элементов (два из того же ряда и по три из соседних рядов). Однако интерполяция свойств путем взятия среднего арифметического по ближайшим элементам таблицы не всегда (не для всех свойств и элементов) дает приемлемые результаты - требуется либо иной выбор соседей, либо другая процедура интерполяции.
Более общим образом задачу интерполяции можно поставить так: найти для каждого элемента наилучшую формулу, выражающую его вектор свойств через векторы свойств других элементов. Эту задачу и решает метод транспонированной регрессии.
В работах [7.9, 7.10] исследовался полуэмпирический метод, близкий по идее к методу транспонированной регрессии. Единственное и главное отличие заключалось в том, что среди параметров сразу фиксировался набор "теоретических" и строились зависимости остальных свойств от них (в частности, зависимости потенциалов ионизации от атомного номера).
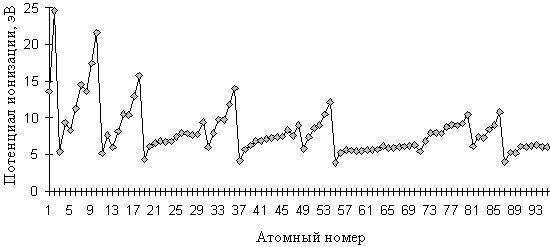
Используем метод транспонированной линейной регрессии для интерполяции и прогноза высших потенциалов ионизации (ПИ). Напомним, что n -й потенциал ионизации A - энергия, которую необходимо затратить, чтобы оторвать n -й электрон от иона A(n-1)+ ( n-1 раз ионизированного атома A ). Зависимость ПИ от атомного номера ( рис. 7.1) нелинейна и сложна.
Следуя формальному смыслу, n -й ПИ атома A следует относить все к тому же атому. Однако структура энергетических уровней иона определяется зарядом ядра и числом электронов. Для атома оба этих числа совпадают с атомным номером, но для ионов уже различны. Как и в работах [7.9, 7.10], n -й потенциал ионизации атома с атомным номером m будем искать как функцию от m-n+1. Объектами будут служить, строго говоря, не атомы с атомным номером m, а m -электронные системы. Таким образом, второй ПИ гелия (атомный номер 2), третий ПИ лития (атомный номер 3) и т.д. относятся к одноэлектронной системе при различных зарядах ядра. Осуществляется привязка потенциала ионизации уже ионизированного атома не к этому же атому, а к m -электронной системе с m, равным имеющемуся числу электронов в ионе.
Рассмотрим результаты пробного прогноза высших потенциалов ионизации. Приведем результаты, полученные при использовании в функции критерия нормы в виде суммы абсолютных значений компонент вектора и значения 
, поскольку такое сочетание при тестировании показало себя наилучшим образом. Для того, чтобы невязки по каждому свойству равномерно входили в левую часть функции критерия, выполнялось нормирование каждого свойства (приведение к нулевому математическому ожиданию и единичному среднеквадратическому уклонению).
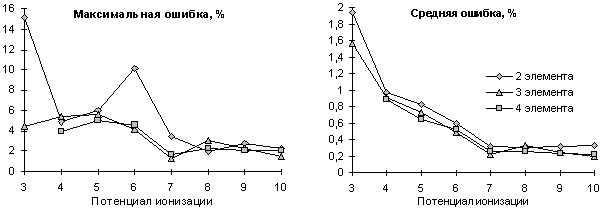
Рис. 7.2. Зависимость ошибки прогноза 3-10 ПИ от числа элементов в опорной группе. Опорные группы и регрессионные зависимости для каждого ПИ строились по предыдущим ПИ
На рис. 7.2 показаны ошибки прогноза ПИ (с 3-го по 10-й) при разных размерах опорных групп (2, 3 и 4 элемента в опорной группе). При этом для каждого ПИ опорные группы строились по предыдущим ПИ. Величины максимальной и средней ошибок показаны в процентах от диапазона изменения величин соответствующего ПИ. На основе приведенных графиков можно рекомендовать использование как можно большего набора однородных свойств для достижения оптимального прогноза.
Для попытки прогноза отсутствующих в справочной литературе [7.11, 7.12] значений высших ПИ (с 5-го по 10-й ПИ для элементов с атомными номерами от 59-го до 77-го) изучим влияние размера опорной группы на точность прогноза при построении опорной группы по первым четырем ПИ ( Рис. 7.3). Удовлетворительная точность достигается при трех и четырех элементах в опорной группе.
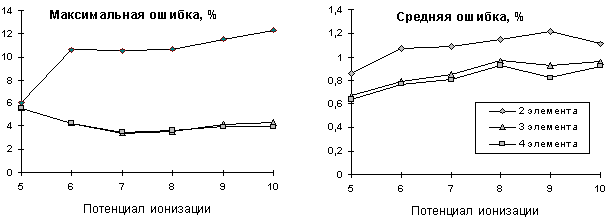
Рис. 7.3. Зависимость ошибок прогноза 5-10 ПИ от числа элементов в опорной группе. Опорные группы и регрессионные зависимости строились по первым четырем ПИ
Дальнейшее увеличение числа элементов в опорной группе себя не оправдывает. Увеличению точности прогноза мешают и погрешности при экспериментальном определении ПИ, особенно высших. В таблице 7.2 таблица 7.2 приводится прогноз отсутствующих значений ПИ.