Скрытые параметры и транспонированная регрессия
Теорема о скрытых параметрах
Ряд алгоритмов решения проблемы скрытых параметров можно построить на основе следующей теоремы. Пусть n - число свойств, N - количество объектов, 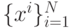 - множество векторов значений признаков. Скажем, что в данной группе объектов выполняется уравнения регрессии ранга r, если все векторы
- множество векторов значений признаков. Скажем, что в данной группе объектов выполняется уравнения регрессии ранга r, если все векторы 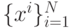 принадлежат n-r -мерному линейному многообразию. Как правило, в реальных задачах выполняется условие N>n. Если же
принадлежат n-r -мерному линейному многообразию. Как правило, в реальных задачах выполняется условие N>n. Если же 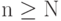 , то векторы
, то векторы 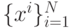 принадлежат N-1 -мерному линейному многообразию и нетривиальные регрессионные связи возникают лишь при ранге r>n-N+1. Ранг регрессии r измеряет, сколько независимых линейных связей допускают исследуемые свойства объектов. Число r
является коразмерностью того линейного подпространства в пространстве векторов признаков, которому принадлежат наблюдаемы векторы признаков объектов. Разумеется, при обработке реальных экспериментальных данных необходимо всюду добавлять "с заданной точностью", однако пока будем вести речь о точных связях.
принадлежат N-1 -мерному линейному многообразию и нетривиальные регрессионные связи возникают лишь при ранге r>n-N+1. Ранг регрессии r измеряет, сколько независимых линейных связей допускают исследуемые свойства объектов. Число r
является коразмерностью того линейного подпространства в пространстве векторов признаков, которому принадлежат наблюдаемы векторы признаков объектов. Разумеется, при обработке реальных экспериментальных данных необходимо всюду добавлять "с заданной точностью", однако пока будем вести речь о точных связях.
Следующая теорема о скрытых параметрах позволяет превращать вопрос о связях между различными свойствами одного объекта (одной и той же для разных объектов) в вопрос о связи между одним и тем же свойством различных объектов (одинаковой связи для различных свойств) - транспонировать задачу регрессии. При этом вопрос о качественной неоднородности выборки "транспонируется" в задачу поиска для каждого объекта такой группы объектов (опорной группы), через свойства которых различные свойства данного объекта выражаются одинаково и наилучшим образом.
Теорема. Пусть для некоторого r>0 существует такое разбиение 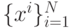 на группы
на группы
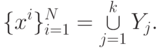
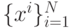 найдется такое множество Wi (опорная группа объекта xi ) из k объектов, что
найдется такое множество Wi (опорная группа объекта xi ) из k объектов, что  и для некоторого набора коэффициентов
и для некоторого набора коэффициентов 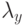
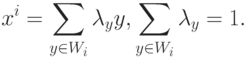 |
( 1) |
Последнее означает, что значение каждого признака объекта xi является линейной функцией от значений этого признака для объектов опорной группы. Эта линейная функция одна и та же для всех признаков.
Линейная зависимость (1) отличается тем, что она инвариантна к изменениям единиц измерения свойств и сдвигам начала отсчета. Действительно, пусть координаты всех векторов признаков подвергнуты неоднородным линейным преобразованиям: 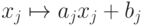 , где j - номер координаты. Нетрудно убедиться, что при этом линейная связь (1) сохранится. Инвариантность относительно преобразования масштаба обеспечивается линейностью и однородностью связи, а инвариантность относительно сдвига начала отсчета - еще и тем, что сумма коэффициентов
, где j - номер координаты. Нетрудно убедиться, что при этом линейная связь (1) сохранится. Инвариантность относительно преобразования масштаба обеспечивается линейностью и однородностью связи, а инвариантность относительно сдвига начала отсчета - еще и тем, что сумма коэффициентов 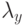 равна 1.
равна 1.
Сформулированная теорема позволяет переходить от обычной задачи регрессии (поиска зависимостей значения признака от значений других признаков того же объекта) к транспонированной задаче регрессии - поиску линейной зависимости признаков объекта от признаков других объектов и отысканию опорных групп, для которых эта зависимость является наилучшей.
Доказательство основано на том, что на каждом k -мерном линейном многообразии для любого набора из q точек y1, y2, ..., yq при q>k+1 выполнено соотношение
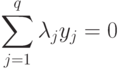
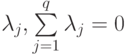 и некоторые
и некоторые  .
.С математической точки зрения теорема о скрытых параметрах представляет собой вариант утверждения о равенстве ранга матрицы, вычисляемого по строкам, рангу, вычисляемому по столбцам.
