Скрытые параметры и транспонированная регрессия
Система уравнений решается для известных значений компонент вектора y, полученное решение используется для предсказания неизвестных значений.
В случае критерия б) в качестве начального приближения для каждого испытуемого набора рассматривались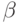 
минимизирующие невязку 
. Минимум критерия находился BFGS -методом [7.8].
Нами рассмотрен вариант нахождения оптимальной опорной группы фиксированного размера в задаче транспонированной линейной регрессии, когда оптимальная опорная группа отбиралась в ходе полного перебора всех возможных опорных групп. Другой предложенный вариант (оптимизационный) предполагает первоначальное задание избыточного числа объектов в опорной группе и последующее сокращение ее размера в результате отбрасывания наименее значимых параметров.
Программная реализация и переборного, и оптимизационного вариантов решения транспонированной задачи линейной регрессии выполнялась в среде MS DOS с использованием транслятора Borland C++. Текст программы соответствует ANSI -стандарту языка C++, что делает возможным перенос программы на другие аппаратные платформы (что и делалось большие базы медицинских данных обрабатывалась на компьютере Alpha Station корпорации DEC ). При этом зависимые от операционной системы фрагменты программы подключаются при помощи условных директив препроцессора языка. Так, для обеспечения работы с большими файлами данных в среде MS DOS используется обращение к интерфейсу DPMI (предоставляется DPMI -расширителями и операционными системами OS/2, Windows 3.xx, Windows 95, Windows NT ) для переключения в защищенный режим и обхода ограничения в 640К памяти.
Программа позволяет пользователю определять файл данных, обрабатываемые строки (объекты) и столбцы (свойства объектов), выбирать между вариантами решения и видами функции критерия, задавать значения иных параметров метода. Для обработки порядковых признаков возможна спецификация некоторых столбцов, как содержащих значения не из непрерывного, а из дискретного множества значений. Прогнозные значения отсутствующих данных в этом случае будут приводиться к ближайшему значению из дискретного множества значений.
Результатом работы программы является файл отчета. Для каждого обрабатываемого объекта (строки базы данных) в файле отчета содержится информация об оптимальным образом приближающей объект опорной группе (номера объектов, входящих в опорную группу, и коэффициенты разложения), значение функции критерия, ошибки интерполяции известных свойств объекта и прогнозные значения для неизвестных свойств. В конце файла отчета выводятся максимальные и средние ошибки аппроксимации известных данных для всех обрабатываемых столбцов базы данных (свойств объектов).
Тестирование предлагаемого метода проводилось на модельных данных. При построении модельных данных задаются размерность теоретической проекции (число скрытых переменных), размерность эмпирической проекции (число свойств объекта), число различных классов, вектор среднего и разброса для генерируемых данных в каждом классе. Для каждого класса случайным образом порождается линейный оператор, отображающий пространство скрытых переменных в пространство свойств объектов. Для каждого объекта случайным образом выбираются значения скрытых переменных и рассчитываются значения свойств. Тестирование проводилось в скользящем режиме по всему задачнику. Полученные результаты (Табл.1 таблица 7.1) позволяют заключить, что предложенный метод весьма эффективен, критерий вида б) с большей эффективностью определяет опорную группу при избыточном и недостаточном наборах объектов (лучше, чем МНК а) ), а решение вида (2) дает лучшие по сравнению с (3) результаты при избыточном наборе объектов.
 |
критерий | вид | средняя относительная ошибка, % | |||
|---|---|---|---|---|---|---|
| при размере опорной группы | ||||||
| 3 | 4 | 5 | 18 | |||
| 0.01 | а | 1 | 5 | 0 | 15 | 66 |
| а | 2 | 5 | 0 | 15 | 66 | |
| б | 1 | 5 | 0 | 13 | 40 | |
| б | 2 | 5 | 0 | 13 | 66 | |
| 0.1 | а | 1 | 10 | 16 | 30 | 72 |
| а | 2 | 10 | 16 | 30 | 72 | |
| б | 1 | 6 | 10 | 14 | 40 | |
| б | 2 | 6 | 10 | 14 | 66 | |
При решении задачи заполнения пробелов в таблицах данных для любой таблицы общей рекомендацией является проведение серии пробных прогнозов для определения оптимального сочетания параметров.