Эволюционное программирование
10.5. Современные направления эволюционного программирования
В настоящее время известны многочисленные модификации ЭП, которые сильно отличаются от классического ЭП и фактически пересекаются с другими эволюционными алгоритмами, в первую очередь, эволюционными стратегиями (ЭС). В середине восьмидесятых годов в ЭП в качестве генома стали использоваться не только конечные автоматы, но и произвольные структуры данных [3]. Это позволяет с успехом применять ЭП при численной оптимизации и решении задач комбинаторной оптимизации.
В современных работах в качестве особи в ЭП все чаще используется вектор вещественных чисел  . Рассмотрим этот подход на примере минимизации непрерывной неограниченной функции
. Рассмотрим этот подход на примере минимизации непрерывной неограниченной функции 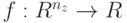 . Обозначим через
. Обозначим через 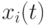 потенциальное
потенциальное  -е решение в поколении
-е решение в поколении  , у которого каждая компонента
, у которого каждая компонента 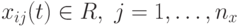 . Потомок генерируется из родителя с помощью оператора мутации следующим образом:
. Потомок генерируется из родителя с помощью оператора мутации следующим образом:
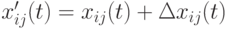
где 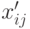 – компонента вектора потомка и
– компонента вектора потомка и 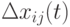 - шаг мутации. Размер шага определяется стохастически в соответствии с некоторым вероятностным распределением, где девиация (отклонение) шума задается параметром
- шаг мутации. Размер шага определяется стохастически в соответствии с некоторым вероятностным распределением, где девиация (отклонение) шума задается параметром 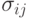 . В общем виде размер шага вычисляется в соответствии с выражением
. В общем виде размер шага вычисляется в соответствии с выражением 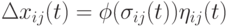 , где
, где 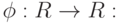 - функция, которая масштабирует вклад шума
- функция, которая масштабирует вклад шума 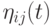 .
.
На базе характеристик масштабирующей функции  можно разбить алгоритмы ЭП на три группы:
можно разбить алгоритмы ЭП на три группы:
- Неадаптивное ЭП, в котором
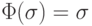 , где отклонения размера шага остаются постоянными.
, где отклонения размера шага остаются постоянными. - Динамическое ЭП, где отклонение размера шага изменяется с течением времени в соответствии с некоторой детерминированной функцией (как правило, фитнесс-функцией особи).
- Самоадаптивное ЭП, в котором отклонение размера шага изменяется динамически. При этом лучшие значения
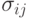 отслеживаются параллельно с значениями переменных
отслеживаются параллельно с значениями переменных 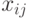 .
.
Поскольку девиация 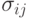 в значительной степени определяет поведение особи в случае динамического или самоадаптивного ЭП, они относятся к важнейшим параметрам ЭП. При этом каждая особь имеет свою стратегию параметров, в которой каждая особь представляется кортежем
в значительной степени определяет поведение особи в случае динамического или самоадаптивного ЭП, они относятся к важнейшим параметрам ЭП. При этом каждая особь имеет свою стратегию параметров, в которой каждая особь представляется кортежем 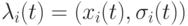 . Кроме девиации, которая является наиболее популярным параметром в ЭП, в некоторых работах [6,7] ЭП используются коэффициенты корреляции между компонентами особи, что фактически заимствовано из ЭС.
. Кроме девиации, которая является наиболее популярным параметром в ЭП, в некоторых работах [6,7] ЭП используются коэффициенты корреляции между компонентами особи, что фактически заимствовано из ЭС.
Как и любой эволюционный алгоритм, ЭП основано на стохастическом поиске. Здесь стохастичность вводится в вычисление размера шага, как функции шума 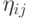 , соответствующей некоторому вероятностному распределению. Следующие основные вероятностные распределения используются для указанных целей:
, соответствующей некоторому вероятностному распределению. Следующие основные вероятностные распределения используются для указанных целей:
Однородное. Здесь шум формируется согласно однородному распределению 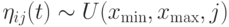 , где
, где 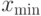 и
и  определяют нижнюю и верхнюю границы изменения диапазона значений
определяют нижнюю и верхнюю границы изменения диапазона значений 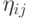 . Отметим, что
. Отметим, что ![E[\eta_{ij}]=0](/sites/default/files/tex_cache/c711beeeca614cdaf85df8d72d6159c9.png) предотвращает любое смещение индуцированного шума, где
предотвращает любое смещение индуцированного шума, где ![E[\cdot]](/sites/default/files/tex_cache/0a6e744af36c68c135ff687e7028bedc.png) означает оператор математического ожидания.
означает оператор математического ожидания.
В [8] предложен оператор однородной мутации, который выполняется в соответствии с выражением 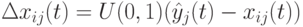 , где
, где 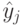 представляет лучшую особь текущей популяции
представляет лучшую особь текущей популяции 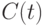 . Этот оператор мутации заставляет все особи сделать случайное движение в сторону лучшей особи (подобно социальной компоненте в роевых алгоритмах). При этом лучшая особь не изменяется.
. Этот оператор мутации заставляет все особи сделать случайное движение в сторону лучшей особи (подобно социальной компоненте в роевых алгоритмах). При этом лучшая особь не изменяется.
Гауссово. Для Гауссова оператора мутации шум формируется в соответствии с нормальным распределением с нулевым средним значением ![[6,9]:\eta_{ij}(t)\sim N(0,\sigma_{ij}(t))](/sites/default/files/tex_cache/330d9d9e8da55ce5ebc1454d68302c8c.png) , где плотность функции Гаусса задается как
, где плотность функции Гаусса задается как 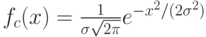 с отклонением
с отклонением  .
.
Коши. При выполнении оператора мутации Коши 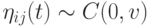 , где
, где  - масштабируюший коэффициент и функция плотности центрирована и определяется следующим образом:
- масштабируюший коэффициент и функция плотности центрирована и определяется следующим образом:

Тогда соответствующая функция распределения определяется как 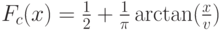 . Отметим, что распределение Коши имеет более широкий "хвост" и поэтому данный оператор дает большие значения, чем Гауссов.
. Отметим, что распределение Коши имеет более широкий "хвост" и поэтому данный оператор дает большие значения, чем Гауссов.
Леви. В этом распределении 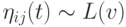 , где центрированная функция вероятностей Леви определяется как
, где центрированная функция вероятностей Леви определяется как 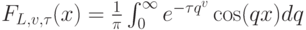 ,где
,где  - масштабирующий множитель и значения
- масштабирующий множитель и значения  контролируют форму распределения. Отметим, что в случае
контролируют форму распределения. Отметим, что в случае 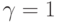 получается распределение Коши, а при
получается распределение Коши, а при 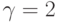 - распределение Гаусса. При
- распределение Гаусса. При  плотность распределения Леви можно аппроксимировать как
плотность распределения Леви можно аппроксимировать как  . Алгоритм генерации случайных чисел Леви дан в работе [10].
. Алгоритм генерации случайных чисел Леви дан в работе [10].
Экспоненциальное. В этом случае  и функция плотности двойного экспоненциального вероятностного распределения определяется так:
и функция плотности двойного экспоненциального вероятностного распределения определяется так:
 , где параметр
, где параметр  управляет вариацией (которая равна
управляет вариацией (которая равна  ). При этом случайные числа генерируются в соответствии со следующими правилами:
). При этом случайные числа генерируются в соответствии со следующими правилами: 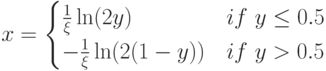 , где
, где  . Следует отметить, что
. Следует отметить, что  .
.
Хаос. Распределение хаоса также может быть использовано для шумовой составляющей  , где
, где 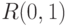 представляет хаотическую последовательность в диапазоне (-1,1). Эту последовательность можно генерировать в соответствии с выражением
представляет хаотическую последовательность в диапазоне (-1,1). Эту последовательность можно генерировать в соответствии с выражением 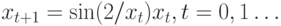 .
.
Комбинированные (сложные) распределения. В некоторых работах предложено использовать комбинированные распределения, например в[11] введен оператор средней мутации (mean mutation operator - MMO), где применяется линейная комбинация распределений Гаусса и Коши. В этом случае 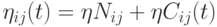 , где
, где 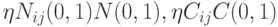 . Результирующее распределение порождает большие мутации, чем Гауссово распределение, но меньшие, чем распределение Коши.
. Результирующее распределение порождает большие мутации, чем Гауссово распределение, но меньшие, чем распределение Коши.
Таким образом, в настоящее время имеется богатый выбор различных видов операторов мутации. Вопрос в том, как различные распределения влияют в процессе поиска решения на расширение или эксплуатацию в пространстве решений. Для достижения хороших характеристик необходимо соблюдать баланс между малыми и большими величинами мутации. Распределение Коши вследствие более широкого "хвоста" порождает большие значения мутации, чем распределение Гаусса. Поэтому распределение Коши больше, чем распределение Гаусса способствует расширению пространства поиска. Поэтому распределение Коши хорошо использовать на начальном этапе поиска решения. Но с другой стороны, мутации на базе распределения Коши работают хуже, чем распределение Гаусса при тонкой коррекции решений на заключительном этапе поиска решений. Распределение Леви дает значения между величинами, порождаемыми распределениями Гаусса и Коши. Поэтому это распределение имеет лучший баланс в расширении и эксплуатации в процессе поиска решения и поэтому предпочтительней.
Другим важнейшим фактором, влияющим на баланс расширения эксплуатации пространства поиска, является метод определения значений параметров ЭП, поскольку размер шага мутации непосредственно зависит от этих параметров.
Выбор вида оператора генетического отбора также играет важную роль для сходимости алгоритма поиска. В классическом ЭП следующая популяция формируется как из особей-родителей, так и особей-потомков. То есть родители и потомки конкурируют в борьбе за выживание. В отличие от других эволюционных алгоритмов, конкуренция основана на использовании относительных, а не абсолютных значений фитнесс-функции. Абсолютное значение фитнесс-функции характеризует насколько данное решение близко к оптимальному. С другой стороны, относительное значение фитнесс-функции показывает насколько оно хорошо по сравнению с группой случайным образом выбранных особей (отобранных из родителей и потомков).
Обозначим через  число родительских особей и через
число родительских особей и через  - число потомков. На первом этапе отбора для каждого родителя
- число потомков. На первом этапе отбора для каждого родителя 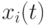 или потомка
или потомка 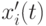 необходимо вычислить значение относительной фитнесс-функции. Определим пул конкуренции
необходимо вычислить значение относительной фитнесс-функции. Определим пул конкуренции  и особь
и особь 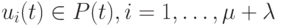 , принадлежащую этому пулу. Для каждой особи пула
, принадлежащую этому пулу. Для каждой особи пула  случайным образом генерируется
случайным образом генерируется 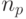 конкурентов из оставшихся особей пула
конкурентов из оставшихся особей пула 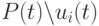 . Тогда значение фитнесс-функции для каждой особи
. Тогда значение фитнесс-функции для каждой особи 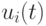 вычисляется следующим образом:
вычисляется следующим образом:
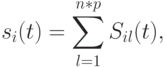
где (в случае минимизации) 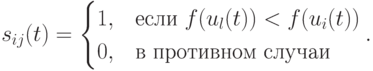 .
.
В работе [12] предложен более "мягкий" подход, где число успешных исходов вычисляется согласно следующей формуле 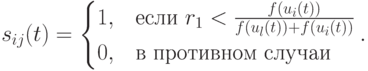 , где
, где 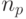 оппонентов выбирается согласно выражению
оппонентов выбирается согласно выражению 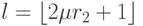 и
и 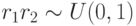 . При этом в случае значительного превосходства
. При этом в случае значительного превосходства 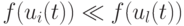 с высокой вероятностью значение фитнесс-функции увеличивается на 1.
с высокой вероятностью значение фитнесс-функции увеличивается на 1.
Основываясь на полученных значениях фитнесс-функции для каждой особи, далее выполняется отбор особей одним из методов, рассмотренных в разделе 3 (элитизма, турнира, рулетки, ранжирования и т.п.).
Кроме этого, различные методы можно использовать для отбора особи (родителя или потомка) в популяцию следующего поколения. Часто используется следующий подход, где выбирается по абсолютным значениям фитнесс-функции лучший потомок данного родителя и принимается решение о том, кто из них перейдет в следующее поколение согласно методу моделирования отжига. То есть потомок 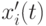 выживает в следующем поколении если:
выживает в следующем поколении если:
-
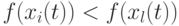 , или
, или -
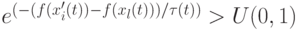 ,
,
где  - температурный коэффициент с
- температурный коэффициент с 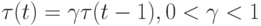 , иначе в следующем поколении выживает родительская особь. В этом случае, согласно методу моделирования отжига имеет шанс выжить особь с худшим значением фитнесс-функции.
, иначе в следующем поколении выживает родительская особь. В этом случае, согласно методу моделирования отжига имеет шанс выжить особь с худшим значением фитнесс-функции.
