Диаграммы
Теорема 71. Пусть даны две теории (с равенством)  и
и  некоторой сигнатуры. Тогда следующие свойства равносильны:
некоторой сигнатуры. Тогда следующие свойства равносильны:
(а) существует нормальная модель теории  и ее расширение,
являющееся нормальной моделью теории
и ее расширение,
являющееся нормальной моделью теории  ;
;
(б) объединение  со всеми
со всеми  -теоремами теории
-теоремами теории  совместно;
совместно;
(в) объединение  со всеми
со всеми 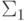 -теоремами теории
-теоремами теории  совместно.
совместно.
Прежде всего отметим, что из (а) очевидно следуют (б) и (в). В
самом деле, если 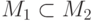 — модели соответствующих
теорий, то в
— модели соответствующих
теорий, то в 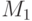 истинны все теоремы теории
истинны все теоремы теории  и все
и все  -теоремы теории
-теоремы теории  (поскольку они наследуются
из
(поскольку они наследуются
из  ), а в
), а в  истинны все теоремы
теории
истинны все теоремы
теории  и все
и все 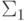 -теоремы теории
-теоремы теории  .
.
Легко проверить, что симметричные условия (б) и (в) равносильны
друг другу, а также такому свойству: не существует 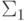 -
теоремы
-
теоремы  теории
теории  и отрицающей ее
и отрицающей ее  -теоремы
-теоремы 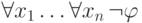 теории
теории  . Пусть, например, теория
. Пусть, например, теория  несовместна с
несовместна с  -следствиями теории
-следствиями теории  . В этом
противоречии участвует конечное число
. В этом
противоречии участвует конечное число  -формул,
которые можно объединить в одну. Получится
-формул,
которые можно объединить в одну. Получится  -формула, она
будет выводима в теории
-формула, она
будет выводима в теории  , а ее отрицание — в
, а ее отрицание — в  .
.
Нам осталось доказать, что любое из свойств (б) и (в) влечет (а).
Здесь нам придется нарушить симметрию и использовать именно (б).
По условию есть интерпретация 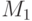 , в которой истинны все
теоремы теории
, в которой истинны все
теоремы теории  и все
и все  -теоремы
теории
-теоремы
теории  . Согласно теореме 70 найдется ее
расширение
. Согласно теореме 70 найдется ее
расширение  , являющееся моделью
, являющееся моделью  , что и
требовалось доказать.
, что и
требовалось доказать.
Можно было бы пытаться рассуждать симметричным образом,
начав с модели теории  , в которой истинны все
, в которой истинны все  -теоремы теории
-теоремы теории  , и пытаться выделить в ней подструктуру, являющуюся
моделью теории
, и пытаться выделить в ней подструктуру, являющуюся
моделью теории  . Однако этот план не проходит, поскольку
аналог теоремы 70 для подструктур неверен.
. Однако этот план не проходит, поскольку
аналог теоремы 70 для подструктур неверен.
149. Покажите, что возможна такая ситуация: все 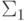 -теоремы
некоторой теории
-теоремы
некоторой теории  истинны в некоторой
интерпретации
истинны в некоторой
интерпретации  , но
, но  не имеет подструктуры, являющейся моделью теории
не имеет подструктуры, являющейся моделью теории  .
(Указание. Рассмотрим теорию линейно упорядоченных множеств без
минимального элемента. Все ее
.
(Указание. Рассмотрим теорию линейно упорядоченных множеств без
минимального элемента. Все ее 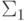 -следствия верны в
-следствия верны в  , поскольку переносятся
из
, поскольку переносятся
из 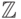 , поэтому в силу элементарной эквивалентности
верны и в
, поэтому в силу элементарной эквивалентности
верны и в 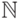 .)
.)
Вот еще одно следствие доказанных в этом разделе результатов.
Теорию  называют
называют  -аксиоматизируемой,
если существует множество
-аксиоматизируемой,
если существует множество  -формул, из которого
выводятся все теоремы теории
-формул, из которого
выводятся все теоремы теории  и только они.
и только они.
Напомним, что нормальная интерпретация  сигнатуры
сигнатуры  является подструктурой нормальной интерпретации
является подструктурой нормальной интерпретации  той
же сигнатуры, если
той
же сигнатуры, если  является расширением
является расширением  , то есть
носитель интерпретации
, то есть
носитель интерпретации  есть подмножество носителя
интерпретации
есть подмножество носителя
интерпретации  и функциональные и предикатные символы
интерпретируются одинаково на аргументах из
и функциональные и предикатные символы
интерпретируются одинаково на аргументах из  .
(Другими словами, чтобы задать какую-либо подструктуру данной
нормальной интерпретации
.
(Другими словами, чтобы задать какую-либо подструктуру данной
нормальной интерпретации  , нужно выбрать подмножество
носителя
, нужно выбрать подмножество
носителя  , замкнутое относительно сигнатурных операций.)
, замкнутое относительно сигнатурных операций.)
Теорема 72 (Лося-Тарского). Теория  -аксиоматизируема
тогда и только тогда, когда она устойчива относительна перехода к подструктурам, то есть
когда любая подструктура любой ее нормальной модели является ее
моделью.
-аксиоматизируема
тогда и только тогда, когда она устойчива относительна перехода к подструктурам, то есть
когда любая подструктура любой ее нормальной модели является ее
моделью.
Очевидно,  -аксиоматизируемая теория устойчива
относительно перехода к подструктурам (все формулы из ее
-аксиоматизируемая теория устойчива
относительно перехода к подструктурам (все формулы из ее  -аксиоматизации остаются истинными). Обратно, пусть
-аксиоматизации остаются истинными). Обратно, пусть  — произвольная теория, устойчивая относительно перехода к
подструктурам. Рассмотрим множество
— произвольная теория, устойчивая относительно перехода к
подструктурам. Рассмотрим множество  всех
всех  -
формул, выводимых в
-
формул, выводимых в  . Проверим, что все теоремы
. Проверим, что все теоремы  выводятся
из
выводятся
из  . Пусть какая-то формула
. Пусть какая-то формула  выводится
из
выводится
из  , но не из
, но не из  . Тогда теория
. Тогда теория 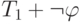 непротиворечива и по теореме 71 найдется (нормальная) модель
теории
непротиворечива и по теореме 71 найдется (нормальная) модель
теории  и ее расширение, являющееся моделью
теории
и ее расширение, являющееся моделью
теории  , что противоречит предположению.
, что противоречит предположению.
150. Докажите, что если формула устойчива относительно перехода к
подструктурам, то она выводимо эквивалентна  -формуле той
же сигнатуры.
-формуле той
же сигнатуры.
Симметричное рассуждение доказывает симметричное утверждение про 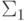 -аксиоматизируемые теории.
-аксиоматизируемые теории.
