НОУ ИНТУИТ | Языки и исчисления. Лекция 7: Арифметика Пресбургера

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 24.04.2007 | Доступ: свободный | Студентов: 722 / 35 | Оценка: 4.60 / 4.30 | Длительность: 25:56:00

Тема: Алгоритмы и дискретные структуры

Специальности: Программист

|

Вам нравится? Нравится 11 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Аннотация: Рассматриваются вопросы выразимости множеств для сигнатуры вида {=, <, +, 0, 1} и носителя Z, критерии существования бескванторных эквивалентных формул, вопросы элементарной эквивалентности

Ключевые слова: множества, предикатный символ, равенство, ПО, индекс, предикат, преобразования формул, линейная комбинация, свободными членами, целое число, коэффициенты, модуль, значение, объединение, размер шага, константы, сложение, отношение порядка, операции, дизъюнктивная нормальная форма, операция объединения, квантор существования, эквивалентные формулы, многочлен, таблица, числовая ось, прямой, диаграмма, пространство, истинность формул, старший коэффициент, остаток, деление, определение, максимальная степень, разбиение, информация, минимум, интервал, доказательство, действительное число, комплексное число, кратность, производные, поле, определитель, выражение, сигнатура, изоморфизм, взаимно однозначное отображение, отображение, композиция, отношение, отношение эквивалентности, обобщение, запись, интерпретация, эквивалентность, мощность, одноместная функция, место

Арифметика Пресбургера

В этом разделе мы описываем выразимые множества в $(\mathbb{Z},{=},{<},{+},0,1)$ . Отметим сразу же, что с такой сигнатурой элиминация кванторов невозможна. В самом деле, формула $\exists y\, (x\hm={y+y})$ , истинная для четных , не эквивалентна никакой бескванторной формуле. Поэтому нам нужно, прежде чем проводить элиминацию кванторов, расширить сигнатуру. Приведенный пример формулы подсказывает, какое расширение нам необходимо. 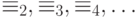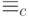Рассмотрим счетное семейство двуместных предикатных символов $\equiv_2, \equiv_3,\equiv_4,\dots$ Символ $\equiv_c$ будет интерпретироваться как равенство по модулю . 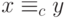Другими словами, формула $x\equiv_c y$ будет истинна в нашей интерпретации, если сравнимо с по модулю (остатки по модулю равны; x-y кратно ).

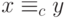Важно иметь в виду, что индекс в $x\equiv_c y$ не является переменной: у нас не трехместный предикат, а счетное семейство двуместных предикатов.

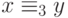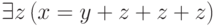Такое расширение не меняет класса выразимых предикатов, поскольку, например, $x\equiv_3 y$ можно выразить как $\exists z\, (x=y+z+z+z)$ . Зато после этого всякая формула эквивалентна бескванторной, как показывает следующая теорема (называемая теоремой об элиминации кванторов в арифметике Пресбургера).

Теорема 32. В 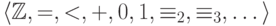$\langle\bbZ,=,<,+,0,1,\equiv_2,\equiv_3,\dots\rangle$ выполнима элиминация кванторов.

Мы будем применять метод, опробованный в предыдущем разделе: выбор представительного множества термов (после некоторых преобразований формулы).

Напомним, как это делается. Мы хотим доказать, что всякая формула эквивалентна бескванторной. Рассуждая по индукции, мы должны лишь проверить, что всякая формула вида

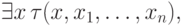
$\exists x\, \tau(x,x_1,\dots,x_n),$

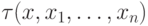где $\tau(x,x_1,\dots,x_n)$ обозначает бескванторную формулу, все переменные которой содержатся среди $x,x_1,\dots,x_n$ , эквивалентна некоторой бескванторной формуле (с теми же переменными, не считая

).

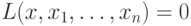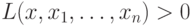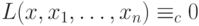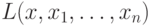Посмотрим, какие атомарные формулы, содержащие переменную , входят в $\tau$ . Перенося члены в одну сторону, эти атомарные формулы можно записать в одном из трех видов: $L(x,x_1,\dots,x_n)\hm=0$ , $L(x,x_1,\dots,x_n)\hm>0$ или $L(x,x_1,\dots,x_n)\hm\equiv_c 0$ , где $L(x,x_1,\dots,x_n)$ представляет собой линейную комбинацию переменных $x,x_1,\dots,x_n$ с целыми коэффициентами и целочисленным свободным членом. (В отличие от ситуации в $\mathbb{Q}$ , здесь нельзя делить на коэффициент при .) Перенося в левую часть, а все остальное — в правую, получаем соотношение одного из четырех видов:

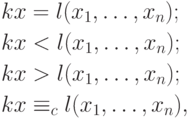
$\begin{align*} kx & = l(x_1,\dots,x_n);\\ kx & < l(x_1,\dots,x_n);\\ kx & > l(x_1,\dots,x_n);\\ kx & \equiv_c l(x_1,\dots,x_n), \end{align*}$

где

— положительное целое число (разное для разных атомарных формул), а

— линейная комбинация переменных $x_1,\dots,x_n$ с целыми коэффициентами и свободным членом.

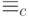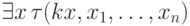Как мы говорили, коэффициенты в левой части (а также, разумеется, правые части) у разных атомарных формул разные. Однако мы можем их унифицировать, перейдя к общему кратному. В самом деле, неравенства и равенства можно умножать на число, сравнения — тоже, если модуль сравнения (индекс в $\equiv_c$ ) умножить на то же самое число. Поэтому можно считать, что наша формула имеет вид $\exists x\,\tau(kx,x_1,\dots,x_n)$ , понимая под этим, что появляется только в левых частях и везде с коэффициентом . Такую формулу можно переписать как

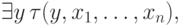
$\exists y\, (\tau(y,x_1,\dots,x_n) \land (y\equiv_k 0)).$

Таким образом, без ограничения общности можно считать, что k=1

, поскольку новая формула имеет тот же самый вид

$\exists y\, \tau(y,x_1,\dots,x_n),$

что и исходная, но уже безо всякого коэффициента при

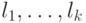(и с модифицированной формулой $\tau$ ). Пусть $l_1,\dots,l_k$ — выражения, стоящие в правых частях равенств, неравенств и сравнений с левой частью

.

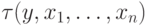Мы хотим, как и в предыдущем разделе, указать представительный набор значений $Y_1,\dots,Y_N$ . Каждое из Y_i представляет собой линейную комбинацию переменных $x_1,\dots,x_n$ с целыми коэффициентами и свободным членом. "Представительность" означает, что если для каких-то $x_1,\dots,x_n$ найдется , для которого $\tau(y,x_1,\dots,x_n)$ , то такой можно найти и среди значений $Y_1,\dots,Y_N$ (при тех же $x_1,\dots,x_n$ ).

Чтобы указать представительный набор, разделим все атомарные формулы в $\tau$ , содержащие , на два типа — сравнения по модулю и остальные (равенства и неравенства). Посмотрим, по каким модулям проводятся сравнения. Пусть — общее кратное всех этих модулей. В этом случае изменение значения переменной на величину, кратную , не влияет на результаты сравнений. Теперь возьмем все выражения, встречающиеся в правых частях равенств или неравенств, и будем прибавлять к ним всевозможные целые числа из отрезка от 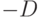до . Это и будет представительный набор. Другими словами, в представительный набор входят все выражения l+c , где — одна из правых частей равенств или неравенств, содержащих в левой части, а — целое число, не превосходящее по абсолютной величине.

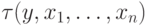Покажем, что полученный набор действительно будет представительным. Пусть при данных $x_1,\dots,x_n$ найдется некоторое , для которого $\tau(y,x_1,\dots,x_n)$ . Посмотрим, какие значения принимают правые части равенств и неравенств при данных $x_1,\dots,x_n$ . Если значение попало в объединение -окрестностей этих значений, то доказывать нечего. Если же нет, начнем смещать , двигаясь шагами размера в направлении какой-то точки из этого объединения. Миновать мы ее не можем (ширина окрестности равна , а размер шага равен ), поэтому в какой-то момент мы впервые попадем в это объединение. Обозначим эту точку (первую попавшую в объединение) через 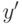. Тогда 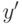при подстановке в $\tau$ дает те же самые результаты, что и . В самом деле, для сравнений это гарантировано, потому что сдвиг кратен модулю сравнений. Но это верно и для равенств и неравенств, поскольку на предыдущем шаге мы были вне -окрестности всех правых частей и потому не могли перейти с одной стороны на другую.

Таким образом, среди представительного набора есть значение (а именно, 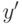), удовлетворяющее формуле $\tau$ , что и требовалось доказать.

Итак, мы получили ответ на интересующий нас вопрос: выразимые в арифметике Пресбургера предикаты — это предикаты, выразимые бескванторными формулами, содержащими целые константы, сложение, равенство, отношение порядка и сравнения по любым фиксированным модулям.

Дальше >>

Авторизоваться

Языки и исчисления

Арифметика Пресбургера

Арифметика Пресбургера

Вопросы и ответы