Арифметика Пресбургера
Пример. Выпишем диаграмму
для системы многочленов 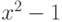 ,
,  ,
,  .
Корнями здесь будут числа
.
Корнями здесь будут числа 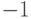 ,
,  ,
,  , так что столбцы соответствуют
четырем промежуткам и трем разделяющим их корням.
, так что столбцы соответствуют
четырем промежуткам и трем разделяющим их корням.
![\begin{array}{r|ccccccc}
\mathstrut& & \langle -1\rangle & & \langle 0\rangle & &
\langle 1\rangle & \\[0.2ex]
\hline\\[-2.3ex]
x^2-1\mathstrut & + & 0 & - & - & - & 0 & +\\
x & - & - & - & 0 & + & + & +\\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0
\end{array}](/sites/default/files/tex_cache/a2ec5ea895e0f1f5514894644110ea36.png)
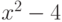 ,
,  ,
,  имеет точно такую же диаграмму.
имеет точно такую же диаграмму.Если ни один из многочленов не имеет корней, то они сохраняют знак на всей прямой, и диаграмма состоит из единственного столбца, в котором записаны все эти знаки.
Теперь рассмотрим набор многочленов ![Q_1,\dots,Q_k\hm\in\mathbb Z[x,x_1,\dots,x_n]](/sites/default/files/tex_cache/f9c3bcbd8445381d861a01da1e32b699.png) . При фиксированных
значениях переменных
. При фиксированных
значениях переменных  мы получаем набор
многочленов от одной переменной с действительными коэффициентами
и можем построить его диаграмму. Эта диаграмма будет зависеть от
выбора значений
мы получаем набор
многочленов от одной переменной с действительными коэффициентами
и можем построить его диаграмму. Эта диаграмма будет зависеть от
выбора значений  . Число строк в диаграмме равно
. Число строк в диаграмме равно  , а ширина ее зависит от числа различных корней и может
меняться, однако во всех случаях не превосходит
, а ширина ее зависит от числа различных корней и может
меняться, однако во всех случаях не превосходит 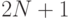 , где
, где  — сумма степеней всех многочленов (рассматриваются степени
по
— сумма степеней всех многочленов (рассматриваются степени
по  , то есть степени соответствующих многочленов от
, то есть степени соответствующих многочленов от  с коэффициентами в
с коэффициентами в ![\mathbb Z[x_1,\dots,x_n]](/sites/default/files/tex_cache/c757a56015586cc29fdc19aa7dd59dee.png) ).
).
Таким образом, число возможных диаграмм конечно, и пространство 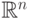 возможных значений переменных
возможных значений переменных  разбивается на конечное число частей: каждая часть соответствует
одному из возможных значений диаграммы.
разбивается на конечное число частей: каждая часть соответствует
одному из возможных значений диаграммы.
Для доказательства теоремы Тарского-Зайденберга достаточно
доказать, что эти части будут полуалгебраическими множествами.
В самом деле, если в качестве многочленов 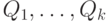 взять многочлены, входящие в формулу
взять многочлены, входящие в формулу 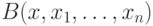 ,
то область истинности формулы
,
то область истинности формулы

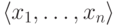 в пределах одной части разбиения, то диаграмма не меняется, значит,
и истинность формулы
в пределах одной части разбиения, то диаграмма не меняется, значит,
и истинность формулы  не меняется (по диаграмме можно
определить истинность формулы, перепробовав значения
не меняется (по диаграмме можно
определить истинность формулы, перепробовав значения  ,
соответствующие всем столбцам).
,
соответствующие всем столбцам).Итак, нам осталось доказать, что для любого набора
многочленов ![Q_1,\dots,Q_k\hm\in\mathbb Z[x,x_1,\dots,x_n]](/sites/default/files/tex_cache/f9c3bcbd8445381d861a01da1e32b699.png) части
пространства
части
пространства 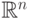 , соответствующие различным значениям
диаграммы, являются полуалгебраическими множествами.
Начнем с такого очевидного наблюдения: если это верно для
какого-то набора
, соответствующие различным значениям
диаграммы, являются полуалгебраическими множествами.
Начнем с такого очевидного наблюдения: если это верно для
какого-то набора 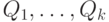 , то это останется верным
и для любого меньшего набора. В самом деле, диаграмму
меньшего семейства многочленов можно получить из диаграммы
большего семейства: выкидывая многочлен, надо выбросить
соответствующую строку, а также столбцы, которые соответствовали
корням этого многочлена (если они не были корнями других
многочленов). При выбрасывании столбца два окружающих его
столбца сливаются в один.
, то это останется верным
и для любого меньшего набора. В самом деле, диаграмму
меньшего семейства многочленов можно получить из диаграммы
большего семейства: выкидывая многочлен, надо выбросить
соответствующую строку, а также столбцы, которые соответствовали
корням этого многочлена (если они не были корнями других
многочленов). При выбрасывании столбца два окружающих его
столбца сливаются в один.
Поэтому мы имеем право для удобства расширить данный нам набор многочленов и доказывать полуалгебраичность частей для расширенного набора. Расширение будет состоять в замыкании относительно некоторых операций, которые мы сейчас опишем.
Напомним еще раз, что мы рассматриваем семейство многочленов
из ![\mathbb Z[x,x_1,\dots,x_n]](/sites/default/files/tex_cache/420eb44c65de5b2ba34dd8fdd1f0897e.png) , которые разложены по степеням
, которые разложены по степеням  , то есть записаны как многочлены от
, то есть записаны как многочлены от  с коэффициентами в
с коэффициентами в ![\mathbb Z[x_1,\dots,x_k]](/sites/default/files/tex_cache/8d1a3837bfd0f776b9ebb30d75affa7f.png) . Рассмотрим следующие операции:
. Рассмотрим следующие операции:
- отбрасывание старшего члена (с наибольшей степенью
переменной
 ); эта операция понижает степень (по
); эта операция понижает степень (по  ) на
единицу;
) на
единицу; - взятие старшего коэффициента (коэффициента при наибольшей
степени переменной
 ); эта операция понижает степень (по
); эта операция понижает степень (по  ) до нуля;
) до нуля; - дифференцирование по
 ; эта операция понижает степень (по
; эта операция понижает степень (по  ) на единицу;
) на единицу; - взятие модифицированного остатка при делении одного многочлена на другой.
Говоря о "модифицированном остатке", мы имеем в виду следующее. При делении "уголком"
многочлена  на многочлен
на многочлен  с
остатком нам неоднократно приходится делить на старший
коэффициент многочлена
с
остатком нам неоднократно приходится делить на старший
коэффициент многочлена  . Поэтому в общем случае коэффициенты
частного и остатка представляют собой дроби, в знаменателях
которых стоят некоторые степени старшего коэффициента многочлена
. Поэтому в общем случае коэффициенты
частного и остатка представляют собой дроби, в знаменателях
которых стоят некоторые степени старшего коэффициента многочлена  .
.
Тем самым при вычислении остатка от деления  на
на  мы выходим за пределы кольца
мы выходим за пределы кольца ![\mathbb Z[x,x_1,\dots,x_n]](/sites/default/files/tex_cache/420eb44c65de5b2ba34dd8fdd1f0897e.png) . Этого не
случится, если старший коэффициент многочлена
. Этого не
случится, если старший коэффициент многочлена  равен единице.
Но в общем случае мы должны принять какие-то меры, если хотим
оставаться в указанном кольце. Меры эти состоят в следующем:
прежде чем делить
равен единице.
Но в общем случае мы должны принять какие-то меры, если хотим
оставаться в указанном кольце. Меры эти состоят в следующем:
прежде чем делить  на
на  , мы умножаем
, мы умножаем  на старший коэффициент многочлена
на старший коэффициент многочлена  в достаточно большой степени. Если
вспомнить процедуру деления уголком, легко сообразить, что
достаточно взять степень
в достаточно большой степени. Если
вспомнить процедуру деления уголком, легко сообразить, что
достаточно взять степень  , где
, где  и
и  — степени многочленов
— степени многочленов  и
и  (по переменной
(по переменной  ).
Например, при
).
Например, при 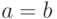 требуется всего один
шаг деления, и достаточно умножить
требуется всего один
шаг деления, и достаточно умножить  на старший коэффициент
многочлена
на старший коэффициент
многочлена  в первой степени.
в первой степени.
Итак, операция модифицированного остатка применима к любым двум
многочленам ![A,B\hm\in(\mathbb Z[x_1,\dots,x_n])[x]](/sites/default/files/tex_cache/79c996ab5dd1af326b1d97b83eec4dea.png) степеней
степеней  и
и  (по
(по  ) и дает третий многочлен этого кольца,
который есть остаток от деления
) и дает третий многочлен этого кольца,
который есть остаток от деления 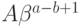 на
на  (здесь
(здесь  — старший коэффициент многочлена
— старший коэффициент многочлена  ). Заметим, что степень этого
многочлена меньше степени многочлена
). Заметим, что степень этого
многочлена меньше степени многочлена  . Мы будем предполагать,
что
. Мы будем предполагать,
что  (иначе остаток совпадает с
(иначе остаток совпадает с  и деление не
дает ничего нового). Таким образом, результат этой операции имеет
меньшую степень, чем оба операнда.
и деление не
дает ничего нового). Таким образом, результат этой операции имеет
меньшую степень, чем оба операнда.
Заметим, что определение модифицированного остатка
имеет смысл для многочленов с коэффициентами из произвольного
кольца (не только ![\mathbb Z[x_1,\dots,x_n]](/sites/default/files/tex_cache/c757a56015586cc29fdc19aa7dd59dee.png) ).
).
Лемма 1. Для всякого конечного множества  многочленов из
многочленов из ![(\mathbb Z[x_1,\dots,x_n])[x]](/sites/default/files/tex_cache/e4fce03bc9d22fa974664510e9e65884.png) существует его
конечное расширение, замкнутое относительно указанных четырех
операций.
существует его
конечное расширение, замкнутое относительно указанных четырех
операций.
Это утверждение верно для любого кольца
коэффициентов и почти очевидно следует из
того, что степень результата операции меньше степени (любого)
операнда. Более формально рассуждать надо так. Рассмотрим
выражения, составленные из элементов  с помощью четырех
указанных операций. Глубина такого выражения не превосходит
максимальной степени многочленов из
с помощью четырех
указанных операций. Глубина такого выражения не превосходит
максимальной степени многочленов из  , поскольку каждая
операция уменьшает степень. Поэтому таких выражений конечное
число, и их множество очевидным образом замкнуто относительно
указанных операций. Лемма 1 доказана.
, поскольку каждая
операция уменьшает степень. Поэтому таких выражений конечное
число, и их множество очевидным образом замкнуто относительно
указанных операций. Лемма 1 доказана.
Доказанная лемма позволяет без ограничения общности считать, что данное нам конечное множество многочленов замкнуто относительно четырех указанных выше операций.
