Теории и модели
Аксиомы равенства
Пусть сигнатура  включает в себя двуместный предикат
равенства (записываемый традиционно
включает в себя двуместный предикат
равенства (записываемый традиционно 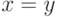 ). Интерпретация этой
сигнатуры называется нормальной,если предикат равенства
интерпретируется как тождественное совпадение элементов носителя.
). Интерпретация этой
сигнатуры называется нормальной,если предикат равенства
интерпретируется как тождественное совпадение элементов носителя.
Возникает естественный вопрос. Пусть имеется некоторая
теория  (множество замкнутых формул) в языке, сигнатура
которого включает равенство. Мы знаем что теория имеет модель
(интерпретацию, в которой все формулы из
(множество замкнутых формул) в языке, сигнатура
которого включает равенство. Мы знаем что теория имеет модель
(интерпретацию, в которой все формулы из  истинны) тогда и
только тогда, когда она непротиворечива. В каком случае она
имеет нормальную модель (нормальную интерпретацию, в которой все
формулы из
истинны) тогда и
только тогда, когда она непротиворечива. В каком случае она
имеет нормальную модель (нормальную интерпретацию, в которой все
формулы из  истинны)?
истинны)?
Чтобы ответить на этот вопрос, введем аксиомы равенства. Пусть  произвольная сигнатура. Аксиомами равенства
в сигнатуре
произвольная сигнатура. Аксиомами равенства
в сигнатуре  будут формулы
будут формулы
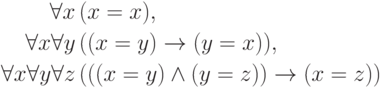
 соответствующая аксиома выглядит так:
соответствующая аксиома выглядит так: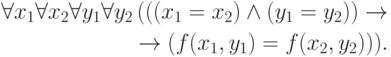
 аксиома
такова:
аксиома
такова: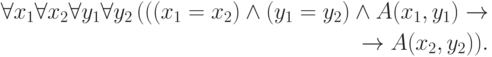
Теорема 59 (полноты для нормальных моделей).
Теория  сигнатуры
сигнатуры  с равенством имеет
нормальную модель тогда и только тогда, когда она остается непротиворечивой
при добавлении аксиом равенства.
с равенством имеет
нормальную модель тогда и только тогда, когда она остается непротиворечивой
при добавлении аксиом равенства.
Прежде всего заметим, что теоремы о корректности и полноте (раздел "Полнота исчисления предикатов") позволяют говорить о совместности вместо непротиворечивости.
В нормальной модели теории  аксиомы равенства
истинны, так что в одну сторону утверждение теоремы очевидно.
Нам осталось показать, что если теория
аксиомы равенства
истинны, так что в одну сторону утверждение теоремы очевидно.
Нам осталось показать, что если теория  совместна с аксиомами
равенства, то она имеет нормальную модель.
совместна с аксиомами
равенства, то она имеет нормальную модель.
Возьмем произвольную интерпретацию, в которой истинны формулы
из  и аксиомы равенства. Пусть
и аксиомы равенства. Пусть  — ее носитель. В
этой интерпретации предикат
— ее носитель. В
этой интерпретации предикат  не обязан быть настоящим равенством;
он представляет собой некоторое бинарное отношение на
не обязан быть настоящим равенством;
он представляет собой некоторое бинарное отношение на  .
Поскольку выполнены аксиомы равенства, это отношение
рефлексивно, симметрично и транзитивно (является отношением
эквивалентности). Следовательно, множество
.
Поскольку выполнены аксиомы равенства, это отношение
рефлексивно, симметрично и транзитивно (является отношением
эквивалентности). Следовательно, множество  разбивается на
классы эквивалентности; множество этих классов обозначим
разбивается на
классы эквивалентности; множество этих классов обозначим 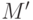 (его можно назвать фактор-множеством
(его можно назвать фактор-множеством  по данному отношению
эквивалентности). Класс элемента
по данному отношению
эквивалентности). Класс элемента  будем обозначать
будем обозначать ![[x]](/sites/default/files/tex_cache/3e5314e9fd31509fdeb83faa0f729ba2.png) .
.
Аксиомы равенства позволяют корректно определить интерпретацию c
носителем 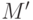 . В самом деле, истинность аксиомы для
функционального символа
. В самом деле, истинность аксиомы для
функционального символа  (приведенной выше в качестве
примера) гарантирует, что класс
(приведенной выше в качестве
примера) гарантирует, что класс ![[f(x,y)]](/sites/default/files/tex_cache/b0d85b3e81039b866b54a1f5f3b18211.png) зависит лишь от
классов
зависит лишь от
классов ![[x]](/sites/default/files/tex_cache/3e5314e9fd31509fdeb83faa0f729ba2.png) и
и ![[y]](/sites/default/files/tex_cache/eff269c75e4be2dbf92c0368320fda54.png) , но не от выбора
, но не от выбора  и
и  внутри класса. Аналогичным образом аксиомы для предикатных символов позволяют
корректно определить предикаты на классах.
внутри класса. Аналогичным образом аксиомы для предикатных символов позволяют
корректно определить предикаты на классах.
Полученная интерпретация с носителем 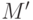 по построению
нормальна. Осталось убедиться, что в ней истинны те же самые
формулы, что и в
по построению
нормальна. Осталось убедиться, что в ней истинны те же самые
формулы, что и в  (в том числе все формулы
теории
(в том числе все формулы
теории  ). Это почти очевидно с интуитивной точки зрения:
). Это почти очевидно с интуитивной точки зрения:  отличается
от
отличается
от 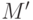 лишь тем, что каждый элемент представлен несколькими
равноправными копиями, которые со всех точек зрения ведут себя
одинаково.
лишь тем, что каждый элемент представлен несколькими
равноправными копиями, которые со всех точек зрения ведут себя
одинаково.
Формально говоря, мы доказываем, что формула  истинна в
интерпретации
истинна в
интерпретации  на оценке
на оценке  тогда и только тогда,
когда
тогда и только тогда,
когда  истинна в
истинна в 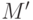 на оценке
на оценке 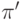 ,
при которой значение любой переменной
,
при которой значение любой переменной  есть класс, содержащий значение
переменной
есть класс, содержащий значение
переменной  при оценке
при оценке  . Это легко сделать
индукцией по построению формулы
. Это легко сделать
индукцией по построению формулы  .
.
111. Покажите, что из аксиом равенства для сигнатуры  выводится формула
выводится формула
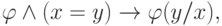
 .)
.)112. Покажите, что если теория  (не обязательно с равенством)
имеет модель мощности
(не обязательно с равенством)
имеет модель мощности  , то она имеет и модель
любой большей мощности. (Указание: элементы модели можно
"клонировать" в произвольном количестве.)
, то она имеет и модель
любой большей мощности. (Указание: элементы модели можно
"клонировать" в произвольном количестве.)
Из теоремы о полноте для нормальных моделей легко следует аналог теоремы о компактности (теорема 50) для нормальных моделей.
Теорема 60 (компактности для нормальных моделей).
Если всякое конечное подмножество теории  в сигнатуре
с равенством имеет нормальную модель, то и теория
в сигнатуре
с равенством имеет нормальную модель, то и теория  имеет нормальную модель.
имеет нормальную модель.
Любое конечное подмножество теории  остается непротиворечивым
при добавлении аксиом равенства (поскольку имеет нормальную модель).
Значит, и вся теория
остается непротиворечивым
при добавлении аксиом равенства (поскольку имеет нормальную модель).
Значит, и вся теория  остается непротиворечивой при
добавлении аксиом равенства (вывод противоречия использует
конечное число формул) и потому имеет нормальную модель.
остается непротиворечивой при
добавлении аксиом равенства (вывод противоречия использует
конечное число формул) и потому имеет нормальную модель.
113. Применив теорему о компактности, докажите, что всякий частичный порядок может быть продолжен до линейного. (Указание. Рассмотрим частично упорядоченное множество как модель теории, в сигнатуре которой есть равенство, порядок и константы для всех элементов множества, а формулами являются равенства и неравенства между константами. Добавим к ней утверждение о сравнимости любых двух элементов. Покажите, что любое конечное множество формул полученной теории непротиворечиво, используя тот факт, что частичный порядок на конечном множестве продолжается до линейного.)
114. Используя теорему о компактности, докажите, что для всякого поля  сушествует его расширение
сушествует его расширение 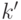 , в котором всякий
многочлен с коэффициентами из
, в котором всякий
многочлен с коэффициентами из  имеет корень. (Указание. Утверждение о
существовании корня у многочлена с данными коэффициентами можно
записать в виде формулы. Любое конечное множество таких формул
совместно с аксиомами поля, так как можно по очереди
присоединить корни соответствующих многочленов.)
имеет корень. (Указание. Утверждение о
существовании корня у многочлена с данными коэффициентами можно
записать в виде формулы. Любое конечное множество таких формул
совместно с аксиомами поля, так как можно по очереди
присоединить корни соответствующих многочленов.)
115. Пусть  — множество замкнутых формул в сигнатуре с
равенством. Покажите, что замкнутая формула
— множество замкнутых формул в сигнатуре с
равенством. Покажите, что замкнутая формула  этой
сигнатуры истинна во всех нормальных моделях
этой
сигнатуры истинна во всех нормальных моделях  тогда и
только тогда, когда она выводима из
тогда и
только тогда, когда она выводима из  и аксиом равенства.
и аксиом равенства.
Утверждение последней задачи является аналогом
теоремы 51 для теорий с равенством.
Иногда вообще рассматривают только такие теории. При этом
равенство является обязательным элементом сигнатуры, аксиомы
равенства (их число зависит от сигнатуры) считаются частью
исчисления предикатов, а интерпретации рассматриваются только
нормальные. При этом теория имеет [нормальную] модель тогда и
только тогда, когда она непротиворечива [вместе с аксиомами
равенства]; формула выводима из теории  [и аксиом
равенства] тогда и только тогда, когда она верна во всех
[нормальных] моделях теории
[и аксиом
равенства] тогда и только тогда, когда она верна во всех
[нормальных] моделях теории  и т. п. (в квадратных скобках
указаны подразумеваемые слова).
и т. п. (в квадратных скобках
указаны подразумеваемые слова).
