Теории и модели
Повышение мощности
Теорема Левенгейма-Сколема позволяла уменьшать мощность интерпретации (она утверждала, что для любой бесконечной интерпретации конечной или счетной сигнатуры существует элементарно эквивалентная ей счетная подструктура). В этом разделе мы рассмотрим обратную задачу — расширение интерпретации до элементарно эквивалентной интерпретации большей мощности. Соответствующее утверждение также называют теоремой Левенгейма-Сколема.
Прежде всего отметим, что без требования нормальности это утверждение бессодержательно: как уже говорилось, мы можем дублировать элементы сигнатуры в произвольном количестве. Поэтому мы предполагаем, что все рассматриваемые интерпретации нормальны (равенство интерпретируется как тождественное совпадение).
Теорема 61 (Левенгейма-Сколема о повышении мощности).
Пусть  — бесконечная нормальная интерпретация некоторой
сигнатуры
— бесконечная нормальная интерпретация некоторой
сигнатуры  с равенством. Тогда существует нормальная
интерпретация
с равенством. Тогда существует нормальная
интерпретация 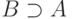 сколь угодно большой мощности,
являющаяся элементарным расширением
сколь угодно большой мощности,
являющаяся элементарным расширением  .
.
(Это означает, согласно определению, напомним, что интерпретация
предикатных и функциональных символов в  продолжает их
интерпретацию в
продолжает их
интерпретацию в  и что формулы сигнатуры
и что формулы сигнатуры  ,
параметрам которых приданы значения из
,
параметрам которых приданы значения из  , одновременно истинны
в
, одновременно истинны
в  и в
и в  .)
.)
Сформулируем утверждение теоремы в терминах теорий и моделей.
Пусть  — произвольная нормальная интерпретация
сигнатуры
— произвольная нормальная интерпретация
сигнатуры  . Рассмотрим сигнатуру
. Рассмотрим сигнатуру 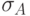 ,
которая получается из
,
которая получается из  добавлением констант — по одной для
каждого элемента множества
добавлением констант — по одной для
каждого элемента множества  . Эта сигнатура имеет естественную
нормальную интерпретацию с носителем
. Эта сигнатура имеет естественную
нормальную интерпретацию с носителем  : значением каждой
константы является соответствующий ей элемент. (Возможно, что в
: значением каждой
константы является соответствующий ей элемент. (Возможно, что в  изначально было достаточно констант и всякий
элемент
изначально было достаточно констант и всякий
элемент  был значением некоторой константы. Тогда эта
процедура лишняя, но и вреда от нее нет.)
был значением некоторой константы. Тогда эта
процедура лишняя, но и вреда от нее нет.)
Рассмотрим теорию  , состоящую из формул
сигнатуры
, состоящую из формул
сигнатуры 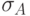 , истинных в
, истинных в  при указанной
интерпретации. Всякое элементарное расширение
при указанной
интерпретации. Всякое элементарное расширение  интерпретации
интерпретации  будет моделью теории
будет моделью теории  . В
самом деле, замкнутая формула
. В
самом деле, замкнутая формула 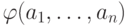 сигнатуры
сигнатуры 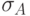 получается подстановкой констант
получается подстановкой констант 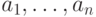 вместо
параметров из какой-то формулы
вместо
параметров из какой-то формулы 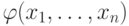 сигнатуры
сигнатуры  . (Мы
используем не вполне корректные обозначения, в частности, отождествляем
элементы
. (Мы
используем не вполне корректные обозначения, в частности, отождествляем
элементы 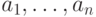 множества
множества  с константами для
них.) Ее истинность в
с константами для
них.) Ее истинность в  (или в
(или в  ) равносильна истинности
формулы
) равносильна истинности
формулы 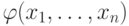 при значениях параметров
при значениях параметров 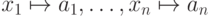 — формально говоря,
следует воспользоваться леммой 2. Поэтому по определению элементарного расширения все формулы
из
— формально говоря,
следует воспользоваться леммой 2. Поэтому по определению элементарного расширения все формулы
из  будут истинны и в
будут истинны и в  .
.
Верно и обратное: любая нормальная модель теории  естественно
определяет элементарное расширение интерпретации
естественно
определяет элементарное расширение интерпретации  . В самом
деле, пусть дана нормальная модель этой теории с носителем
. В самом
деле, пусть дана нормальная модель этой теории с носителем  .
Тогда каждый элемент множества
.
Тогда каждый элемент множества  (точнее, соответствующая этому элементу константа)
интерпретируется некоторым элементом множества
(точнее, соответствующая этому элементу константа)
интерпретируется некоторым элементом множества  . Разным элементам
множества
. Разным элементам
множества  соответствуют разные элементы в
соответствуют разные элементы в  , так как формула
, так как формула 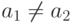 , истинная в
, истинная в  , должна быть истинной и
в
, должна быть истинной и
в  . Таким образом,
. Таким образом,  вкладывается в
вкладывается в  и можно отождествить его
с некоторым подмножеством множества
и можно отождествить его
с некоторым подмножеством множества  . Это отождествление
корректно в том смысле, что предикаты и функциональные символы
интерпретируются согласованным образом. В самом деле, атомарные
формулы вида
. Это отождествление
корректно в том смысле, что предикаты и функциональные символы
интерпретируются согласованным образом. В самом деле, атомарные
формулы вида  , а также формулы
, а также формулы 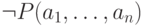 и
и 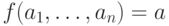 , истинные в
, истинные в  , истинны и в
, истинны и в  . Истинные в
. Истинные в  формулы вида
формулы вида 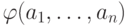 принадлежат
принадлежат  и потому
истинны и в
и потому
истинны и в  ; ложные в
; ложные в  формулы имеют отрицания в
формулы имеют отрицания в  и потому ложны в
и потому ложны в  .
.
Таким образом, для доказательства теоремы Левенгейма-Сколема о
повышении мощности осталось построить нормальную модель теории  , имеющую сколь угодно большую мощность. Это можно
сделать так: добавим множество новых констант
, имеющую сколь угодно большую мощность. Это можно
сделать так: добавим множество новых констант 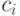 и формулы
и формулы 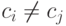 (для всех
(для всех 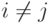 ) к теории
) к теории  . Полученная теория будет совместной по теореме компактности для
нормальных моделей. (В самом деле, любая конечная часть ее имеет
нормальную модель, поскольку содержит конечное число новых
констант, и им можно придать различные значения в
. Полученная теория будет совместной по теореме компактности для
нормальных моделей. (В самом деле, любая конечная часть ее имеет
нормальную модель, поскольку содержит конечное число новых
констант, и им можно придать различные значения в  .) Поэтому
и вся теория имеет нормальную модель. Всем константам
.) Поэтому
и вся теория имеет нормальную модель. Всем константам 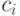 соответствуют в этой модели разные элементы (поскольку истинна
формула
соответствуют в этой модели разные элементы (поскольку истинна
формула 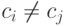 ), поэтому мощность этой модели может
быть сколь угодно большой, если использовать достаточно много
констант.
), поэтому мощность этой модели может
быть сколь угодно большой, если использовать достаточно много
констант.
Этот же прием будет использован нами при построении нестандартной модели арифметики
Приведенное рассуждение дает оценку мощности снизу. Можно получить и в точности нужную мощность:
