Теорема Эрбрана
Предваренная нормальная форма
Говорят, что формула находится в предваренной нормальной форме, если все кванторы в ней вынесены налево, то есть если она имеет вид
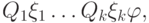
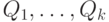 — кванторы всеобщности или существования,
— кванторы всеобщности или существования, 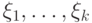 — переменные, а
— переменные, а  —
бескванторная формула. Эта формула может иметь параметры (если
формула
—
бескванторная формула. Эта формула может иметь параметры (если
формула  имеет параметры, отличные от
имеет параметры, отличные от 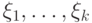 ).
).Основной результат этого раздела гласит, что всякая формула (доказуемо) эквивалентна некоторой формуле в предваренной нормальной форме (предваренной формуле). Мы докажем его, одновременно построив некоторую классификацию формул (в каком- то смысле отражающую их "логическую сложность"). В качестве меры сложности можно было бы взять число кванторов в предваренной нормальной форме. Но правильнее учитывать число групп кванторов (считая одноименные рядом стоящие кванторы за один).
Говорят, что предваренная формула является  -
формулой, если ее кванторная приставка содержит
-
формулой, если ее кванторная приставка содержит  групп
кванторов, причем первыми стоят кванторы существования. Если
первыми стоят кванторы всеобщности, говорят о классе
групп
кванторов, причем первыми стоят кванторы существования. Если
первыми стоят кванторы всеобщности, говорят о классе 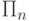 .
(Аналогичные обозначения используются в теории алгоритмов для
классификации арифметических множеств,
см. [5]).
.
(Аналогичные обозначения используются в теории алгоритмов для
классификации арифметических множеств,
см. [5]).
Пример: формула 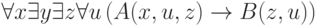 принадлежит классу
принадлежит классу 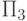 , формула
, формула  принадлежит
классу
принадлежит
классу 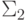 , а
формула
, а
формула  вообще не
находится в предваренной нормальной форме.
вообще не
находится в предваренной нормальной форме.
103. Указать формулу в предваренной нормальной форме, доказуемо эквивалентную последней из перечисленных формул.
Нас интересует, что происходит с измеряемой таким образом "логической сложностью" формулы при логических операциях. Начнем с совсем простых наблюдений.
- Всякая формула из класса
 или
или 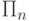 доказуемо эквивалентна формуле из класса
доказуемо эквивалентна формуле из класса  , а также формуле
из класса
, а также формуле
из класса 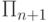 . В самом деле, если формула
. В самом деле, если формула  не имеет параметра
не имеет параметра 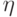 , то она будет доказуемо эквивалентна формулам
, то она будет доказуемо эквивалентна формулам 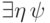 и
и 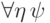 (одна
импликация является аксиомой, другая получается из
(одна
импликация является аксиомой, другая получается из  по
правилу Бернайса). Таким образом, можно добавить фиктивный
квантор в начало кванторной приставки или в ее конец; во втором
случае надо сослаться на лемму 2.
по
правилу Бернайса). Таким образом, можно добавить фиктивный
квантор в начало кванторной приставки или в ее конец; во втором
случае надо сослаться на лемму 2. - Отрицание любой формулы из класса
 доказуемо
эквивалентно некоторой формуле из класса
доказуемо
эквивалентно некоторой формуле из класса 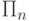 и наоборот. В
самом деле, мы видели, что
и наоборот. В
самом деле, мы видели, что  выводимо
эквивалентно
выводимо
эквивалентно 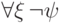 и наоборот, так что отрицание можно
проносить внутрь, меняя по ходу дела кванторы на двойственные.
и наоборот, так что отрицание можно
проносить внутрь, меняя по ходу дела кванторы на двойственные. -
Покажем, что конъюнкция двух формул из
 доказуемо
эквивалентна некоторой формуле из
доказуемо
эквивалентна некоторой формуле из  . Например,
конъюнкция
. Например,
конъюнкция 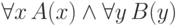 доказуемо эквивалентна формуле
доказуемо эквивалентна формуле  . В самом деле, используя аксиомы про квантор
всеобщности, можно из
. В самом деле, используя аксиомы про квантор
всеобщности, можно из 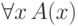 вывести
вывести 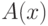 ,
а из
,
а из 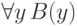 вывести
вывести 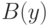 , поэтому из их
конъюнкции выводится
, поэтому из их
конъюнкции выводится  , после чего можно навесить два
квантора всеобщности. В другую сторону:
выводим формулу
, после чего можно навесить два
квантора всеобщности. В другую сторону:
выводим формулу  , затем применяем правило Бернайса и т. д.
, затем применяем правило Бернайса и т. д.104. Покажите, что можно сэкономить один квантор и использовать формулу
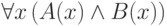 .
.Общее рассуждение (для любых двух формул из класса
 )
почти столь же просто, надо лишь переименовать связанные
переменные, пользуясь теоремой 52.
)
почти столь же просто, надо лишь переименовать связанные
переменные, пользуясь теоремой 52. - Аналогично можно доказать, что дизъюнкция двух формул
из класса
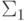 доказуемо эквивалентна некоторой формуле
класса
доказуемо эквивалентна некоторой формуле
класса 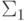 . (Можно также перейти к двойственному
классу
. (Можно также перейти к двойственному
классу  , воспользовавшись уже известными свойствами
отрицания.)
, воспользовавшись уже известными свойствами
отрицания.) -
Покажем теперь, что конъюнкция двух формул из класса
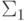 доказуемо эквивалентна формуле класса
доказуемо эквивалентна формуле класса 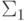 и что
дизъюнкция двух формул класса
и что
дизъюнкция двух формул класса  доказуемо эквивалентна
формуле класса
доказуемо эквивалентна
формуле класса  . Для этого надо воспользоваться
эквивалентностями видаи
. Для этого надо воспользоваться
эквивалентностями видаи Отметим кстати, что в них уже нельзя сэкономить квантор; например, формула
Отметим кстати, что в них уже нельзя сэкономить квантор; например, формула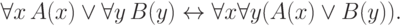
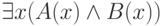 не равносильна
формуле
не равносильна
формуле 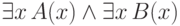 . (В одном из
выступлений времен начала перестройки М.С.Горбачев сказал, что нужны
"преданные делу социализма, но квалифицированные специалисты" —
впрочем, в газетной публикации "но" было заменено на
нейтральное "и". Так вот, их существование не вытекает из
отдельного существования тех и других.)
. (В одном из
выступлений времен начала перестройки М.С.Горбачев сказал, что нужны
"преданные делу социализма, но квалифицированные специалисты" —
впрочем, в газетной публикации "но" было заменено на
нейтральное "и". Так вот, их существование не вытекает из
отдельного существования тех и других.)
Указанные эквивалентности, как легко видеть, общезначимы и потому выводимы. Это совсем просто понять для первой из них (чтобы найти пару объектов с заданными свойствами, надо найти отдельно первый и второй члены пары). Вторая эквивалентность немного сложнее — проще всего заметить, что она переходит в первую при добавлении отрицания. (Большая сложность отражает тот факт, что вторая эквивалентность, в отличие от первой, не является интуиционистски верной.)
-
Теперь легко понять, что конъюнкция и дизъюнкция двух формул из класса
 (или
(или  доказуемо эквивалентны
формулам из того же класса. В самом деле, с помощью указанных
выше эквивалентностей можно слить кванторные приставки.
Например, формуладоказуемо эквивалентна сначала формуле
доказуемо эквивалентны
формулам из того же класса. В самом деле, с помощью указанных
выше эквивалентностей можно слить кванторные приставки.
Например, формуладоказуемо эквивалентна сначала формуле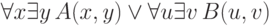 а затем формуле
а затем формуле
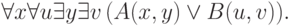
105. Как сэкономить один квантор в этом преобразовании?
Теперь все готово для доказательства упомянутого в начале раздела результата.
Теорема 53 (о предваренной нормальной форме). Любая формула произвольной сигнатуры доказуемо эквивалентна некоторой формуле той же сигнатуры, имеющей предваренную нормальную форму.
Индукция по построению формулы. Для атомарных формул это
очевидно. Отрицание переводит формулу класса  в
класс
в
класс 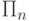 и наоборот. Конъюнкция и дизъюнкция: приведем
каждую формулу к предваренной нормальной форме, затем добавим
фиктивные кванторы так, чтобы они попали в один класс, а затем
воспользуемся доказанным утверждением. Импликация сводится к
дизъюнкции и отрицанию (
и наоборот. Конъюнкция и дизъюнкция: приведем
каждую формулу к предваренной нормальной форме, затем добавим
фиктивные кванторы так, чтобы они попали в один класс, а затем
воспользуемся доказанным утверждением. Импликация сводится к
дизъюнкции и отрицанию (  доказуемо
эквивалентно
доказуемо
эквивалентно 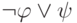 ).
).
Отметим, что ни формулировка, ни доказательство этой теоремы не предполагают замкнутости формулы.
106. Привести к предваренной нормальной форме формулу 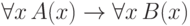 .
.
107. Формулы  и
и  принадлежат
классу
принадлежат
классу  . Найдем формулу в предваренной нормальной форме, выводимо
эквивалентную формуле
. Найдем формулу в предваренной нормальной форме, выводимо
эквивалентную формуле  . В каком классе
она окажется? (Указание: возможны разные варианты.)
. В каком классе
она окажется? (Указание: возможны разные варианты.)
108. Применим описанный метод к общезначимой формуле 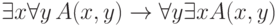 . Какая
предваренная формула получится? (Естественно, она будет
общезначимой.)
. Какая
предваренная формула получится? (Естественно, она будет
общезначимой.)
