Теорема Эрбрана

Сколемовские функции

В этом разделе мы в разных формах используем ровно одну идею: утверждение

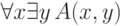
равносильно существованию функции, которая по любому дает такой , что 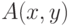. Это утверждение нельзя записать в виде эквивалентности поскольку в нашем языке нет квантора по функциям и мы писать не имеем права. (Языки, содержащие кванторы по множествам и функциям, называются языками второго порядка и мы их не рассматриваем.)

Тем не менее это утверждение можно сформулировать и в наших терминах. Пусть, например, имеется формула с двумя параметрами и . Тогда замкнутая формула 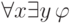выполнима тогда и только тогда, когда выполнима формула 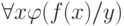, где — новый одноместный функциональный символ. (Аккуратный читатель поправит: надо еще требовать, чтобы подстановка вместо была корректна. Мы уже знаем, что переменные можно переименовывать, поэтому будем легкомысленно считать, что все необходимые переименования уже сделаны.)

Аналогичное преобразование выполнимо и для произвольных предваренных формул. Например, формула

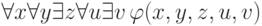
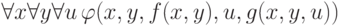
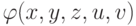выполнима тогда и только тогда, когда выполнима формула (здесь — формула, не имеющая параметров, кроме 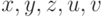, запись 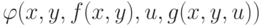обозначает результат соответствующих подстановок, которые мы предполагаем корректными, а и — функциональные символы, не встречающиеся в формуле ).

Сходное преобразование имеют в виду преподаватели математического анализа, которые иногда записывают определение предела ( ) в несколько странной для логика форме 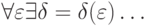— имеется в виду, что если для каждого найдется , то это самое представляет собой функцию от .

Отметим, что это рассуждение использует аксиому выбора, когда из различных возможных (для данного ) значений мы выбираем какое-то одно и объявляем его значением функции .

109. Казалось бы, выбор в приведенном выше примере зависит от 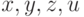, так что следовало бы написать 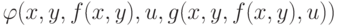— но мы так не делаем. Почему это допустимо?

Используя описанное преобразование, мы приходим к такой теореме:

Теорема 56. Для всякой замкнутой формулы сигнатуры можно указать формулу 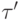класса сигнатуры с добавленными функциональными символами, которая выполнима или невыполнима одновременно с формулой . При этом преобразование эффективно (выполняется некоторым алгоритмом).

Приведя к предваренной нормальной форме, получим доказуемо эквивалентную формулу (выполнимую или невыполнимую одновременно с ). После этого применяем описанное выше преобразование.

Формула невыполнима тогда и только тогда, когда ее отрицание общезначимо. Поэтому наши рассуждения показывают, что, скажем, формула 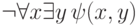общезначима одновременно с формулой . Внося отрицание внутрь и заменяя на , получаем такое утверждение: формулы

одновременно общезначимы. (Это утверждение чуть менее наглядно, чем двойственное ему утверждение о выполнимости.) В общем виде двойственное к теореме 56 утверждение выглядит так:

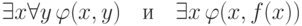
Теорема 57. Для всякой замкнутой формулы сигнатуры можно указать формулу 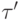класса 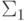сигнатуры с добавленными функциональными символами, которая общезначима или необщезначима одновременно с формулой . При этом преобразование эффективно (выполняется некоторым алгоритмом).

Заметим, что к формуле 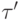можно применить теорему Эрбрана: она общезначима тогда и только тогда, когда дизъюнкция нескольких подстановок является тавтологией.

Теорема о полноте позволяет заменить в этой формулировке общезначимость на выводимость: формулы и 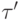одновременно выводимы. После этого естественно искать явный метод, который преобразует вывод формулы в вывод формулы 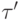и обратно. Такой метод действительно существует, но для этого требуется более детальный анализ структуры выводов, при котором удобно пользоваться исчислениями генценовского типа.

Идея использования функций вместо групп кванторов 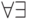восходит к Эрбрану и Сколему. Такие функции иногда называют "эрбрановскими" или "сколемовскими", а их добавление — "сколемизацией". Есть также термин "сколемовская нормальная форма", но здесь добавляются не функциональные символы, а предикатные, и получается формула не класса 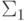, как в теореме 57, а класса .

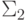Теорема 57 (о сколемовской нормальной форме). Для всякой замкнутой формулы сигнатуры можно указать формулу 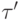класса 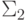сигнатуры с добавленными предикатными символами, которая общезначима или необщезначима одновременно с формулой . При этом преобразование эффективно (выполняется некоторым алгоритмом).

Как и раньше, нам будет удобнее говорить о выполнимости и доказывать, что для всякой формулы найдется одновременно с ней выполнимая формула 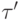из класса 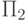. Построение такой формулы мы объясним на примере. Пусть исходная формула имеет вид

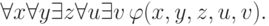
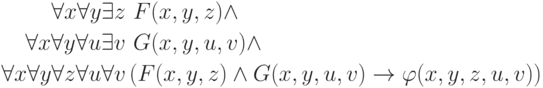
Мы теперь не можем ввести функции и , как это делалось выше. Поэтому мы введем предикаты и , заменяющие графики этих функций, и напишем формулу Если исходная формула выполнима, то новая тоже выполнима: достаточно взять в качестве и графики сколемовских функций. Напротив, если новая формула выполнима, то выполнима и старая (более того, из новой формулы следует старая): надо взять и согласно первым двум строкам и заметить, что согласно третьей строке они подойдут.

Такая конструкция применима к любой предваренной форме и дает конъюнкцию 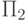-формул (последняя из которых будет даже и -формулой). А мы знаем, что такая конъюнкция эквивалентна 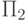-формуле.

110. Дайте синтаксическое доказательство теоремы о сколемовской нормальной форме (показав, что из выводимости формулы следует выводимость ее сколемовской нормальной формы и наоборот). (Указание: это проще, чем для формул с функциональными символами, и не требуется использовать генценовское исчисление.)

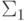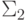Утверждения этого раздела сводят вопрос о выводимости произвольной формулы исчисления предикатов к выводимости -формулы (с функциональными символами). Если мы запрещаем функциональные символы, то вопрос о выводимости произвольной формулы сводится к выводимости - формулы.

Известно (теорема Черча, доказательство можно прочесть в [5]), что вопрос о выводимости произвольных формул языка первого порядка неразрешим: не существует алгоритма, который бы по произвольной замкнутой формуле определял бы, выводима она или нет. Результаты этого раздела показывают, что уже для формул класса 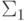(с функциональными символами) или 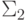(без них) такого алгоритма не существует, поскольку из него можно было бы получить и общий алгоритм. 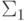(В предыдущем разделе мы видели, что для формул класса без функциональных символов такой алгоритм существует.)