Теорема Эрбрана
Теорема Эрбрана
Естественно ожидать, что вопрос о выводимости (или
общезначимости) формулы тем сложнее, чем сложнее сама формула. В
этом разделе (а также в следующем) мы рассмотрим его для формул
класса  и
и 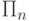 .
.
Начнем с самого простого случая — бескванторных формул. Пусть  — бескванторная формула. Посмотрим, из каких атомарных
формул она составлена, и заменим их на пропозициональные
переменные (разные — на разные, одинаковые — на одинаковые).
Получится формула логики высказываний, которую мы будем называть
прототипом формулы
— бескванторная формула. Посмотрим, из каких атомарных
формул она составлена, и заменим их на пропозициональные
переменные (разные — на разные, одинаковые — на одинаковые).
Получится формула логики высказываний, которую мы будем называть
прототипом формулы  . Имеет место следующее (почти
очевидное) утверждение.
. Имеет место следующее (почти
очевидное) утверждение.
Теорема 54 (выводимость бескванторных формул). Бескванторная формула выводима (общезначима) тогда и только тогда, когда ее прототип является тавтологией.
Если прототип формулы  является тавтологией, то
формула
является тавтологией, то
формула  является частным случаем пропозициональной
тавтологии и потому выводима и общезначима.
является частным случаем пропозициональной
тавтологии и потому выводима и общезначима.
Пусть прототип формулы  не является тавтологией. Можно
считать, что формула
не является тавтологией. Можно
считать, что формула  замкнута, поскольку свободные
переменные с точки зрения общезначимости и выводимости ничем не
отличаются от констант (мы уже отмечали это при доказательстве
теоремы о полноте). Построим интерпретацию, где формула
замкнута, поскольку свободные
переменные с точки зрения общезначимости и выводимости ничем не
отличаются от констант (мы уже отмечали это при доказательстве
теоремы о полноте). Построим интерпретацию, где формула  будет ложной. Носителем ее будут замкнутые термы.
Значения предикатов мы подберем так, чтобы атомарные формулы
принимали те самые значения, которые делают прототип
формулы
будет ложной. Носителем ее будут замкнутые термы.
Значения предикатов мы подберем так, чтобы атомарные формулы
принимали те самые значения, которые делают прототип
формулы  ложным. Это возможно, так как значения
разных атомарных формул можно выбирать независимо (это значения
либо разных предикатов, либо одного и того же предиката, но на
разных термах).
ложным. Это возможно, так как значения
разных атомарных формул можно выбирать независимо (это значения
либо разных предикатов, либо одного и того же предиката, но на
разных термах).
Что можно сказать про общезначимость формул классов  и
и 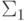 ? Для класса
? Для класса  все просто:
общезначимость формулы со свободными переменными равносильна общезначимости ее
замыкания (которое получается, если навесить кванторы
всеобщности по всем переменным), поэтому формулы класса
все просто:
общезначимость формулы со свободными переменными равносильна общезначимости ее
замыкания (которое получается, если навесить кванторы
всеобщности по всем переменным), поэтому формулы класса  по существу ничем не отличаются от бескванторных.
по существу ничем не отличаются от бескванторных.
Вопрос для класса 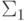 решается следующей теоремой:
решается следующей теоремой:
Теорема 55 (Эрбрана). Формула 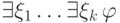 (где
формула
(где
формула  — бескванторная) общезначима тогда и только
тогда, когда найдется конечный список подстановок
— бескванторная) общезначима тогда и только
тогда, когда найдется конечный список подстановок
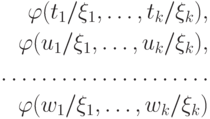
Заметим, что дизъюнкция, о которой идет речь в теореме, является бескванторной формулой. По теореме 54 она общезначима тогда и только тогда, когда является частным случае пропозициональной тавтологии.
Прежде чем доказывать эту теорему, приведем пример. Рассмотрим формулу

 и
и  — константы). Она общезначима;
соответствующий набор состоит из подстановок
— константы). Она общезначима;
соответствующий набор состоит из подстановок 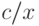 и
и 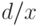 . В самом
деле, формула
. В самом
деле, формула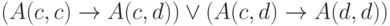
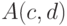 , так и при ложном.
Заметим, что в этом примере нам понадобились две подстановки.
, так и при ложном.
Заметим, что в этом примере нам понадобились две подстановки.Доказательство теоремы Эрбрана. В одну сторону утверждение очевидно: если общезначима дизъюнкция подстановок, то общезначима формула с квантором. (Мы уже использовали это при элиминации кванторов в разделе "Элиминация кванторов" при доказательстве теоремы 28.)
Докажем обратное утверждение. Будем считать, что
формула  не содержит переменных,
кроме
не содержит переменных,
кроме 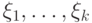 (как мы уже замечали, остальные
переменные можно заменить константами). Рассмотрим (бесконечное)
множество формул
(как мы уже замечали, остальные
переменные можно заменить константами). Рассмотрим (бесконечное)
множество формул
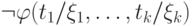
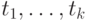 . Если
это множество противоречиво, все доказано (тогда выводима
дизъюнкция подстановок, отрицания которых
используются при выводе противоречия). Если оно
непротиворечиво, то существует интерпретация, в которой все эти
формулы истинны. Мы не можем утверждать, что в этой интерпретации
ложна формула
. Если
это множество противоречиво, все доказано (тогда выводима
дизъюнкция подстановок, отрицания которых
используются при выводе противоречия). Если оно
непротиворечиво, то существует интерпретация, в которой все эти
формулы истинны. Мы не можем утверждать, что в этой интерпретации
ложна формула
Заметим, что теорему Эрбрана можно сформулировать чисто
синтаксически: если выводима 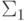 -формула
-формула  , то можно найти конечное число
подстановок, дизъюнкция которых выводима. Можно предложить и
доказательство, не использующее понятия общезначимости. Такое доказательство приведено, например, в книге
Клини [16] (для генценовского
варианта исчисления предикатов) и в книге Шенфилда
[31] (для гильбертовского варианта). Синтаксическое доказательство (в
отличие от нашего) конструктивно: по выводу
, то можно найти конечное число
подстановок, дизъюнкция которых выводима. Можно предложить и
доказательство, не использующее понятия общезначимости. Такое доказательство приведено, например, в книге
Клини [16] (для генценовского
варианта исчисления предикатов) и в книге Шенфилда
[31] (для гильбертовского варианта). Синтаксическое доказательство (в
отличие от нашего) конструктивно: по выводу 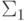 -формулы
можно алгоритмически указать соответствующие термы.
-формулы
можно алгоритмически указать соответствующие термы.
Если сигнатура не содержит функциональных символов, то теорема
Эрбрана позволяет алгоритмически проверить выводимость формул
класса 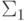 , поскольку число возможных подстановок
конечно. Это же можно сказать и про формулы класса
, поскольку число возможных подстановок
конечно. Это же можно сказать и про формулы класса 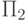 , так
как внешние кванторы всеобщности можно отбросить, не меняя
выводимости.
, так
как внешние кванторы всеобщности можно отбросить, не меняя
выводимости.
Естественный вопрос: можно ли построить аналогичные алгоритмы для следующих классов? Отрицательный ответ дается в следующем разделе.
