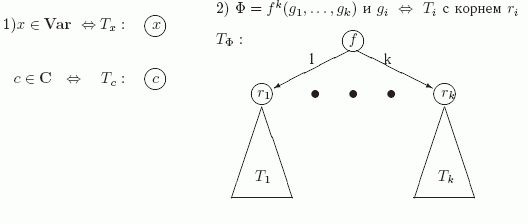Деревья

Деревья и формулы (выражения)

Напомним, что в "Индукция и комбинаторика" было введено общее понятие формулы над системой функций 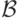(определение 3.2), которое применимо для произвольных функций, а не только булевых. В "Эквивалентность формул и нормальные формы" аналогичные синтаксические объекты для логики предикатов названы термами (определение 7.1), а в языках программирования такие конструкции часто называются выражениями.

Итак, пусть формула над множеством функций , множеством констант C и множеством переменных Var определяется индуктивно по следующим правилам.

• Переменная из Var есть формула.
• Константа из C есть формула.
• Если g₁, ..., g_k - формулы, а f^(k) - k -местная функция из F, то f(g₁, ..., g_k) - это формула.

Обозначим множество всех таких формул через .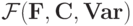

Рассмотрим класс упорядоченных размеченных деревьев 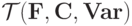, листья которых помечены элементами из 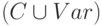, а внутренние вершины - функциями из F, причем, если вершина помечена символом k -местной функции из F, то у нее имеется k сыновей.

Рис. 10.3. Индуктивное определение связи между формулами и деревьями

Предложение 10.1. Между множеством формул\ 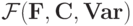и множеством деревьев 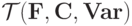имеется взаимно однозначное соответствие.

Доказательство Это соответствие легко устанавливается индукцией по определениям формул и деревьев. Оно показано выше на рис. 10.3.

Пример 10.2. Рассмотрим, например, класс обычных арифметических формул над множеством функций F = { +, -, *, : }, целочисленных констант C = {0, 1, 2,... } и переменных Var = {x,y,z, ... }. Пусть формула 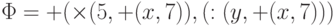(ее обычное представление )

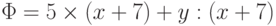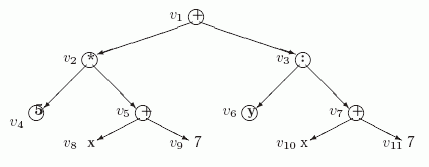
Тогда в соответствии с предложением 10.1 эта формула представляется деревом 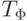, изображенном на рис. 10.4.

Рис. 10.4. Дерево T

На этом рисунке не указаны явно номера ребер, выходящих из внутренних вершин дерева, которые идентифицируют порядок аргументов операций. Предполагается, что для коммутативных операций +, * это несущественно, а для некоммутативных, таких, как :, первый аргумент расположен левее второго.

Заметим, что у деревьев, представляющих арифметические или логические (булевские) формулы, внутренние вершины имеют не более 2-х сыновей. Такие деревья образуют важный подкласс ориентированных деревев, называемых бинарными или двоичными.

Определение 10.4. Ориентированное дерево называется бинарным или двоичным, если у каждой его внутренней вершины имеется не более двух сыновей, причем ребра, ведущие к ним помечены двумя разными метками (обычно используются метки из пар: "левый" - "правый", 0 - 1, + - - и т.п.)

Бинарное дерево называется полным, если у каждой его внутренней вершины имеется два сына и все его ветви имеют одинаковую длину.

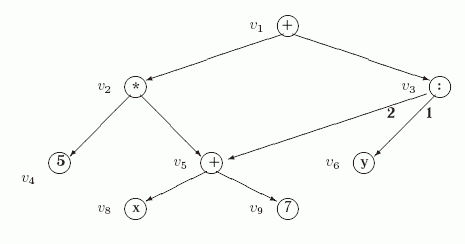
Ориентированные ациклические графы также используются для представления формул. Они получаются из соответствующих деревьев при склеивании вершин, представляющих одинаковые подформулы. Для формулы 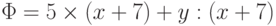такой граф 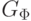получается при склеивании вершин v₅ и v₇ дерева 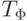, представляющих подформулу (x+7).

Рис. 10.5. Ациклический граф G

На рис.10.5 явно указаны номера ребер, выходящих из вершины v₃, которые определяют порядок аргументов приписанной этой вершине операции :. Ясно, что при отсутствии такого указания и использовании порядка " по умолчанию" - первый аргумент слева - граф представлял бы другое выражение.