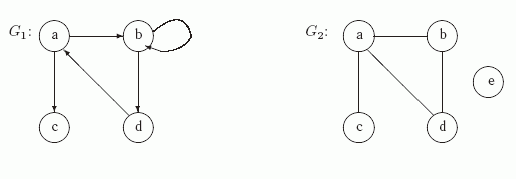|
Это в лекции 3. |
Графы: представления, достижимость и связность
Основные понятия
Мы часто сталкиваемся с задачами, в условиях которых заданы некоторые объекты и между некоторыми их парами имеются определенные связи. Если объекты изобразить точками ( вершинам и), а связи - линиями ( ребрами ), соединяющими соответствующие пары точек, то получится рисунок, называемый графом. Историю теории графов принято исчислять с 1736 г., когда Эйлер исследовал "задачу о кенигсберских мостах": построить в графе циклический путь, проходящий по одному разу через каждое ребро. В середине 19-го века Гамильтон заинтересовался задачей построения циклического пути, проходящего по одному разу через каждую вершину графа1Интересно, что несмотря на внешнюю похожесть задача Эйлера имеет простое эффективное решение (см. задачу 11.1), а задача Гамильтона в общем случае эффективно не решается. К тому же времени относится использование графов для анализа электрических цепей ( Кирхгоф ) и химических молекул (Кэли). Развитие современной теории графов относится к 30-м годам 20-го столетия. Они нашли многочисленные применения в электротехнике, электронике, биологии, экономике, программировании и в других областях. В этой и двух следующих лекциях мы рассмотрим основные понятия теории графов и несколько широко используемых в различных приложениях типовых задач, таких, как представления графов, отношение достижимости и транзитивное замыкание графа, компоненты сильной связности ориентированного графа и его базы, деревья и их обходы, минимальные остовные деревья, поиск в глубину и поиск кратчайших путей. Основное внимание уделено алгоритмическим процедурам, решающим указанные задачи.
Приведем основные определения.
Определение 9.1. Ориентированный граф - это пара (V, E), где V - конечное множество вершин (узлов, точек) графа, а E - некоторое множество пар вершин, т.е. подмножество множества V x V или бинарное отношение на V. Элементы E называют ребрами (дугами, стрелками, связями). Для ребра 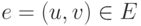 вершина u называется началом e, а вершина v - концом e, говорят, что ребро e ведет из u в v.
вершина u называется началом e, а вершина v - концом e, говорят, что ребро e ведет из u в v.
Неориентированный граф G=(V, E) - это ориентированный граф, у которого для каждого ребра 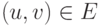 имеется противоположное ребро
имеется противоположное ребро 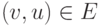 , т.е. отношение E симметрично. Такая пара (u,v), (v,u) называется неориентированным ребром. Для его задания можно использовать обозначение для множества концов: {u, v}, но чаще используется указание одной из пар в круглых скобках. Если
, т.е. отношение E симметрично. Такая пара (u,v), (v,u) называется неориентированным ребром. Для его задания можно использовать обозначение для множества концов: {u, v}, но чаще используется указание одной из пар в круглых скобках. Если 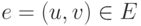 ,
то вершины u и v называются смежными в G, а ребро e и эти вершины называются инцидентными.
Степенью вершины в неориентированном графе называется число смежных с ней вершин. Вершина степени 0 называется изолированной.
,
то вершины u и v называются смежными в G, а ребро e и эти вершины называются инцидентными.
Степенью вершины в неориентированном графе называется число смежных с ней вершин. Вершина степени 0 называется изолированной.
В ориентированном графе полустепень исхода вершины - это число исходящих из нее ребер, а полустепень захода - это число входящих в данную вершину ребер.
Заметим, что в ориентированном графе может быть ребро вида (u,u), называемое петлей, а в неориентированном петель не бывает.
Пример 9.2. На рис.9.1 приведены примеры ориентированного графа G1=(V1, E1) и не ориентированного графа G2=(V2, E2). Здесь V1={ a,b,c,d}, E1={ (a,b), (a,c), (b,b), (b,d), (d,a)}, V2={ a,b,c,d}, E2={ (a,b), (a,c), (a,d), (b,d)}. В графе G1 ребро (b,b) является петлей, полустепень исхода вершины a равна 2, а полустепень захода для нее равна 1. В графе G2 степень вершины a равна 3, вершин b и d - 2, вершины c - 1, а вершины e - 0, т.е. вершина e является изолированной,
Во многих приложениях с вершинам и и ребрами графов связывается некоторая дополнительная информация. Обычно она представляется с помощью функций разметки вершин и ребер.
Определение 9.2. Размеченный граф - это ориентированный или неориентированный граф G= (V, E), снабженный одной или двумя функциями разметки вида: l: V -> M и c: E -> L, где M и L - множества меток вершин и ребер, соответственно.
Упорядоченный граф -
это размеченный граф G= (V, E), в котором ребра, выходящие из
каждой вершины 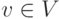 , упорядочены, т.е. помечены номерами 1, ..., kv, где kv -
полустепень исхода v, т.е.
, упорядочены, т.е. помечены номерами 1, ..., kv, где kv -
полустепень исхода v, т.е. 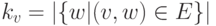 .
.
В качестве множества меток ребер L часто выступают числа, задающие "веса", "длины", "стоимости" ребер. Графы с такой разметкой часто называют взвешенными.
Во многих случаях естественно не различать графы, отличающиеся лишь именами (порядком) вершин.
Определение 9.3. Изоморфизм графов. Два графа G1= (V1, E1) и G2= (V2, E2) называются изоморфными,
если между их вершинам и существует взаимно однозначное соответствие 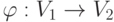 такое, что для любой пары вершин u, v из V1 ребро
такое, что для любой пары вершин u, v из V1 ребро 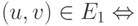 ребро
ребро 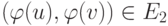 .
.
Для изоморфизма размеченных графов требуется также совпадение
меток соответствующих вершин : 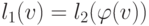 и/или ребер:
и/или ребер: 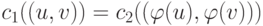 .
.
Многие приложения графов связаны с изучением путей между их вершинами.
Определение 9.4. Путь в ориентированном или неориентированном графе - это последовательность
ребер вида (v1,v2),(v2,v3), ... , (vn-1,vn). Этот путь ведет из начальной вершины v1 в конечную вершину vn
и имеет длину n-1. В этом случае будем говорить, что vn достижима из v1.
Будем считать, что каждая вершина достижима сама из себя путем длины 0. Путь можно также определять как соответствующую
последовательность вершин: (v1,v2,v3, ... , vn-1,vn), где 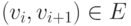 при i=1,2,..., n-1.
при i=1,2,..., n-1.
Путь назывется простым, если все ребра и все вершины на нем, кроме, быть может, первой и последней, различны.
Циклом в ориентированном графе называется путь, в котором начальная вершина совпадает с конечной и который содержит хотя бы одно ребро. Цикл (v1,v2, ... , v_{n-1},vn=v1) называется простым, если в нем нет одинаковых вершин, кроме первой и последней, т.е. если все вершины v2, ... , v_{n-1} различны.
В неориентированном графе путь (v1,v2, ... , vn-1,vn=v1) называется циклом, если n >= 4 и все ребра (vi, vi+1) различны.
Если в графе нет циклов, то он называется ациклическим.
Из последнего определения следует, что длина цикла в неориентированном графе не меньше 3. Следующее утверждение непосредственно следует из определений.
Лемма 9.1. Если в графе G ( ориентированном или неориентированном ) имеется путь из u в v, то в нем имеется и простой путь из u в v.
Неориентированный граф называется связным, если любая пара вершин в нем соединена путем. При выполнении такого же условия ориентированный граф называется сильно связным.
Представления графов
Из определения графа следует, что каждый граф G=(V,E) можно задать, непосредственно перечислив его множество вершин V и множество ребер E. Однако такое представление неудобно для решения многих задач о графах. Например, чтобы проверить наличие ребра между двумя вершинам и, придется, вообще говоря, просмотреть все множество E. Хорошее представление, по крайней мере, должно позволить легко переходить от вершины к ее соседу и перечислять всех ее соседей.
В этом параграфе мы рассмотрим три разных способа представления графов, которые более эффективны при решении типичных для теории графов задач.