Квантовый аналог NP: класс BQNP
Утверждение 13.3. Задача локальный гамильтониан полна в классе BQNP относительно полиномиальной сводимости.
Идея доказательства восходит к Фейнману [29]: замена унитарной эволюции не зависящим от времени гамильтонианом (т.е. переход от схемы к локальному гамильтониану).
Доказательство. Итак, пусть есть схема размера  :
:  . Будем считать, что
. Будем считать, что  действует на пространстве из
действует на пространстве из  q-битов, первые
q-битов, первые  из которых — q-биты подсказки, а остальные — вспомогательные (взятые напрокат на время вычислений); считаем также, что схема состоит из операторов, действующих на парах q-битов.
из которых — q-биты подсказки, а остальные — вспомогательные (взятые напрокат на время вычислений); считаем также, что схема состоит из операторов, действующих на парах q-битов.
Гамильтониан, сопоставляемый схеме. Он действует на пространстве

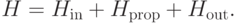
Слагаемое 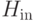 отвечает начальному состоянию и равно
отвечает начальному состоянию и равно
 |
( 13.8) |
 — проектор на подпространство векторов, у которых
— проектор на подпространство векторов, у которых  -й бит равен
-й бит равен  . Второй сомножитель в этой формуле действует в пространстве счетчика.
. Второй сомножитель в этой формуле действует в пространстве счетчика.Слагаемое  отвечает конечному состоянию и равно
отвечает конечному состоянию и равно
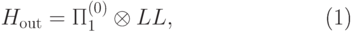 |
( 13.9) |
И, наконец, слагаемое  описывает эволюцию системы и состоит, как и следовало ожидать, из
описывает эволюцию системы и состоит, как и следовало ожидать, из  слагаемых, каждое из которых отвечает за переход от
слагаемых, каждое из которых отвечает за переход от 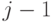 к
к  :
:
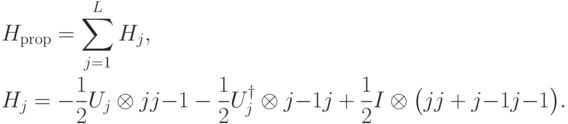 |
( 13.10) |
Каждое слагаемое 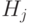 действует на два q-бита из пространства состояний и на q-биты пространства счетчика.
действует на два q-бита из пространства состояний и на q-биты пространства счетчика.
Замена базиса. Произведем замену базиса, задаваемую оператором

 — измеряющий оператор: измеряется значение счетчика
— измеряющий оператор: измеряется значение счетчика  и к q-битам пространства состояний схемы применяется оператор эволюции за время
и к q-битам пространства состояний схемы применяется оператор эволюции за время  .
.Гамильтониан при такой замене изменится на сопряженный: 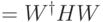 . Посмотрим, как действует сопряжение оператором
. Посмотрим, как действует сопряжение оператором  на слагаемые
на слагаемые  .
.
На слагаемое 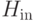 сопряжение не влияет:
сопряжение не влияет:
 |
( 13.11) |
Действие на слагаемое  :
:
 |
( 13.12) |
Слагаемое 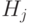 состоит из трех. Вначале запишем действие сопряжения на первое из слагаемых в (13.10):
состоит из трех. Вначале запишем действие сопряжения на первое из слагаемых в (13.10):

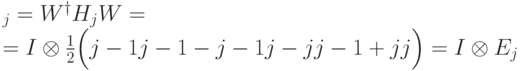
 |
( 13.13) |
Оценка собственного числа при ответе "да". Предположим, что схема, на вход которой подан вектор 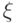 , дает ответ 1 с вероятностью не меньше, чем
, дает ответ 1 с вероятностью не меньше, чем 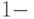 . Это, по определению, означает, что
. Это, по определению, означает, что

Докажем, что в этом случае у  (а, значит, и у
(а, значит, и у  ) есть малое собственное число. Для этого предъявим такой вектор
) есть малое собственное число. Для этого предъявим такой вектор  , что
, что 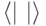 достаточно мало (минимум квадратичной формы
достаточно мало (минимум квадратичной формы 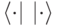 достигается на собственном векторе).
достигается на собственном векторе).
В пространстве счетчика выберем вектор
 |
( 13.14) |
 равен
равен  . Оценим
. Оценим 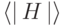 .
.Очевидно, что 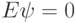 . Поэтому
. Поэтому
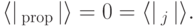
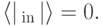

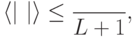
 есть собственное число с такой же верхней оценкой.
есть собственное число с такой же верхней оценкой.Оценка собственного числа при ответе "нет". В этом случае нам нужно доказать, что все собственные числа велики. Пусть для любого вектора 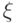 вероятность ответа 1 не превосходит
вероятность ответа 1 не превосходит 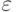 , т.е.
, т.е.
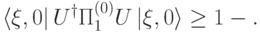
 больше либо равны
больше либо равны 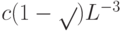 , где
, где  — некоторая константа.
— некоторая константа.Доказательство довольно длинное, поэтому вначале приведем его краткий план. Представив гамильтониан в виде суммы  операторов
операторов  и
и 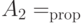 , мы оценим снизу наименьшие ненулевые собственные числа
, мы оценим снизу наименьшие ненулевые собственные числа 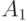 и
и 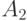 по отдельности. Получим оценки
по отдельности. Получим оценки  и
и 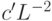 соответственно. Чтобы оценить наименьшее собственное число
соответственно. Чтобы оценить наименьшее собственное число  , нам потребуется лемма, которая дает такую оценку для суммы через оценки для слагаемых и угол между их нулевыми подпространствами. Углом между подпространствами
, нам потребуется лемма, которая дает такую оценку для суммы через оценки для слагаемых и угол между их нулевыми подпространствами. Углом между подпространствами  и
и 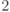 с нулевым пересечением будем называть величину
с нулевым пересечением будем называть величину 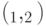 , задаваемую условиями
, задаваемую условиями
![\begin{equation}\label{уголопр} \cos\vt(\calL_1,\calL_2)=\mkern-2mu\max\limits_{\begin{array}{l} \scriptstyle\ket{\eta_1}\in \calL_1\\[-2pt] \scriptstyle\ket{\eta_2}\in \calL_2\end{array}}\mkern-2mu \big|\langle \eta_1\ket{\eta_2}\big|,\qquad 0<\vt(\calL_1,\calL_2)<\frac{\pi}{2}. \end{equation}](/sites/default/files/tex_cache/f4a1690e43a81c1c7c45b102f34e6b3e.png) |
( 13.15) |

