НОУ ИНТУИТ | Классические и квантовые вычисления. Лекция 7: Базисы для квантовых схем

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Московский государственный университет имени М.В.Ломоносова

Опубликован: 15.03.2007 | Доступ: свободный | Студентов: 616 / 27 | Оценка: 5.00 / 4.50 | Длительность: 19:30:00

Тема: Алгоритмы и дискретные структуры

Специальности: Программист

|

Вам нравится? Нравится 11 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Приближенная реализация.

Теперь перейдем к конечным базисам. В этом случае возможно только приближенное представление операторов произведениями базисных. Чтобы определить приближенную реализацию, нам потребуется норма на пространстве операторов.

На пространстве состояний есть норма $\big\| |\xi\rangle \big\| = \sqrt{\langle \xi|\xi\rangle }$ . Она, как и любая норма, по определению удовлетворяет следующим условиям:

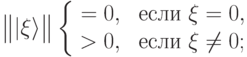$\big\| |\xi\rangle \big\| &\left\{\begin{array}{rl} =0,& \mbox{ если } \ket\xi=0,\\ >0,& \mbox{ если } \ket\xi\ne 0;\\ \end{array}\right.\\$

( 7.3)

( 7.4)

$\big\| c|\xi\rangle \big\|&= |c| \big\| |\xi\rangle \big\|.$

( 7.5)

Введем теперь норму на пространстве операторов. Пусть $\calN$ — пространство с нормой. Пространство операторов, действующих на нем, можно представить как $\LL(\calN)=\calN\otimes\calN^*$ (изоморфизм задается матричным представлением $\sum_{}^{}a_{jk}\ket{j}\bra{k}$ ).

Определение 7.2. Норма оператора (так называемая операторная норма\, вообще говоря, есть и другие) равна

$\|X\|\ =\ \sup_{|\xi\rangle\not=0} \frac{\big\|X |\xi\rangle\big\|}{\big\| |\xi\rangle\big\|}.$

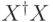Заметим, что $\|X\|^2$ — наибольшее собственное число оператора $X^\dagger X$ .

Эта норма обладает всеми перечисленными выше свойствами нормы, а кроме того, еще несколькими специфическими:

$\| XY\|&\leq \|X\|\, \|Y\|;\label{опнорм1}$

( 7.6)

$\|X^\dagger\|&=\| X\|; \label{опнорм2}$

( 7.7)

$\| X\otimes Y\|&=\|X\|\, \|Y\|, & \text{где } & X\in\LL(\calN),\Y\in\LL(\calM).\label{опнорм3}$

( 7.8)

Доказательства этих свойств нормы получаются непосредственно из определения и оставляются в качестве упражнения.

Дадим теперь определение приближенной реализуемости. Если искомый оператор — , то его приближенная реализация будет обозначаться $\tilde U$ .

Определение 7.3. Оператор $\tilde U$ представляет оператор с точностью $\delta$ , если $\| \tilde U-U\|\le\delta$ .

У этого определения есть два замечательных свойства. Во-первых, если мы имеем произведение нескольких операторов $U= U_L\cdot\ldots\cdot U_2U_1$ , каждый из которых имеет свое приближение $\tilde U_k$ с точностью $\delta_k$ , то произведение этих приближений $\tilde U= \tilde U_L\cdot\ldots\cdot \tilde U_2\tilde U_1$ приближает с точностью $\sum_{}^{}\delta_k$ ( ошибки накапливаются линейно ):

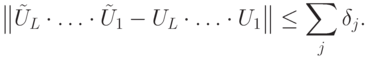
$\big\| \tilde U_L\cdot\ldots\cdot\tilde U_1 - U_L\cdot\ldots\cdot U_1\big\|\le\sum_{j}^{}\delta_j .$

Достаточно рассмотреть пример с двумя операторами:

$\begin{multline*} \| \tilde U_2 \tilde U_1 -U_2U_1\|= \|\tilde U_2(\tilde U_1-U_1)+(\tilde U_2-U_2)U_1\|\leq\\ \leq \|\tilde U_2(\tilde U_1-U_1)\|+\|(\tilde U_2-U_2)U_1\| \leq \|\tilde U_2\|\, \|(\tilde U_1-U_1)\|+\|(\tilde U_2-U_2)\|\,\|U_1\|= \\ = \|(\tilde U_1-U_1)\|+\|(\tilde U_2-U_2)\|. \end{multline*}$

В этой выкладке последнее равенство справедливо благодаря унитарности операторов. (Если рассматривать неунитарные операторы, то ошибки приближения могут накапливаться гораздо быстрее, например, экспоненциально.)

Замечание 7.1. Всякая модель, претендующая на решение сложных задач какими-то реальными физическими процессами, должна обязательно изучаться на предмет устойчивости к ошибкам приближения. (В реальной жизни параметры любого физического процесса можно задать лишь с некоторой точностью.) В частности, вычисление с экспоненциальным накоплением ошибок почти заведомо бесполезно с практической точки зрения.

Второе свойство понятия " $\tilde U$ представляет с точностью $\delta$ " мы сформулируем в более общем контексте.

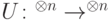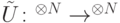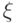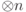Определение 7.4. Оператор $U\colon\BB^{\otimes n} \to\BB^{\otimes n}$ приближается в расширенном смысле оператором $\tilde U\colon\BB^{\otimes N} \to\BB^{\otimes N}$ с точностью $\delta$ , если для любого $\ket\xi$ из $\BB^{\otimes n}$ выполнено

$\big\|\tilde U\left(\ket\xi\otimes\ket{0^{N-n}}\right)- U\ket\xi\otimes\ket{0^{N-n}}\big\|\le\delta \big\| \ket\xi\big\|.$

( 7.9)

Сформулируем это определение еще одним способом. Введем оператор $V\colon\BB^{\otimes n}\to \BB^{\otimes N}$ , который действует по правилу $V\colon\ket\xi\mapsto \ket\xi\double\otimes\ket{0^{N-n}}$ . Оператор не унитарный, но изометричный. Условие из последнего определения можно переписать так

$\| \tilde UV-VU\|\le\delta.$

( 7.10)

Рассуждение про накопление ошибок проходит и в этом случае (что, конечно, следует проверить).

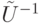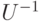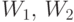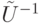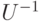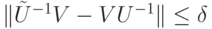Справедливо следующее утверждение: если $\tilde U$ приближает (в расширенном смысле) с точностью $\delta$ , то $\tilde U^{-1}$ приближает $U^{-1}$ с той же точностью $\delta$ . Это следует из того, что $\| W_1XW_2\|=\|X\|$ для унитарных операторов $W_1,\, W_2$ . Умножая выражение под нормой в (7.10) слева на $\tilde U^{-1}$ , а справа — на $U^{-1}$ , получим следствие из неравенства (7.10): $\| \tilde U^{-1}V-VU^{-1}\|\le\delta$ .

Определение 7.5. Будем называть базис $\calA$ полным, если любой унитарный оператор можно с любой точностью представить в расширенном смысле квантовой схемой в базисе $\calA$ .

Теорема 7.2. (см. [4]). Базис $\calQ=\{H,K,\QXOR,\Lambda^2(\sx)\}$ , где

$H\ =\ \frac{1}{\sqrt{2}} \leftp\begin{array}{rr} 1&1\\ 1&-1 \end{array} \rightp, \qquad K\ =\ \leftp\begin{array}{cc} 1&0\\ 0&\ii \end{array} \rightp,$

является полным. (Такой базис будем называть стандартным.)

Доказательство этой теоремы следует из решения задач 7.5-7.9.

Замечание 7.2. Если убрать из базиса $\calQ$ квантовый элемент Тоффоли, он перестает быть полным. Однако многие важные вычисления можно делать и в таком усеченном базисе. В частности, как будет видно в дальнейшем, схемы, исправляющие ошибки, можно реализовать без элемента Тоффоли.

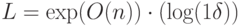Можно оценить сложность реализации оператора в этом базисе. Если $U\colon{} \BB^{\otimes n}\to\BB^{\otimes n}$ , то можно реализовать этот оператор с точностью $\delta$ квантовой схемой в базисе $\calQ$ размера $L=\exp(O(n))\cdot \poly(\log(\slashfrac{1}{\delta}))$ . Если матричные элементы заданы в двоичной записи, то эта схема строится по с помощью некоторого алгоритма примерно за то же время (множители и степени полинома могут отличаться). Идея построения такого алгоритма легко усматривается из задач 7.1 и 7.11.

Задачи

Докажите, что все операторы на одном q-бите в сочетании с оператором $\Lambda(\sx)$ образуют полный базис. Решение должно быть достаточно эффективным: должен существовать алгоритм, который строит схему, реализующую произвольный оператор на q-битах, за время $\exp(O(n))\cdot \poly(\log(1/\delta))$ .
Докажите свойства операторной нормы(7.6-7.8).
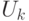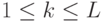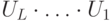Пусть операторы $\tilde U_k$ приближают в расширенном смысле операторы с точностью $\delta_k$ , $1\leq k\leq L$ . Докажите, что оператор $\tilde U_L\cdot\ldots\cdot \tilde U_1$ приближает в расширенном смысле оператор $U_L\cdot\ldots\cdot U_1$ с точностью $\sum_{}^{}\delta_k$ .
Пусть оператор $\tilde U$ приближает в расширенном смысле оператор с точностью $\delta$ . Докажите, что существует оператор , точно представляющий в расширенном смысле, т.е. выполняется равенство
$W\left(\ket\xi\otimes\ket{0^{N-n}}\right)= (U\ket\xi)\otimes\ket{0^{N-n}},$
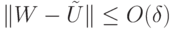и такой, что $\|W-\tilde U\|\le O(\delta)$ .
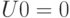Пусть унитарный оператор $U\colon{} \BB^{\otimes n} \to \BB^{\otimes n}$ удовлетворяет условию $U\ket0=\ket0$ . Постройте реализующую 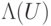$\Lambda(U)$ схему размера 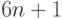в базисе $\calQ\cup\{U\}$ , использующую оператор один раз.
Пусть — некоммутирующие элементы группы $\SO(3)$ — повороты на углы, несоизмеримые с $\pi$ . Докажите, что группа, порожденная и , образует всюду плотное подмножество в $\SO(3)$ .
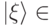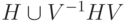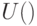Пусть $\calM$ — унитарное пространство размерности $\ge 3$ . Рассмотрим подгруппу $H\subset\U(\calM)$ — стабилизатор одномерного подпространства, порожденного некоторым единичным вектором $|\xi\rangle\in\calM$ . Пусть — произвольный унитарный оператор, не сохраняющий подпространство $\CC(|\xi\rangle)$ . Докажите, что множество операторов $H\cup V^{-1}HV$ порождает всю группу $U(\calM)$ .

(Заметим, что в условии этой задачи 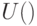$U(\calM)$ и можно профакторизовать по подгруппе фазовых сдвигов ).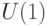
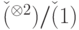Докажите, что операторы из стандартного базиса порождают всюду плотное множество в $\U(\BB^{\otimes2})/\U(1)$ .
Докажите, что фазовые сдвиги можно реализовать в стандартном базисе, используя напрокат дополнительные q-биты.
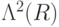Докажите, что отрицание $\sx$ и элемент Дойча $\Lambda^2(R)$ , где $R=-i\exp(\pi i\alpha\sx)$ , $\alpha$ — иррациональное, образуют полный базис для квантового вычисления.
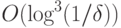Докажите, что любой оператор , действующий на одном q-бите, может быть приближенно реализован в расширенном смысле с точностью $\delta$ схемой размера $O(\log^3(1/\delta))$ в стандартном базисе, и есть полиномиальный алгоритм построения этой схемы по описанию .

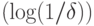Эта задача довольно сложна, к ее решению лучше приступать после знакомства с разделами 11 и 12 и решения задачи 12.3 (квантовое преобразование Фурье). Предлагаемый путь решения является достаточно изощренным. В статье [4] был использован более прямой (но тоже неочевидный) подход, при котором получается схема размера $\poly(\log(1/\delta))$ .