Что такое алгоритм?
Схемы
Схема (булева) — это способ вычислить функцию  . Помимо исходных переменных
. Помимо исходных переменных  , для которых вычисляется значение
, для которых вычисляется значение  , схема использует некоторое количество вспомогательных переменных
, схема использует некоторое количество вспомогательных переменных 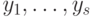 и некоторый набор ( базис ) булевых (т.е. принимающих значения 0 или 1) функций
и некоторый набор ( базис ) булевых (т.е. принимающих значения 0 или 1) функций 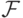 . Схема
. Схема  в базисе
в базисе 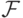 определяется последовательностью присваиваний
определяется последовательностью присваиваний 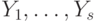 . Каждое присваивание
. Каждое присваивание  имеет вид
имеет вид 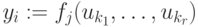 , где
, где 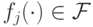 , а переменная
, а переменная 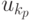 (
( 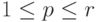 ) — это либо одна из исходных переменных
) — это либо одна из исходных переменных 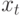 (
( 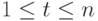 ), либо вспомогательная переменная
), либо вспомогательная переменная  с меньшим номером (
с меньшим номером ( 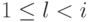 ). Таким образом, для каждого набора значений исходных переменных последовательное выполнение присваиваний, входящих в схему, однозначно определяет значения всех вспомогательных переменных. Результатом вычисления считаются значения последних
). Таким образом, для каждого набора значений исходных переменных последовательное выполнение присваиваний, входящих в схему, однозначно определяет значения всех вспомогательных переменных. Результатом вычисления считаются значения последних  переменных
переменных 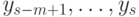 .
.
Схема вычисляет функцию  , если для любых значений
, если для любых значений  исходных переменных результатом вычисления является
исходных переменных результатом вычисления является 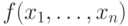 .
.
Схема называется формулой, если каждая вспомогательная переменная используется в правой части присваиваний только один раз. (Обычные математические формулы именно так задают последовательность присваиваний: "внутри" формул не принято использовать ссылки на их части или другие формулы.)
Схему можно также представлять в виде ориентированного ациклического графа, у которого вершины входной степени 0 ( входы ) помечены исходными переменными; остальные вершины ( функциональные элементы ) помечены функциями из базиса (при этом входная степень вершины должна совпадать с количеством аргументов ее пометки); ребра помечены числами, указывающими номера аргументов; вершины выходной степени 0 ( выходы ) помечены переменными, описывающими результат работы схемы. Вычисление на графе определяется индуктивно: как только известны значения всех вершин 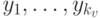 , из которых ведут ребра в данную вершину
, из которых ведут ребра в данную вершину  , вершина
, вершина  получает значение
получает значение 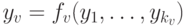 , где
, где 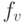 — базисная функция, которой помечена вершина. При переходе к графу схемы мы опускаем несущественные присваивания, которые ни разу не используются на пути к выходным вершинам, так что они никак не влияют на результат вычисления.
— базисная функция, которой помечена вершина. При переходе к графу схемы мы опускаем несущественные присваивания, которые ни разу не используются на пути к выходным вершинам, так что они никак не влияют на результат вычисления.
Базис называется полным, если для любой булевой функции  есть схема в этом базисе, вычисляющая
есть схема в этом базисе, вычисляющая  . Ясно, что в полном базисе можно вычислить произвольную функцию
. Ясно, что в полном базисе можно вычислить произвольную функцию 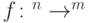 (такую функцию можно представить как упорядоченный набор из
(такую функцию можно представить как упорядоченный набор из  булевых функций).
булевых функций).
Булева функция может быть задана таблицей значений. Приведем таблицы значений для трех функций
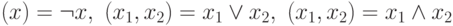
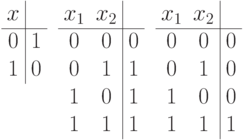
Конъюнкция и дизъюнкция определяются для произвольного числа булевых переменных аналогичным образом: конъюнкция равна 1 только тогда, когда все аргументы равны 1, а дизъюнкция равна 0 только тогда, когда все аргументы равны 0. В стандартном базисе они очевидным образом вычисляются схемами (и даже формулами) размера 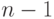 .
.
Теорема 1.1. Базис 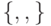 — полный.
— полный.
Доказательство. Литералом будем называть переменную или ее отрицание. Конъюнкцией литералов (это схема и даже формула) легко представить функцию  , которая принимает значение 1 ровно один раз: при
, которая принимает значение 1 ровно один раз: при 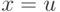 . Если
. Если 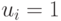 , включаем в конъюнкцию переменную
, включаем в конъюнкцию переменную  , если
, если 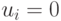 , то включаем в конъюнкцию
, то включаем в конъюнкцию  . Произвольная функция
. Произвольная функция  может быть представлена в виде
может быть представлена в виде
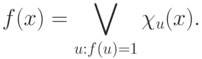 |
( 1.1) |
В таком случае говорят, что  представлена в дизъюнктивной нормальной форме (ДНФ), т.е. как дизъюнкция конъюнкций литералов2Далее нам еще потребуется и конъюнктивная нормальная форма (КНФ) — конъюнкция дизъюнкций литералов.
Как уже говорилось, дизъюнкция нескольких переменных выражается формулой в стандартном базисе.
представлена в дизъюнктивной нормальной форме (ДНФ), т.е. как дизъюнкция конъюнкций литералов2Далее нам еще потребуется и конъюнктивная нормальная форма (КНФ) — конъюнкция дизъюнкций литералов.
Как уже говорилось, дизъюнкция нескольких переменных выражается формулой в стандартном базисе.
Размером схемы называется количество присваиваний в схеме. Минимальный размер схемы в базисе 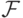 , вычисляющей функцию
, вычисляющей функцию  , называется схемной сложностью функции
, называется схемной сложностью функции  в базисе
в базисе 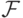 и обозначается
и обозначается  . Переход от одного полного конечного базиса к другому полному конечному базису меняет схемную сложность функций на множитель
. Переход от одного полного конечного базиса к другому полному конечному базису меняет схемную сложность функций на множитель 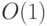 . Так что в асимптотических оценках выбор конкретного полного базиса неважен и поэтому будем использовать обозначение
. Так что в асимптотических оценках выбор конкретного полного базиса неважен и поэтому будем использовать обозначение 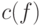 для схемной сложности
для схемной сложности  в конечном полном базисе.
в конечном полном базисе.
Каждый предикат  на множестве
на множестве  определяет последовательность булевых функций
определяет последовательность булевых функций 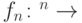 следующим образом:
следующим образом:  , где справа стоит характеристическая функция предиката
, где справа стоит характеристическая функция предиката  .
.
Определение 1.5. Предикат  принадлежит классу
принадлежит классу  , если
, если 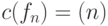 .
.
Теорема 1.2. 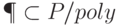 .
.
Если МТ работает за полиномиальное время, то и память, которую она использует, ограничена полиномом. Поэтому весь процесс вычисления на входном слове  длины
длины  можно представить таблицей вычисления размера
можно представить таблицей вычисления размера  , где
, где  ,
, 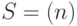 .
.
Строка с номером  таблицы задает состояние МТ после
таблицы задает состояние МТ после  тактов работы. Символы
тактов работы. Символы 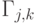 , записанные в таблице, принадлежат алфавиту
, записанные в таблице, принадлежат алфавиту 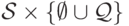 . Символ
. Символ 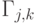 определяет пару (символ, записанный в
определяет пару (символ, записанный в  -й ячейке после
-й ячейке после  тактов работы; состояние управляющего устройства после
тактов работы; состояние управляющего устройства после  тактов работы, если головка находится над
тактов работы, если головка находится над  -й ячейкой, в противном случае второй элемент пары —
-й ячейкой, в противном случае второй элемент пары —  ). Для простоты также считаем, что если вычисление заканчивается при некотором входе за
). Для простоты также считаем, что если вычисление заканчивается при некотором входе за  тактов, то строки c номерами, большими
тактов, то строки c номерами, большими 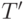 , повторяют строку с номером
, повторяют строку с номером 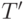 .
.
Построить схему, вычисляющую значения предиката на словах длины  , можно следующим образом. Состояние каждой клетки таблицы можно закодировать конечным (не зависящим от
, можно следующим образом. Состояние каждой клетки таблицы можно закодировать конечным (не зависящим от  ) числом булевых переменных. Имеются локальные правила согласования, т.е. состояние каждой клетки
) числом булевых переменных. Имеются локальные правила согласования, т.е. состояние каждой клетки  в строке ниже нулевой однозначно определяется состояниями клеток в предыдущей строке, лежащих непосредственно над данной (
в строке ниже нулевой однозначно определяется состояниями клеток в предыдущей строке, лежащих непосредственно над данной (  ), левее данной (
), левее данной ( 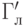 ) и правее данной (
) и правее данной ( 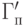 ). Каждая переменная, кодирующая состояние клетки
). Каждая переменная, кодирующая состояние клетки  , есть функция от переменных, кодирующих состояния клеток
, есть функция от переменных, кодирующих состояния клеток 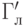 ,
,  ,
, 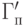 . Все эти функции могут быть вычислены схемами конечного размера. Объединяя эти схемы, получим схему, вычисляющую все переменные, кодирующие состояния клеток таблицы; размер этой схемы будет
. Все эти функции могут быть вычислены схемами конечного размера. Объединяя эти схемы, получим схему, вычисляющую все переменные, кодирующие состояния клеток таблицы; размер этой схемы будет  .
.
Осталось заметить, что переменные, кодирующие часть клеток нулевой строки, определяются входным словом, а переменные, кодирующие остальные клетки нулевой строки, являются константами. Чтобы узнать результат вычисления, нужно определить символ, записанный в нулевой ячейке ленты в конце вычисления. Без ограничения общности можно считать, что состояния клеток таблицы кодируются так, что одна из кодирующих переменных равна 1 только в том случае, когда в ячейке записана 1. Тогда значение этой переменной для кода 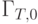 и будет результатом вычисления.
и будет результатом вычисления.
Замечание 1.1. Класс  шире класса
шире класса  . Любой функции от натурального аргумента
. Любой функции от натурального аргумента  со значениями в
со значениями в  можно сопоставить предикат
можно сопоставить предикат 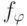 по правилу
по правилу  , где
, где 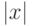 обозначает длину слова
обозначает длину слова  . Ограничение такого предиката на слова длины
. Ограничение такого предиката на слова длины  тождественно равно 0 или 1 (в зависимости от
тождественно равно 0 или 1 (в зависимости от  ). Схемная сложность таких функций ограничена константой. Поэтому все такие предикаты по определению принадлежат P/poly, хотя среди них есть и неразрешимые предикаты.
). Схемная сложность таких функций ограничена константой. Поэтому все такие предикаты по определению принадлежат P/poly, хотя среди них есть и неразрешимые предикаты.
Справедливо следующее усиление теоремы.
Теорема 1.3.  принадлежит
принадлежит 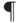 тогда и только тогда, когда
тогда и только тогда, когда

- существует МТ, которая по числу
 за время
за время  строит схему вычисления
строит схему вычисления 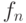 .
.
Доказательство.  Данное в доказательстве теоремы 1.2. описание нетрудно превратить в МТ, которая строит схему вычисления
Данное в доказательстве теоремы 1.2. описание нетрудно превратить в МТ, которая строит схему вычисления 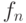 за полиномиальное по
за полиномиальное по  время (схема
время (схема 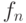 имеет простую структуру: каждая переменная связана с предыдущими одними и теми же правилами согласования).
имеет простую структуру: каждая переменная связана с предыдущими одними и теми же правилами согласования).
 Столь же просто. Вычисляем размер входного слова. Затем строим по этому размеру схему
Столь же просто. Вычисляем размер входного слова. Затем строим по этому размеру схему 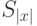 вычисления
вычисления 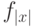 , используя указанную в условии 2 машину. После этого вычисляем
, используя указанную в условии 2 машину. После этого вычисляем 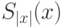 на машине, которая по описанию схемы и значениям входных переменных вычисляет значение схемы за полиномиальное от длины входа время.
на машине, которая по описанию схемы и значениям входных переменных вычисляет значение схемы за полиномиальное от длины входа время.

