|
Пожалуйста, проясните ситуацию. Был выбран курс " Компьютерная алгебра" для самостоятельного изучения. Как теперь записаться на этот курс с целью получения диплома о повышении квалификации? На данный момент он имеет статус " изучаю". Если я пройду экзаменационный тест в таком статусе без оформления документов и оплаты диплома, придется ли еще раз регистрироваться на этот курс и заново проходить тестирование? |
Проблема представления данных
3.8. УПРАЖНЕНИЯ.
- Любое кольцо можно рассматривать как разностное кольцо с тождественным изоморфизмом.
- Кольцо многочленов R[x] от одной переменной над обыкновенным разностным кольцом можно превратить в обыкновенное разностное кольцо, произвольным образом задав
значение
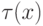 . Показать, что значением
. Показать, что значением 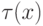 трансляция
кольца R[x] определяется однозначно.
трансляция
кольца R[x] определяется однозначно. - Показать, что не любой автоморфизм
 кольца R[x] продолжается на кольцо формальных степенных рядов.
кольца R[x] продолжается на кольцо формальных степенных рядов. - Пусть R - разностное кольцо без делителей нуля, F - его поле частных. Показать, что F можно единственным образом превратить в разностное поле, содержащее разностное кольцо R.
- Поле формальных (сходящихся) рядов Лорана K((x)) можно рассматривать как обыкновенное разностное поле с оператором трансляции
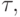 таким, что
таким, что  , где k —
произвольный ненулевой элемент поля K.
, где k —
произвольный ненулевой элемент поля K.
3.9. ОПРЕДЕЛЕНИЕ. Пусть R — разностное кольцо с множеством
операторов трансляции  Под разностным модулем над R, или разностным R - модулем, мы понимаем R -модуль M, на котором
действуют операторы из множества
Под разностным модулем над R, или разностным R - модулем, мы понимаем R -модуль M, на котором
действуют операторы из множества  в соответствии со следующими условиями
в соответствии со следующими условиями

Разностный модуль M можно рассматривать как левый модуль
над кольцом косых многочленов ![R[\Delta] = R[\tau_1,\dots,\tau_n]](/sites/default/files/tex_cache/26f2f9805b7ad02ec8f15c719d8e52b7.png) разностного
типа. Это кольцо мы будем называть кольцом разностных операторов. Пусть T — свободная коммутативная полугруппа (записываемая мультипликативно), порожденная элементами множества
разностного
типа. Это кольцо мы будем называть кольцом разностных операторов. Пусть T — свободная коммутативная полугруппа (записываемая мультипликативно), порожденная элементами множества  Каждый элемент кольца
Каждый элемент кольца ![R[\Delta ]](/sites/default/files/tex_cache/751d17ecc66fad16ef653f0d9452fdc2.png) может быть единственным образом
записан в виде конечной суммы
может быть единственным образом
записан в виде конечной суммы
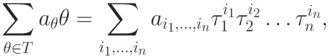
умножение образующих задается соотношениями
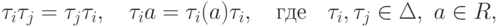
и по линейности распространяется на все кольцо ![R[\Delta ]](/sites/default/files/tex_cache/751d17ecc66fad16ef653f0d9452fdc2.png) . Это кольцо иногда называют кольцом разностных многочленов, но мы будем придерживаться терминологии, принятой в монографии
[
18
]
,
где кольцом разностных многочленов над разностным кольцом R
называют разностное кольцо
. Это кольцо иногда называют кольцом разностных многочленов, но мы будем придерживаться терминологии, принятой в монографии
[
18
]
,
где кольцом разностных многочленов над разностным кольцом R
называют разностное кольцо 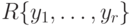 многочленов от счетного множества неизвестных
многочленов от счетного множества неизвестных 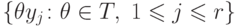 над R. В кольце
над R. В кольце 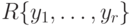 операторы трансляции из множества
операторы трансляции из множества  действуют на
коэффициентах по определению разностного кольца, а на образующих
действуют на
коэффициентах по определению разностного кольца, а на образующих 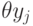 — по правилу:
— по правилу: 
3.10. УПРАЖНЕНИЯ. Пусть F — обыкновенное разностное поле с
автоморфизмом 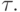 Доказать следующие свойства кольца
Доказать следующие свойства кольца ![R = F[\tau ]](/sites/default/files/tex_cache/0f87aae0f1011a9595b6f67368f4f924.png) линейных разностных операторов над F:
линейных разностных операторов над F:
- в R нет делителей нуля;
- R является кольцом главных левых (правых, двусторонних) идеалов;
- в R нет нетривиальных двусторонних идеалов;
- в R имеется алгоритм Евклида для нахождения левого (правого) НОД двух операторов;
- в R имеется алгоритм Евклида для нахождения левого (правого) НОД двух операторов;
- R не обязательно является кольцом с однозначным разложением на множители (привести пример разностного поля F, для которого это свойство не выполняется).
Кольца дифференциальных и разностных многочленов с точки зрения теории колец представляют собой кольца коммутативных многочленов от счетного множества переменных (каждый конкретный многочлен зависит только от конечного числа переменных). Таким образом, для решения задачи представления данных в кольце дифференциальных (разностных) многочленов и поле рациональных дифференциальных (разностных) функций достаточно упорядочить кольцевые образующие. Кольцо дифференциальных многочленов является дифференциальным кольцом, т. е. наряду с операциями сложения и умножения в нем имеются унарные операции дифференцирования, переводящие кольцевую образующую в другую кольцевую образующую, и отношение порядка на множестве кольцевых образующих выбирается так, чтобы оно было согласовано с дифференцированиями. Аналогично, кольцо разностных многочленов является разностным кольцом.
Векторные пространства и модули.
В вычислительной математике и в алгебре понятие векторного пространства над некоторым полем K играет ключевую роль. При фиксированном базисе пространства задача представления данных не представляет какой-либо сложности — два вектора совпадают тогда и только тогда, когда совпадают все их координаты в фиксированном базисе. Соответствующая структура данных — вектор элементов типа K с индексом 1..n — является одной из базисных структур данных в программировании. Для случая, когда коэффициенты образуют кольцо R, не являющееся полем, положение существенно сложнее — аналогом понятия векторного пространства (множество, замкнутое относительно сложения, вычитания и умножения на элементы кольца с естественными аксиомами сложения и умножения) является в этом случае понятие модуля. Важным частным случаем модуля является свободный модуль над кольцом R ( R -модуль). В частности, любое кольцо с единицей можно рассматривать как свободный модуль над самим собой, любой идеал кольца является его подмодулем. С точки зрения задачи представления данных соответствующая структура данных такж может быть при фиксированном базисе описана как вектор элементов типа R с индексом 1..n.
С другой стороны, свободный модуль над алгеброй обобщенных многочленов можно рассматривать как бесконечномерное векторное пространство над основным полем. В качестве базиса этого пространства удобно выбрать всевозможные произведения мономов из кольца обобщенных многочленов на модульные образующие. Любой элемент модуля содержится в некотором конечномерном подпространстве, порожденном каким-то подмножеством базисных векторов. Выбор базисных векторов и отношения порядка на множестве базисных векторов определяет каноническую форму любого элемента свободного модуля над кольцом обобщенных многочленов.
К сожалению, множество свободных модулей незамкнуто относительно модульных гомоморфизмов, т. е. как подмодули, так и фактормодули свободного модуля не обязаны быть свободными модулями.
3.11. УПРАЖНЕНИЯ.
- Привести пример идеала в кольце многочленов от двух переменных, не являющегося свободным модулем над этим кольцом.
- Привести пример факторкольца кольца многочленов от одной переменной, не являющегося свободным модулем над этим кольцом.
