|
Пожалуйста, проясните ситуацию. Был выбран курс " Компьютерная алгебра" для самостоятельного изучения. Как теперь записаться на этот курс с целью получения диплома о повышении квалификации? На данный момент он имеет статус " изучаю". Если я пройду экзаменационный тест в таком статусе без оформления документов и оплаты диплома, придется ли еще раз регистрироваться на этот курс и заново проходить тестирование? |
Проблема представления данных
Обобщенные многочлены и рациональные функции.
В дифференциальной алгебре имеется ряд объектов, которые можно рассматривать как обобщение кольца многочленов. К ним относятся алгебры Вейля, кольца дифференциальных операторов и кольца дифференциальных многочленов. Строгое определение колец дифференциальных операторов и колец дифференциальных многочленов будет дано ниже, здесь отметим только, что элементы алгебры Вейля или кольца дифференциальных операторов могут быть представлены в виде суммы одночленов от фиксированного конечного множества переменных с коэффициентами из фиксированного поля, т. е. так же, как и элементы кольца многочленов (допускается как плотная, так и разреженная запись). Сложности вычислений в таких кольцах связаны с некоммутативностью умножения. Некоммутативность умножения особенно сказывается при рассмотрении тел частных для этих колец (существование их доказывается в курсах по теории колец): правое частное двух элементов может не совпадать с их левым частным, правые множители отличаются от левых множителей, приходится рассматривать правые и левые наибольшие общие делители и наименьшие общие кратные, которые для взаимно простых элементов не совпадают с их произведениями.
В этом параграфе приводятся основные определения и результаты из дифференциальной и разностной алгебры, которые понадобятся нам в дальнейшем.
3.2. ОПРЕДЕЛЕНИЕ. Оператор 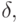 действующий на некотором кольце, называется оператором дифференцирования (или просто дифференцированием), если
действующий на некотором кольце, называется оператором дифференцирования (или просто дифференцированием), если  и
и 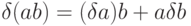 для всех элементов a, b этого кольца. Дифференциальным кольцом называется коммутативное кольцо R с конечным множеством
для всех элементов a, b этого кольца. Дифференциальным кольцом называется коммутативное кольцо R с конечным множеством 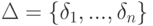 операторов дифференцирования кольца R, таких,
что
операторов дифференцирования кольца R, таких,
что 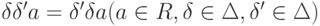 ; если n = 1, то дифференциальное кольцо R называется обыкновенным, если n > 1, то R называется кольцом с частными производными. Если кольцо R
является полем, то мы говорим о дифференциальном поле.
; если n = 1, то дифференциальное кольцо R называется обыкновенным, если n > 1, то R называется кольцом с частными производными. Если кольцо R
является полем, то мы говорим о дифференциальном поле.
- Показать, что любое кольцо можно рассматривать как дифференциальное кольцо с нулевым дифференцированием. Показать, что на кольцах
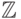 ,
,  ,
, 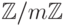 нет ненулевых дифференцирований.
нет ненулевых дифференцирований. - Кольцо многочленов R[x] от одной переменной над обыкновенным дифференциальным кольцом можно превратить
в обыкновенное дифференциальное кольцо, произвольным
образом задав значение
 . Показать, что значением
. Показать, что значением  продолжение дифференцирования
продолжение дифференцирования  на кольцо R[x] определяется однозначно. Аналогичное утверждение верно для
кольца формальных степенных рядов.
на кольцо R[x] определяется однозначно. Аналогичное утверждение верно для
кольца формальных степенных рядов. - Пусть R — дифференциальное кольцо без делителей нуля, F — его поле частных. Показать, что F можно единственным образом превратить в дифференциальное поле, содержащее дифференциальное кольцо R.
- Поле мероморфных в некоторой области вещественного n -
мерного пространства функций можно рассматривать как
дифференциальное поле, с множеством дифференцирований
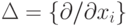
ОПРЕДЕЛЕНИЕ. Пусть R — дифференциальное кольцо с множеством операторов дифференцирования  Под дифференциальным модулем над R или дифференциальным R -модулем мы понимаем R -модуль M, на котором действуют операторы множества
Под дифференциальным модулем над R или дифференциальным R -модулем мы понимаем R -модуль M, на котором действуют операторы множества  в соответствии со следующими правилами:
в соответствии со следующими правилами:
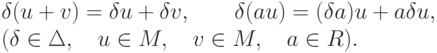
Дифференциальный модуль можно рассматривать как левый модуль над кольцом косых многочленов ![R[\Delta]=R[\delta_1,\dots,\delta_n]](/sites/default/files/tex_cache/89a480127cea416fce63d5ede720e099.png) дифференциального типа. Это кольцо мы будем называть кольцом линейных дифференциальных операторов. Пусть T обозначает свободную коммутативную полугруппу (записанную мультипликативно),
порожденную элементами из множества
дифференциального типа. Это кольцо мы будем называть кольцом линейных дифференциальных операторов. Пусть T обозначает свободную коммутативную полугруппу (записанную мультипликативно),
порожденную элементами из множества  Каждый элемент кольца
Каждый элемент кольца ![R[\Delta ]](/sites/default/files/tex_cache/751d17ecc66fad16ef653f0d9452fdc2.png) может быть единственным способом выражен в виде конечной
суммы
может быть единственным способом выражен в виде конечной
суммы
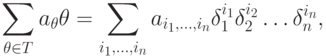
умножение образующих определяется правилами:

В предположении, что для кольца коэффициентов R каноническое представление фиксировано, каноническое представление кольца дифференциальных операторов ![R[\Delta ]](/sites/default/files/tex_cache/751d17ecc66fad16ef653f0d9452fdc2.png) получается так же, как и для кольца многочленов: достаточно упорядочить полугруппу T.
Обычно рассматриваются отношения порядка, перечисленные в параграфе 3.1.
получается так же, как и для кольца многочленов: достаточно упорядочить полугруппу T.
Обычно рассматриваются отношения порядка, перечисленные в параграфе 3.1.
3.5. ПРИМЕР. Пусть R — кольцо многочленов над полем K, R = K[x1, . . . , xm], и 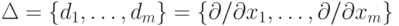 . Тогда
кольцо линейных дифференциальных операторов
. Тогда
кольцо линейных дифференциальных операторов ![R[\Delta ]](/sites/default/files/tex_cache/751d17ecc66fad16ef653f0d9452fdc2.png) называется
алгеброй Вейля над K и обозначается Am(K).
называется
алгеброй Вейля над K и обозначается Am(K).
Кольцо линейных дифференциальных операторов обладает многими свойствами, аналогичными свойствам кольца многочленов, в частности, если кольцо коэффициентов является дифференциальным полем, то в кольце дифференциальных операторов нет делителей нуля, для любых двух элементов существует наибольший общий
делитель (правый или левый, причем в общем случае они не совпадают) и наименьшее общее кратное (правое и левое, снова не совпадающие); если  -поле, то в
-поле, то в ![F[\delta ]](/sites/default/files/tex_cache/080bcf01eb8b23bbb063e2702df8fadb.png) имеется алгоритм Евклида
для нахождения левого (правого) наибольшего общего делителя.
имеется алгоритм Евклида
для нахождения левого (правого) наибольшего общего делителя.
3.6. УПРАЖНЕНИЯ. Пусть F — обыкновенное дифференциальное
поле с дифференцированием 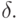 Доказать следующие свойства кольца
Доказать следующие свойства кольца ![R = F[\delta ]](/sites/default/files/tex_cache/4a99600b80d64b2feb100aca69e4b080.png) линейных дифференциальных операторов над F:
линейных дифференциальных операторов над F:
- в R нет делителей нуля;
- R является кольцом главных левых (правых) идеалов;
- в R нет нетривиальных двусторонних идеалов;
- в R имеется алгоритм Евклида для нахождения левого (правого) НОД двух операторов;
- в R имеется расширенный алгоритм Евклида для нахождения левого (правого) НОД двух операторов;
- R не обязательно является кольцом с однозначным разложением на множители (привести пример дифференциального поля F, для которого это свойство не выполняется).
Кольцо ![R[\Delta ]](/sites/default/files/tex_cache/751d17ecc66fad16ef653f0d9452fdc2.png) иногда называют кольцом дифференциальных многочленов, но мы будем придерживаться терминологии, принятой в
монографии
[
23
]
, где кольцом дифференциальных многочленов над
дифференциальным кольцом R называется кольцо R{y1, . . . , yr} многочленов от счетного множества переменных
иногда называют кольцом дифференциальных многочленов, но мы будем придерживаться терминологии, принятой в
монографии
[
23
]
, где кольцом дифференциальных многочленов над
дифференциальным кольцом R называется кольцо R{y1, . . . , yr} многочленов от счетного множества переменных 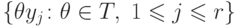 над кольцом R. В кольце R{y1, . . . , yr} операторы дифференцирования из множества
над кольцом R. В кольце R{y1, . . . , yr} операторы дифференцирования из множества  действуют на коэффициентах по определению дифференциального кольца, а на образующих
действуют на коэффициентах по определению дифференциального кольца, а на образующих 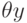 —по правилу:
—по правилу: 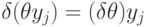 .
.
Кольцо дифференциальных многочленов с точки зрения теории колец представляет собой кольцо коммутативных многочленов от счетного множества переменных (каждый конкретный многочлен зависит только от конечного числа переменных). Таким образом, для решения задачи представления данных кольца дифференциальных многочленов и поля рациональных дифференциальных функций достаточно упорядочить кольцевые образующие. Кольцо дифференциальных многочленов является дифференциальным кольцом, т. е. наряду с операциями сложения и умножения в нем имеются унарные операции дифференцирования, переводящие кольцевую образующую в другую кольцевую образующую, отношение порядка на множестве кольцевых образующих выбирается так, чтобы оно было согласовано с дифференцированиями.
Аналогичные объекты — кольца разностных операторов и кольца разностных многочленов — рассматриваются в разностной алгебре. Кольцо разностных операторов отличается от кольца диф- ференциальных операторов коммутационными соотношениями, все сказанное выше о кольце дифференциальных операторов можно повторить и для кольца разностных операторов. В кольце разностных многочленов вместо операторов дифференцирования рассматриваются операторы трансляции, которые также переводят кольцевые образующие друг в друга, но на поле коэффициентов являются не дифференцированиями, а автоморфизмами (соответственно, для них можно рассматривать отрицательные степени).
3.7. ОПРЕДЕЛЕНИЕ. Разностное кольцо определяется как кольцо R с фиксированным конечным множеством 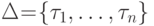 взаимно
коммутирующих мономорфизмов кольца R в себя. Если все мономорфизмы
взаимно
коммутирующих мономорфизмов кольца R в себя. Если все мономорфизмы 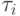 — изоморфизмы, то R называется инверсным разностным кольцом. Если n = 1, то R называется обыкновенным
разностным кольцом, в противном случае R называется кольцом с
частными разностями. Элементы множества
— изоморфизмы, то R называется инверсным разностным кольцом. Если n = 1, то R называется обыкновенным
разностным кольцом, в противном случае R называется кольцом с
частными разностями. Элементы множества  называются операторами трансляции.
называются операторами трансляции.
